双分子耦合的Schnakenberg模型的稳态系统解的先验估计*

杨彦思 ，刘 萍

(哈尔滨师范大学)

0 引言

Schnakenberg模型是用来描述具有可能振荡性质的自催化化学反应的基本微分方程模型.两种化学反应物X，Y和两种化学源物质A，B之间的化学反应形式是:

根据能量守恒定律，可以得出描述这一反应的化学物质X和Y的浓度u和v的两个反应扩散方程.方程的非量纲化形式为:

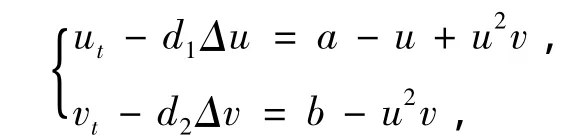
其中d1，d2是化学物质X，Y的扩散系数，a，b是A，B的浓度，我们假设A，B是充足的，也就a，b保持常量.四个方程的Schnakenberg模型是以两个方程的 Schnakenberg模型为基础的，Neumann边界条件下的四个方程的Schnakenberg模型为:

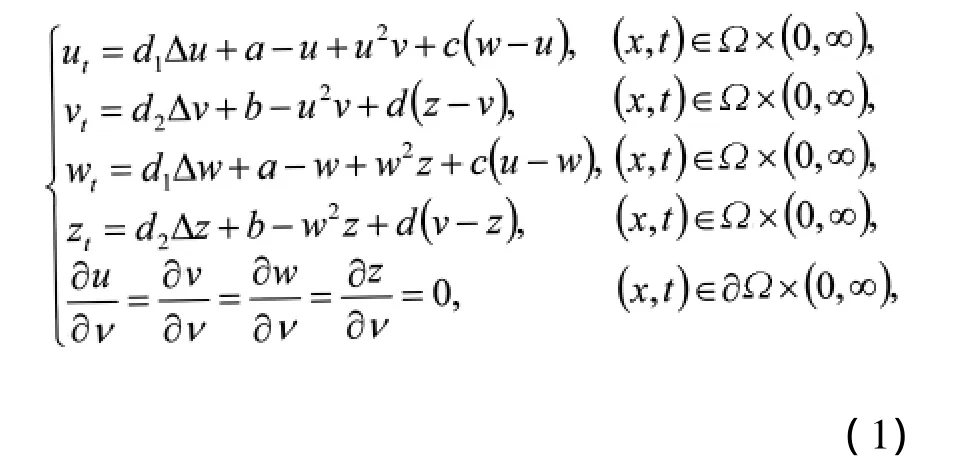
其中c表示u，w这两种化学物质在反应中分子间的移动速率，d表示v，z这两种化学物质在反应中分子间的移动速率，为了研究方便一般取d=0，即v，z这两种物质在反应中不发生分子间的移动.该系统比两个方程的Schnakenberg模型的结构复杂，但应用性更广，更适合于描述现实生活中的化学反应.

1 预备知识

(i)如果w∈C2(Ω)×C1()，满足

定理1.2 (Poincare不等式)令Ω是Rn中的一个有界连通开子集，且∂Ω是C1的，假设1≤p≤∞，则存在一个常数C=C(n，p，Ω)，使得对于每一u∈W1，p(Ω)有成立，其中

定理 1.3 (Holder不等式)假设1≤p，q≤，如果u∈Lp(Ω)，v∈Lq(Ω)则有

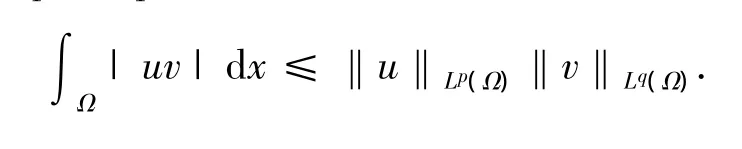
2 主要结果

系统(1)的稳态系统

解的一个先验估计.

定理2 系统(1)的任意解(u，v，w，z)满足估计

其中 ‖·‖1，2表示W1，2(Ω)范数，μ1为区域Ω内具有齐次Neumann边界条件的-Δ算子的第一个非零特征值.

证明 将系统(1)的第一个方程和第三个方程相加，得

即u+w满足

所以由定理1.1，设x0为u+w的极小值点，则有2a-(u+w)(x0)≤0，从而u+w≥2a，∀x∈.由系统(2.1)的第一个方程及w≥2a-u，得

所以u满足

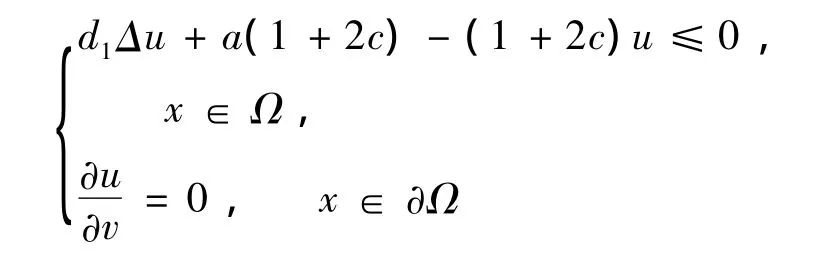
再次应用定理1.1，设x1为u的极小值点，则有a(1+2c)-(1+2c)u(x1)≤0，即u≥a.由于v满足

设x2为v的极大值点，则由定理1.1可知b-

u2(x2)v(x2)≥0，所以.同样地，重复上面的过程，我们可以得到w≥a，及

将系统(1)的第一个方程至第四个方程相加得

将上式在Ω上积分得

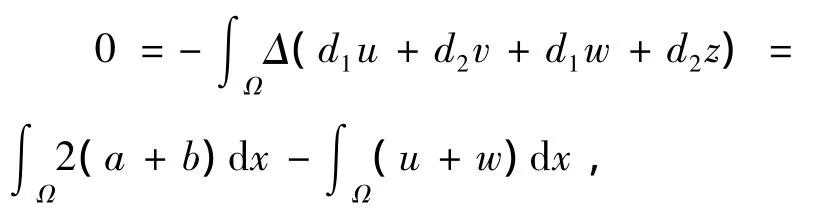
所以有

将系统(1)的第二个方程乘以v在Ω上积分得

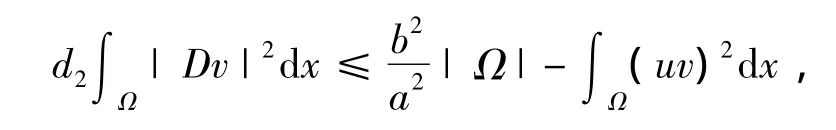
因此

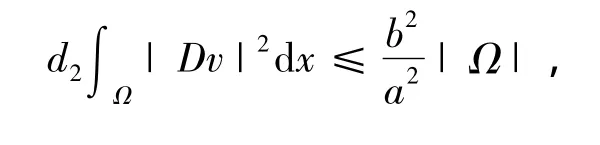
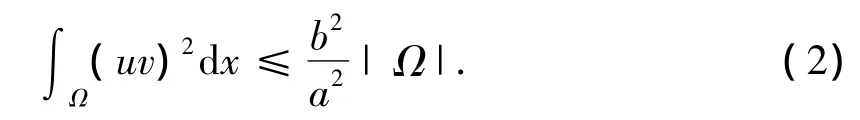
将系统(1)第四个方程乘以z在Ω上积分得

用u分别乘以系统(2)的第一个及第二个方程，w分别乘以系统(2)的第三个及第四个方程，并在Ω上积分得

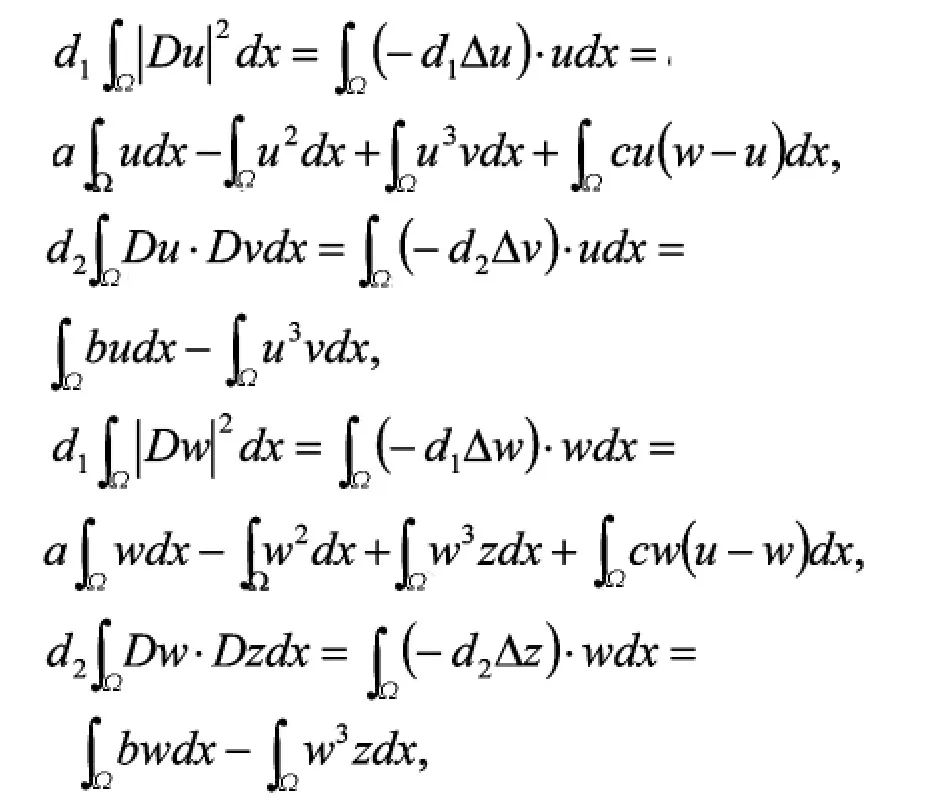
将上述四个方程左右两边分别相加，整理得

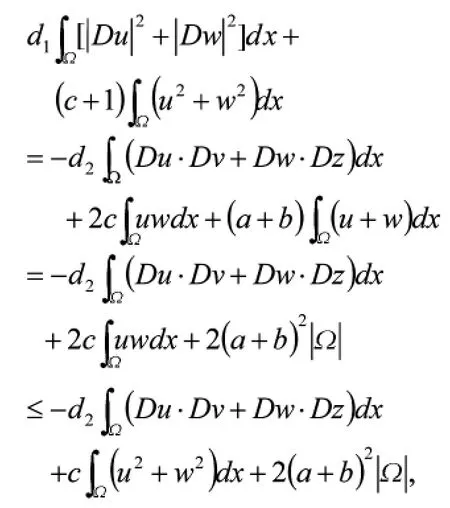
即

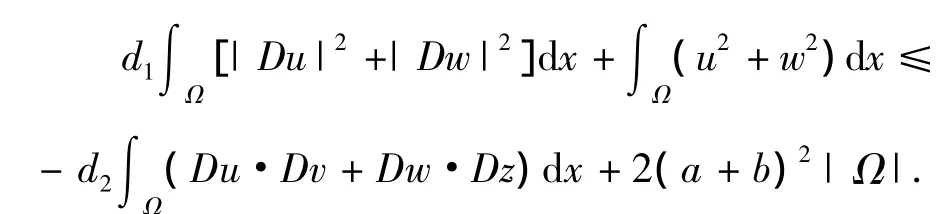
由Holder不等式及(2)，可以得到

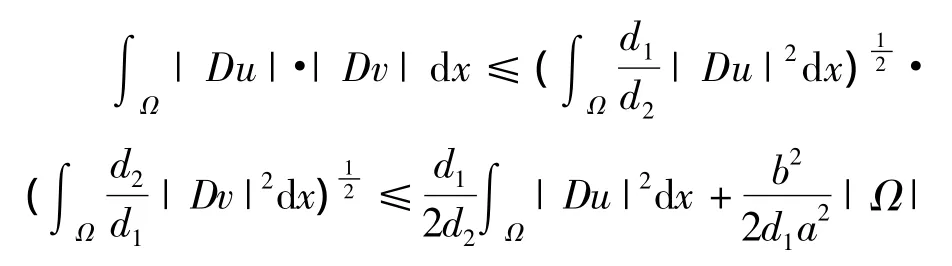
同样地，由Holder不等式及(3)，我们可以得到

所以有

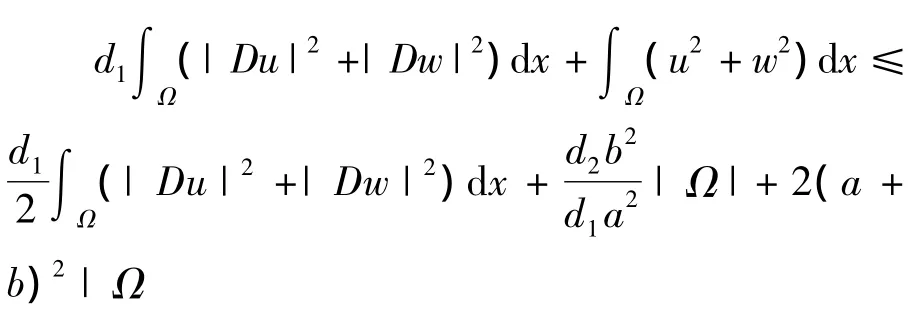
即

因此有

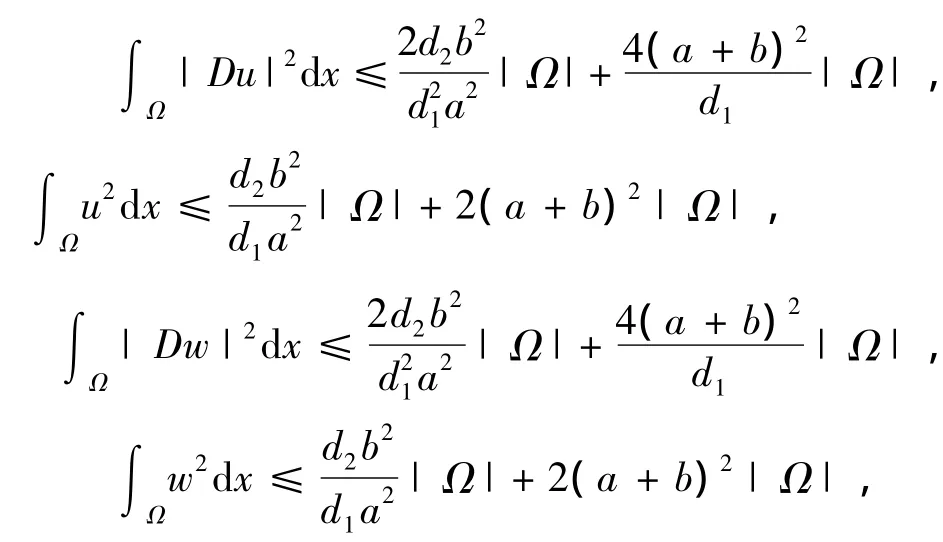
得

所以有

［1］ Marius Ghergu，Vicentiu D.Radulescu.Nonlinear PDEs.Mathematical models in biology，chemistry and population genetics.Springer Monographs in Mathematics.Springer，Heidellberg，2012.

［2］ Zhou J，Mu C L.Pattern formation of a coupled two-cell Brusselator model.J Math Anal Appl，2010，366:679-693.

［3］ Schnakenberg J.Simple chemical reaction systems with limit cycle behaviour.J Theoret Biol，1979，81(3):389-400.