弯曲振动薄圆板的辐射效率

任惠娟，盛美萍

(西北工业大学 航海学院，西安 710072)

辐射效率是描述结构声辐射性能的重要参数，分为“模态辐射效率”和“平均辐射效率”两种，其中“平均辐射效率”反映了结构整体的声辐射情况，又被称为“加权辐射效率”[1]。结构的辐射效率在声辐射研究中具有重要作用，多年来一直为众多学者所关注。

矩形板与圆板是板的两种常见的典型结构形式，矩形板的声辐射效率研究[1－4]相对比较成熟。与矩形板相比，圆板的声辐射效率研究相对滞后并很不完善，其中圆板的模态辐射效率研究主要集中在固定边界、低阶模态及部分频段范围内，如Hansen[5]研究了边界钳定圆板的前几个低阶模态的声辐射效率;Levine[6]研究了高频段内边界钳定轴对称弯曲振动圆板的模态辐射效率;Honda[7]使用典型的薄板理论及改进的薄板理论(Mindlin板理论)研究了边界钳定并嵌在无限大障板上的圆板的模态辐射效率。研究圆板的平均辐射效率较其模态辐射效率更具有现实意义，然而通过文献浏览发现这方面的文献比较少见。

以文献[1]为研究基础，以点激励下弯曲振动的圆板为研究对象，考虑到点激励响应的平均效果，将点激励做了面平均从而获得了薄圆板在固定及简支边界条件下全频段的模态辐射效率，并结合模态叠加理论进一步研究两种边界条件下圆板结构的平均辐射效率，分析平均辐射效率的各种影响因素。本文一方面为改善圆板结构在工程中的减振降噪性能提供理论依据，另一方面也可为与圆板声辐射有关的结构振动研究提供新的思路。

1 薄圆板在点激励下的振动响应

在图1所示的薄圆板置于无限大障板中，圆板上点 C(ρ0，φ0)处受到简谐力 Fejωt的激励，则圆板上任意一点 A(ρ，φ)处的挠度幅值为[8]

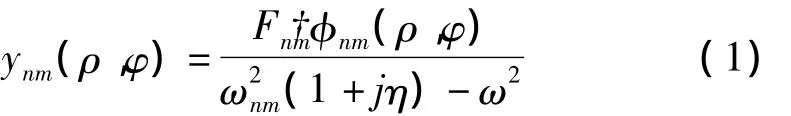
式中:φnm(ρ，φ)为圆板(n，m)阶弯曲振动的振型函数，即φnm(ρ，φ)=Anm[Jm(knmρ)+DnmIm(knmρ)]·cos(mφ)，其中Anm、Dnm与圆板的边界条件有关，且当边界条件为固定及简支时，式中 a为圆板的半径。knm为板中的弯曲波波数，并且，其中ρV为板的体密度，hP为板的厚度，ωnm为圆板第(n，m)阶弯曲振动的圆频率，D为板的弯曲刚度，且，其中E为板的杨氏模量，σ为板的泊松比。η为板的阻尼损耗因子，ω为板的振动角频率。式(1)中表示为:

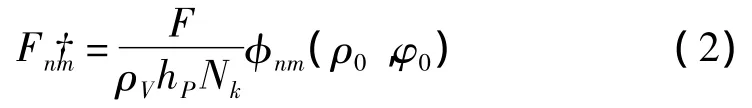
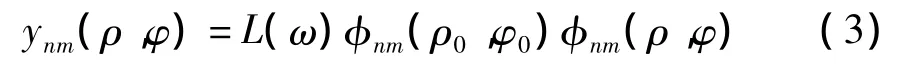
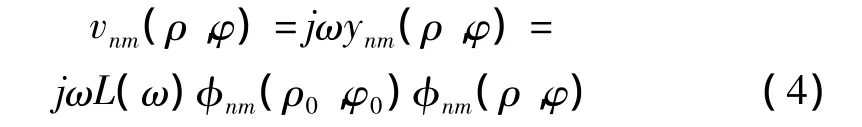
以上各式中的固定及简支边界条件下圆板的特征频率参数knma分别来自于文献[9－10]。

2 薄圆板的模态辐射效率

2.1 圆板的模态声功率及其平均值

将圆板表面分割成无限多的小面元，其中任意两个面元ds及ds'的位置分别用其中心点的极坐标A(ρ，φ)及 B(ρ'，φ')表示，面元 ds'相对于面元 ds的位置用(h，θ)表示，其中h为ds与ds'之间的距离，θ为 h与 ρ之间的夹角，如图1所示。当圆板受到作用于点C(ρ0，φ0)处的简谐力 Fejωt激励并处于第(n，m)阶振动模态时，面元ds的振速幅值如式(4)所示，面元ds'的振速幅值为:

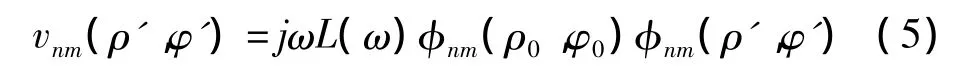
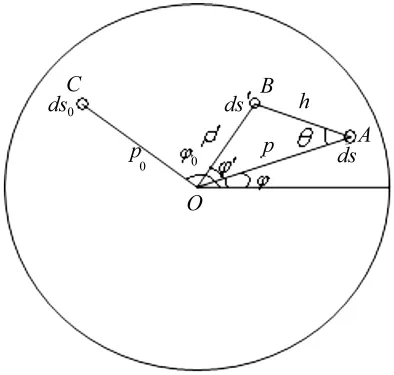
图1 圆板表面示意图Fig.1 Integral sketch in the surface of a circular plate

面元ds'的振动在面元ds处产生的声压幅值为:

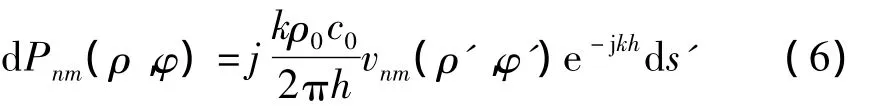
式中:k为声波波数，ρ0为空气的密度，c0为空气的声速。将式(5)代入式(6)并将面元ds'对辐射面进行积分，得到所有面元的振动在面元ds处产生的声压为:

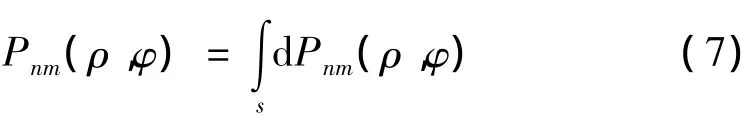
面元ds的声强为:

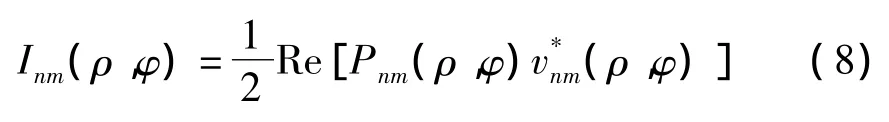
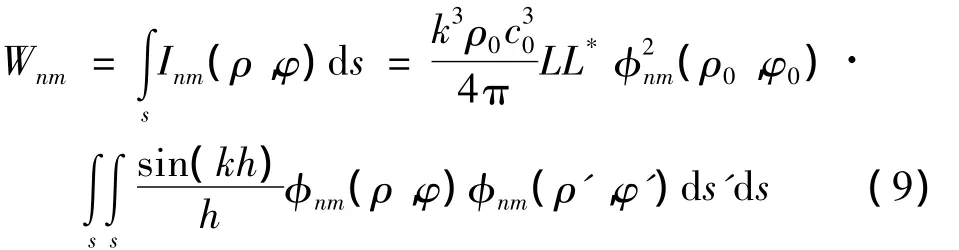
对于点激励情形，通常将激励的作用点位置对板面作平均，以获得响应的平均效果[1]。将上式对激励点进行面平均并将L的表达式代入，得到模态辐射声功率的平均值为:

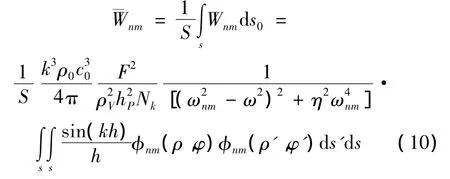
式中:S为圆板的面积。

2.2 圆板的模态均方振速及其平均值

圆板的模态均方振速为

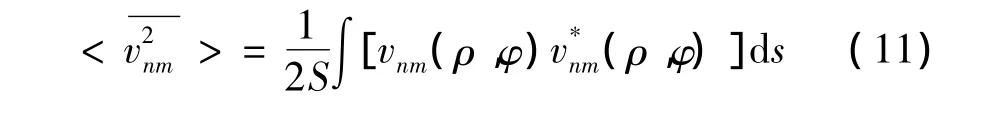
将式(4)代入式(11)得到:

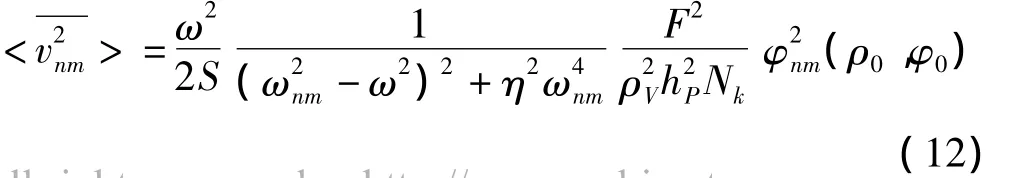
同样，再对上式中的激励点作空间平均，得到模态均方振速的平均值，即:

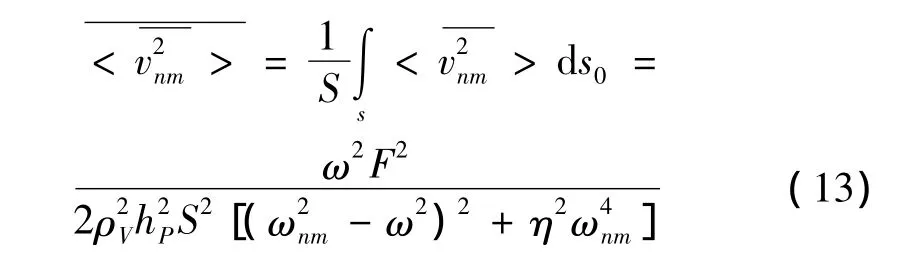
2.3 圆板的模态辐射效率

将式(10)、式(13)代入式(14)后再将该式离散化，并令称为振型函数的形状函数，且 φnm'=[Jm(knmρ)+DnmIm(knmρ)]cos(mφ)，则上式可表示为:

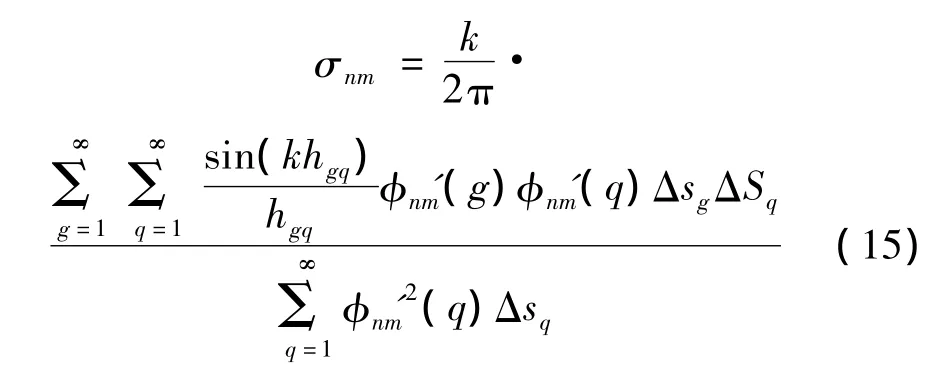
式中:hgq为圆板表面任意两个面元g和q之间的距离，φ'nm(g)和φ'nm(q)分别为面元g和q各自所在处的振型函数的形状函数，Δsg和ΔSq分别为面元g和q各自的面积。

由于面元g和q具有任意性，当二者重合时有hgq=0，但考虑到，因此计算上式的分子时，当g和q重合时，用k代替即可。

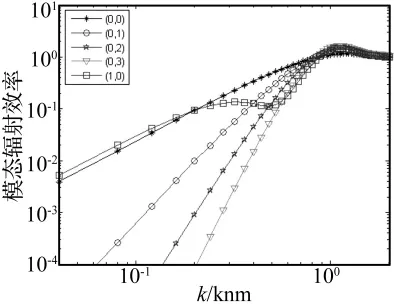
图2 固定边界圆板的模态辐射效率Fig.2 The modal radiation efficiency of a circular plate with clamped boundary

本文通过将声强对圆形辐射面积分获得了圆板的辐射声功率，并对其进行面平均，进而得到了其模态辐射效率。为了说明本文方法的有效性，图2给出了固定边界圆板的几条模态辐射效率曲线，该曲线与文献[7]比较一致性良好，从而证明了本文方法的有效性。

3 薄圆板的平均声辐射效率

3.1 薄圆板的平均声辐射效率

同矩形板的平均辐射效率一样，薄圆板在点激励下作弯曲振动时其平均声辐射效率为:

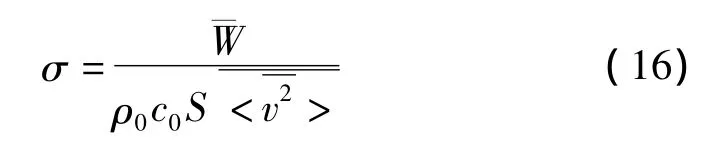
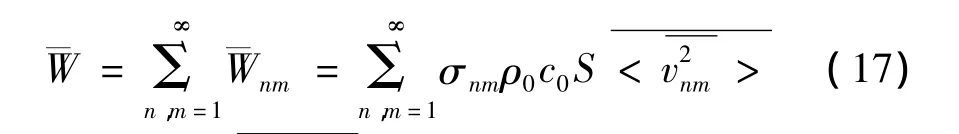
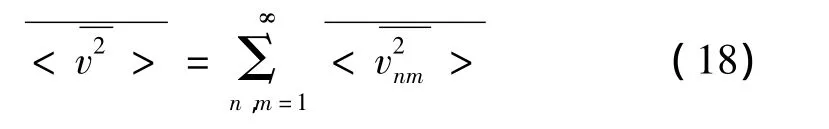
将式(18)、式(19)代入式(17)得到圆板在点激励下的平均辐射效率为:

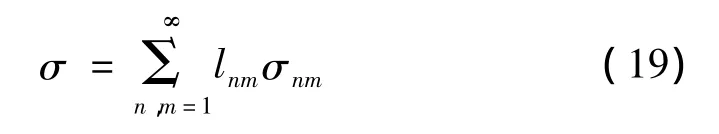
式中，lnm定义为:

炮姜 炮姜为干姜炒到表面微黑、内呈棕黄色，又叫黑姜，无辛散作用，可止血止泻，主要用于虚性出血、寒证腹泻。炮姜还有温经止痛功效。现代研究证明，炮姜水煎剂对应激性胃溃疡、幽门结扎型胃溃疡的发生有显著抑制作用。

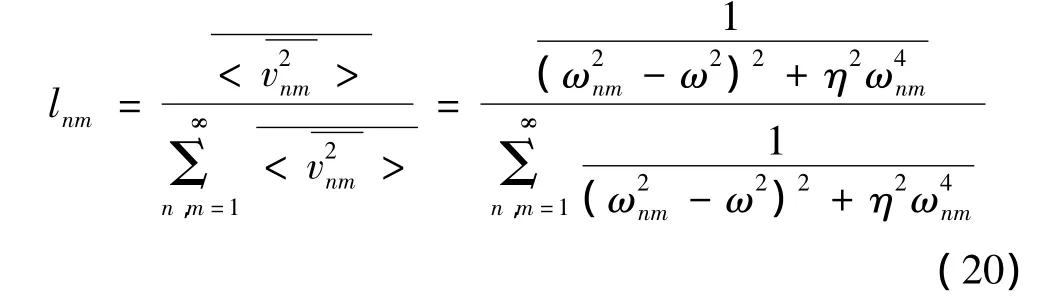
圆板固定及简支边界条件时，在点简谐力激励下，其前100阶的模态辐射效率及平均声辐射效率如图3及图4所示。圆板的参数为:半径0.5 m，厚度3 mm，杨氏模量 2.16 ×1010N/m2，密度7.8 ×103kg/m3，泊松比 0.28，阻尼损耗因子 0.1。

3.2 平均声辐射效率的收敛性分析

平均辐射效率是各阶模态辐射效率的加权平均值，那么参与加权平均的模态个数对平均辐射效率的影响如何呢?图5和图6研究了固定及简支边界圆板参与加权平均的模态个数对其平均辐射效率收敛性的影响情况。可以看出在本文所给的圆板参数下，当参与加权平均的模态个数达到81个(n=0～8，m=0～8)时，两种边界圆板平均辐射效率即开始收敛。

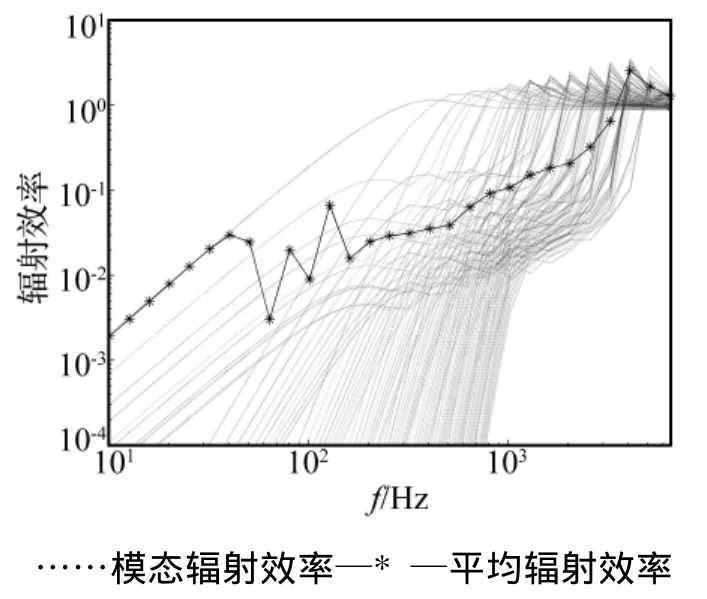
图3 固定边界圆板各阶模态辐射效率及平均辐射效率Fig.3 Radiation efficiency of a circular plate with clamped boundary condition

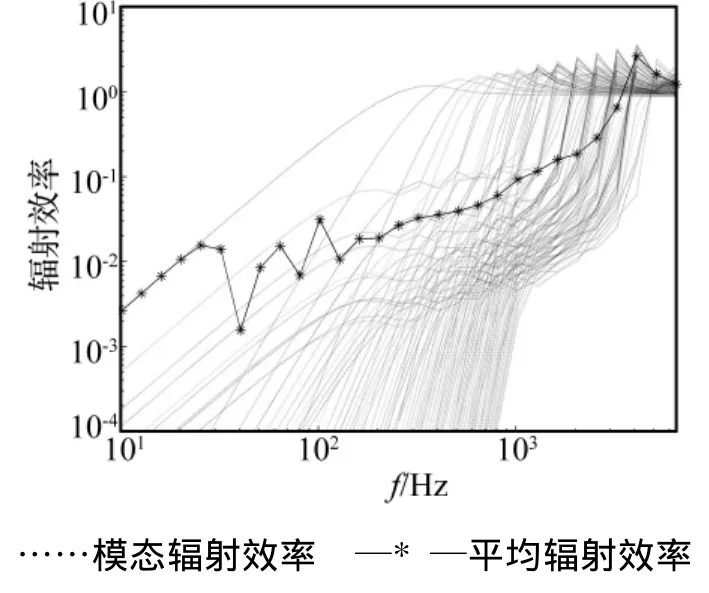
图4 简支边界圆板各阶模态辐射效率及平均辐射效率Fig.4 Radiation efficiency of a circular plate with simply supported boundary condition

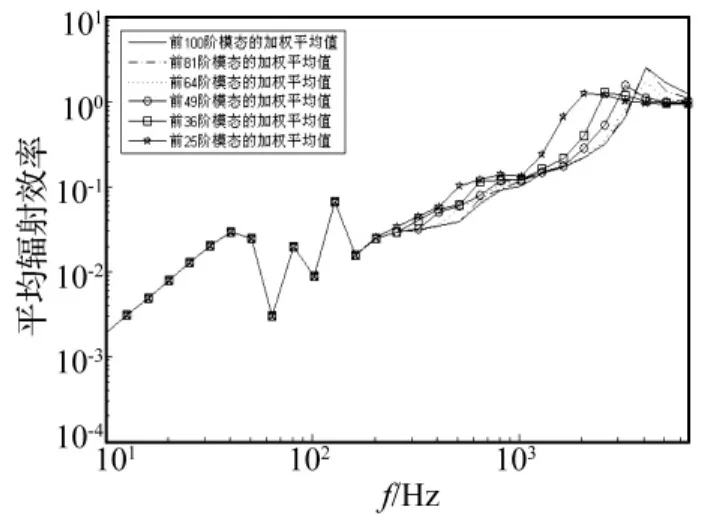
图5 固定边界圆板模态个数对平均辐射效率的影响Fig.5 The influence of the modal quantity to the average radiation efficiency of a circular plate with clamped boundary condition

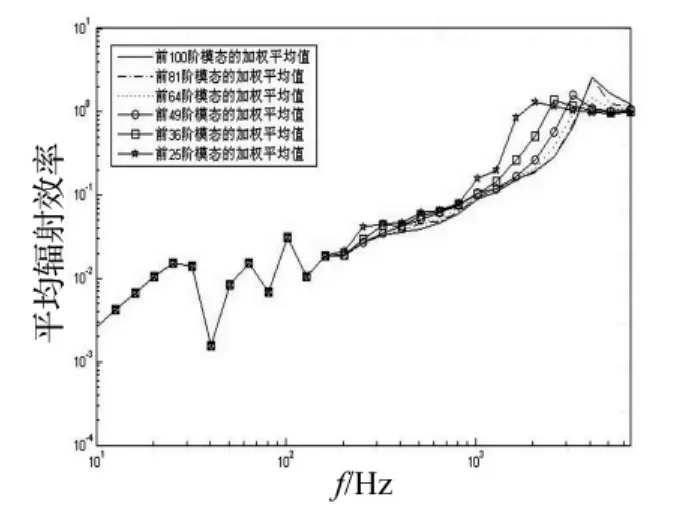
图6 简支边界圆板模态个数对平均辐射效率的影响Fig.6 The influence of the modal quantity to the average radiation efficiency of a circular plate with simply supported boundary condition

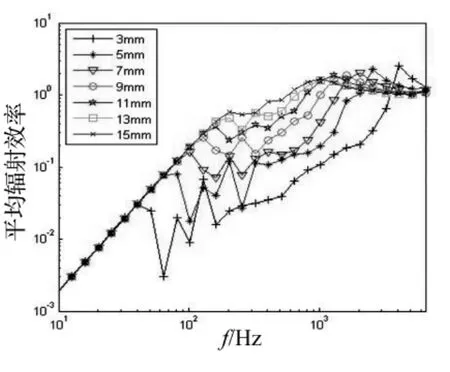
图7 不同厚度的固定边界圆板平均辐射效率对比Fig.7 Comparison of the average radiation efficiency of a circular plate with different thickness

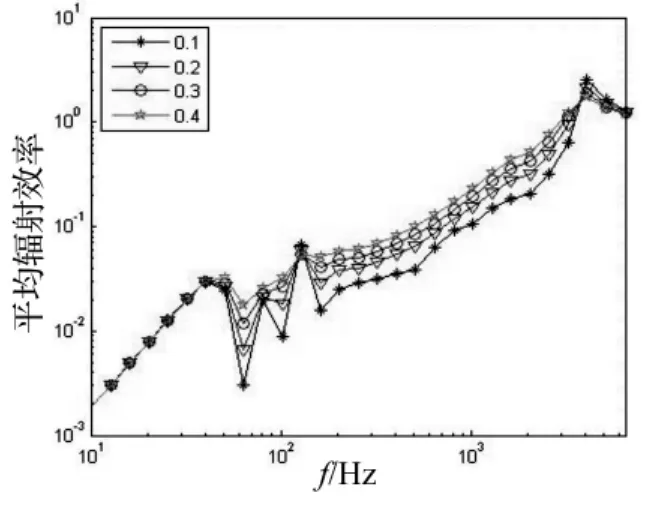
图8 不同阻尼圆板固定边界平均辐射效率对比Fig.8 Comparison of the average radiation efficiency of a circular plate with different damping loss factor

4 圆板参数对平均辐射效率的影响

式(20)表明，当板的材料决定后，圆板结构的平均声辐射效率与激励力的大小及位置无关，而由圆板的厚度、损耗因子、半径、边界条件等四个要素所决定，以固定边界圆板为例，这四个要素对圆板的平均辐射效率的影响分析如下。

4.1 圆板的厚度、阻尼损耗因子及半径对其平均声辐射效率的影响

图7、图8及图9分别给出了固定边界条件下不同厚度(3，5，7，9，11，13，15 mm)、不同损耗因子(0.1，0.2，0.3，0.4)及不同半径(50 m，30 m，10 m)圆板的平均辐射效率对比情况。数值仿真结果说明:在中频段，当频率一定时，圆板的平均辐射效率随着其厚度、阻尼损耗因子的增大及半径的减小而增大。这是由于在中频段随着阻尼因子和厚度的增大以及半径的减小，使得圆板的均方振速平均值减小，从而导致其平均声辐射效率增大[1]。而在低频段平均辐射效率则仅随着圆板半径的增大而增大，并且高频段圆板的平均声辐射效率均趋于1。这是由于在低频段，板的响应主要由最低阶模态的响应决定，其平均声辐射效率近似等于其最低阶模态的辐射效率，而与其他因素无关。在高频段，各阶模态的辐射效率均趋近于1，其加权平均值也将趋近于1，而与其他因素无关。

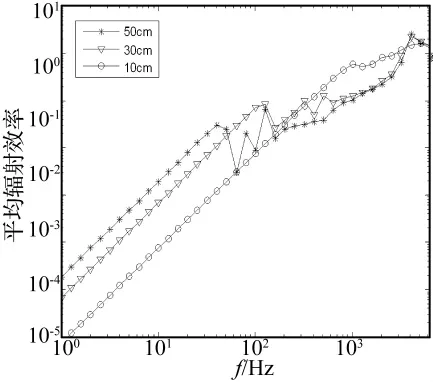
图9 固定边界不同半径圆板平均辐射效率对比Fig.9 Comparison of the average radiation efficiency of a circular plate with different radius

以上结论也适用于简支边界的圆板。

4.2 圆板的边界条件对于其平均声辐射效率的影响

图10给出了固定及简支边界条件下圆板的平均声辐射效率对比情况，结果表明，固定及简支条件下圆板在全频段的平均声辐射效率基本相同。

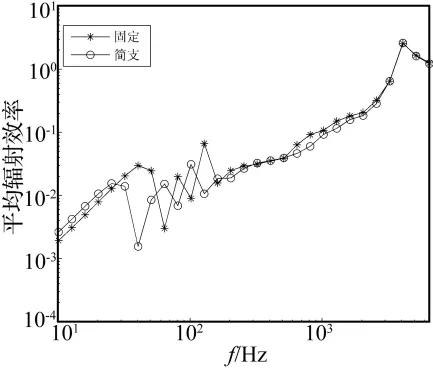
图10 两种边界条件下圆板平均辐射效率对比Fig.10 Comparison of the average radiation efficiency of a circular plate with different boundary condition

5 结论

通过对激励点进行面平均，给出了以上两种边界条件下圆板各阶模态的均方振速及其空间平均值，获得了圆板的各阶模态辐射效率及圆板的平均辐射效率，分析了圆板厚度、阻尼损耗因子、半径及边界条件对其平均辐射效率的影响规律。研究表明:

(1)圆板在点简谐力的激励下，其平均辐射效率与激励力的大小及位置无关，而仅由圆板的厚度、阻尼损耗因子、半径及边界条件所决定。

(2)中、低频段圆板的模态辐射效率及平均声辐射效率随频率的增高而增大，高频段模态辐射效率及平均声辐射效率趋近于1;

(3)当频率一定时，圆板的平均辐射效率在中频段随着其厚度、阻尼损耗因子的增大及半径的减小而增大，而在低频段则仅随着圆板半径的增大而增大;

(4)固定及简支条件下圆板在全频段的平均声辐射效率基本相同。

[1]Xie G，Thompson D J，Jones C J C.The radiation efficiency of baffled plates and strips[J].Journal of Sound and Vibration，2005，280:181－209.

[2]Maidanik G.Response of ribbed panels to reverberant acoustic fields[J].Journal of the Acoustical Society of America，1962(34):809 －826.

[3]Wallace C W.Radiation resistance of a rectangular panel[J].The Journal of the Acoustical Society of America，1972，51(3):946－952.

[4]任惠娟，盛美萍.圆板轴对称弯曲振动的模态声辐射效率，噪声与振动控制[J].2011，31(4):51－54.

[5]Hansen C H，Bies D A.Optical holography for the study of sound radiation from vibration surfaces[J].Journal of the Acoustical Society of America，1976，60:543－555.

[6]Levine H.A note on the acoustic power output of a circular plate[J].Journal of Sound of Vibration，1988，121(2):269－275.

[7]Honda Y，Matsuhisa H，Sato S.Radiation efficiency of a baffled circular plate in flexural vibration[J].Journal of Sound and Vibration，1983，88(4):437－446.

[8]Soedel W.Vibrations of shells and plates[M].New York，Marcel Dekker，1993.

[9]Leissa A W，Narita Y.Journal of sound and vibration[J].Natural Frequencies of Simply Supported Circular Plates，1980，70:221－229.

[10]Airey J R.Proceedings of the physical society(London)[J].The Vibration of Circular Plates and Their Relation to Bessel Functions，1911，23:225 －232.

[11]Cremer L，Heckl M，Ungar E E.Structure-borne Sound(2nd)[M].Edition Springer Berlin，1988.