直线滚动导轨副动态特性分析
李 磊,张建润,刘洪伟
(1.东南大学 机械工程学院,南京 211189;2.江苏科技大学 机械工程学院,江苏 镇江 212000)
直线滚动导轨副由于运动阻力小、定位精度高等优点逐渐取代滑动导轨成为高速高精度数控机床的重要功能部件,其动态特性建模特别是导轨滑块结合面建模精度对机床整机动态分析有重大影响。国外早在上世纪90年代便开始对滚动导轨副动态特性进行了深入研究,主要包括结合面运动机理研究和动态特性建模研究[1-2]。近年来,结合面非线性特性引起了国外学者的重视[3]。国内对于直线滚动导轨建模研究也广泛开展:刘阳等[4]通过有限元方式建立了导轨结合面模型应用于机床整机建模和分析并进行了实验验证,毛宽民等[5]结合有限元方法提出了一种新的直线滚动导轨副结合部动力学模型,文献[6]使用弹簧阻尼单元模拟滑块导轨结合面取得了良好的结果。以上模型主要是基于有限元方法,其建模精度受到结合面单元分布形式和结合面参数的影响;同时,由于忽略了结合面非线性因素的影响,建模精度不高,制约了高速、高精度数控机床动态特性建模和分析的可靠性。
基于前人的研究[1-2,7],本文针对一款直线滚动导轨,探讨结合部刚度计算方法,通过模态理论和拉格朗日方程建立该导轨副动力学模型,分析其固有特性,并运用模态实验进行了分析验证;同时,考虑结合面非线性特性,基于实验讨论了预紧力和外部激励等对导轨系统刚度和阻尼特性的影响,为精确建立高速、高精度机床整机动态模型和系统稳定性分析奠定了基础。
1 导轨系统结合面模型及其特性参数获取
直线滚动导轨主要由导轨、滑块、保持架以及导轨滑块间的滚动钢球组成(如图1),其动态特性很大程度上取决于钢球和导轨滑块间的结合部刚度。为此,建立导轨系统动态特性模型首先要建立结合部刚度模型,方法主要有赫兹理论法和基于模态理论的模态参数法。
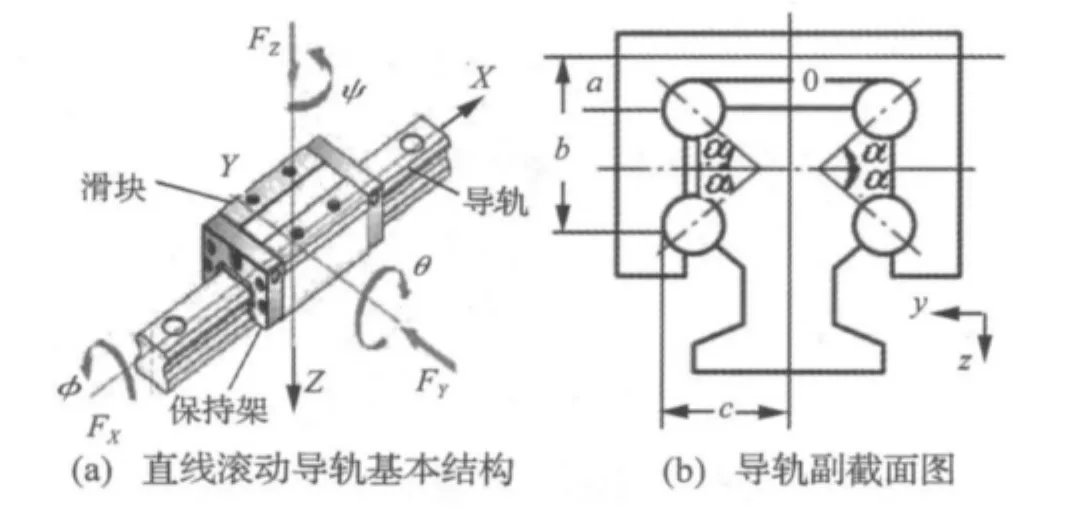
图1 直线滚动导轨副结构简图Fig.1 Configuration of linear motion guide(LMG)
1.1 赫兹理论法
赫兹理论是接触力学的经典理论,由赫兹理论可知滚动导轨副的钢球-导轨及钢球-滑块结合面接触区域是椭圆面。为了计算局部变形,可以这样简化:每个物体可以看成是弹性半空间体,载荷作用在平表面的一个小的椭圆区域内。根据赫兹理论,钢球刚度可由下式获取[2]:

1.2 模态参数识别法
滚动导轨副工作时承受的载荷可以分解到垂直于滑块连接面(法向)和侧向(切向)。对机床导轨的每个方向进行刚度测试时,导
轨可以简化成一个单自由度系统。导轨与滑块接触面的每个方向的接触刚度及其相应的阻尼都可通过识别滑块在导轨上所表现出来的模态来获得[6]。
根据分量分析法,通过实验测得导轨副传递函数(图2),通过半功率法可以识别该方向上的刚度及阻尼值:
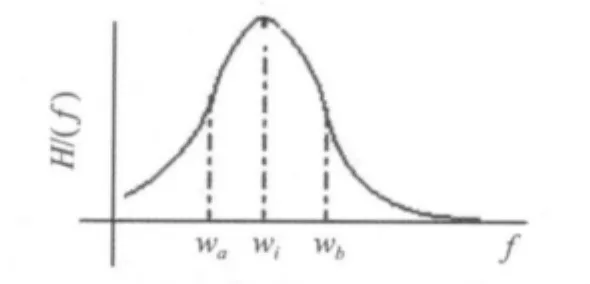
图2 直线滚动导轨传递函数Fig.2 Transfer function of linear motion guide

其中:ζr=(ωa- ωb)/2ωi为阻尼比,M 为滑块质量,f=ωi为系统频率,ωa、ωb为半功率点。
赫兹理论法可获取系统静刚度,模态参数识别法获取系统动刚度,文献[6]中证明了两种方法的在滚动导轨结合面建模中的一致性和可靠性。
2 直线滚动导轨系统动力学特性理论分析[1]
拉格朗日方程利用广义坐标描述非自由质点系的运动,在解决微幅振动问题和刚体动力学问题中起了重要的作用:

滚动直线导轨的系统动能可由下式求解:

由于导轨滑块结合面表现出弹性阻尼特性,可以将滚珠简化成弹簧,其势能为:

其中:k=KV/4lsin2α[1],为钢球导轨面的单位长度法向刚度,KV为铅垂方向的刚度(根据模态参数法获取),α为滚珠与滑块的接触角,l为接触区长度,x为变形量,其它结构见图1。
将系统动能与系统势能代入拉格朗日方程,运用MATLAB软件开发通用计算程序求解得到[1]:
滑块振动的竖向固有频率:
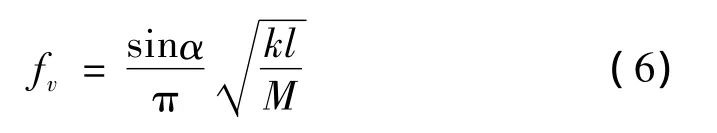
滑块振动的摆动固有频率:
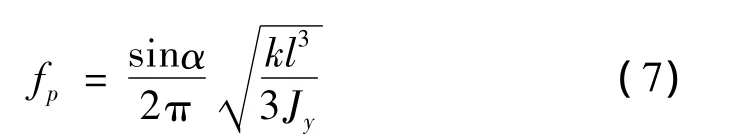
滑块振动的斜向振动频率:
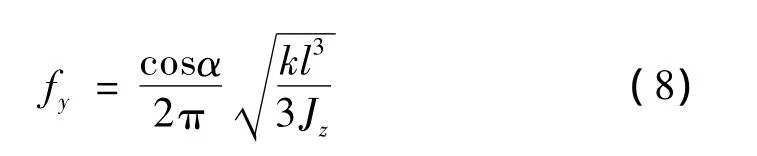
由f=ω/2π可得低阶和高阶滚动固有频率。且:

以上固有频率表达式表明:系统固有频率是结合面刚度的函数(不考虑阻尼)。然而,结合面特性影响因素众多且表现出强烈的非线性,要建立准确的机床分析模型必须考虑导轨结合面的非线性特性。有学者提出结合面刚度和阻尼的表达式[8]:
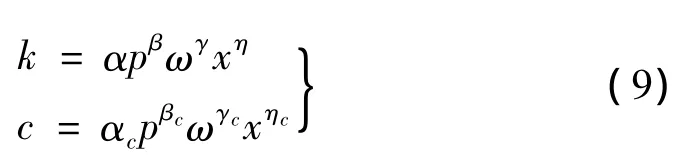
其中:p,ω,x分别为法向压力、外载荷激振频率和单位结合面位移激励幅值;α,β,γ,η为特性系数,其值与结合面材料加工方式、表面粗糙度润滑状态和油膜介质类型相关。后面将进一步对其非线性特性进行讨论。
3 实验分析
结合一款滚动直线导轨分析其动态特性,其具体参数如表1(滑块质量为4.7 kg,刚度通过模态实验法获取):

表1 导轨参数Tab.1 Parameters of linear motion guide
将导轨参数代入可求出导轨滑块系统的前五阶固有频率(见表2)。
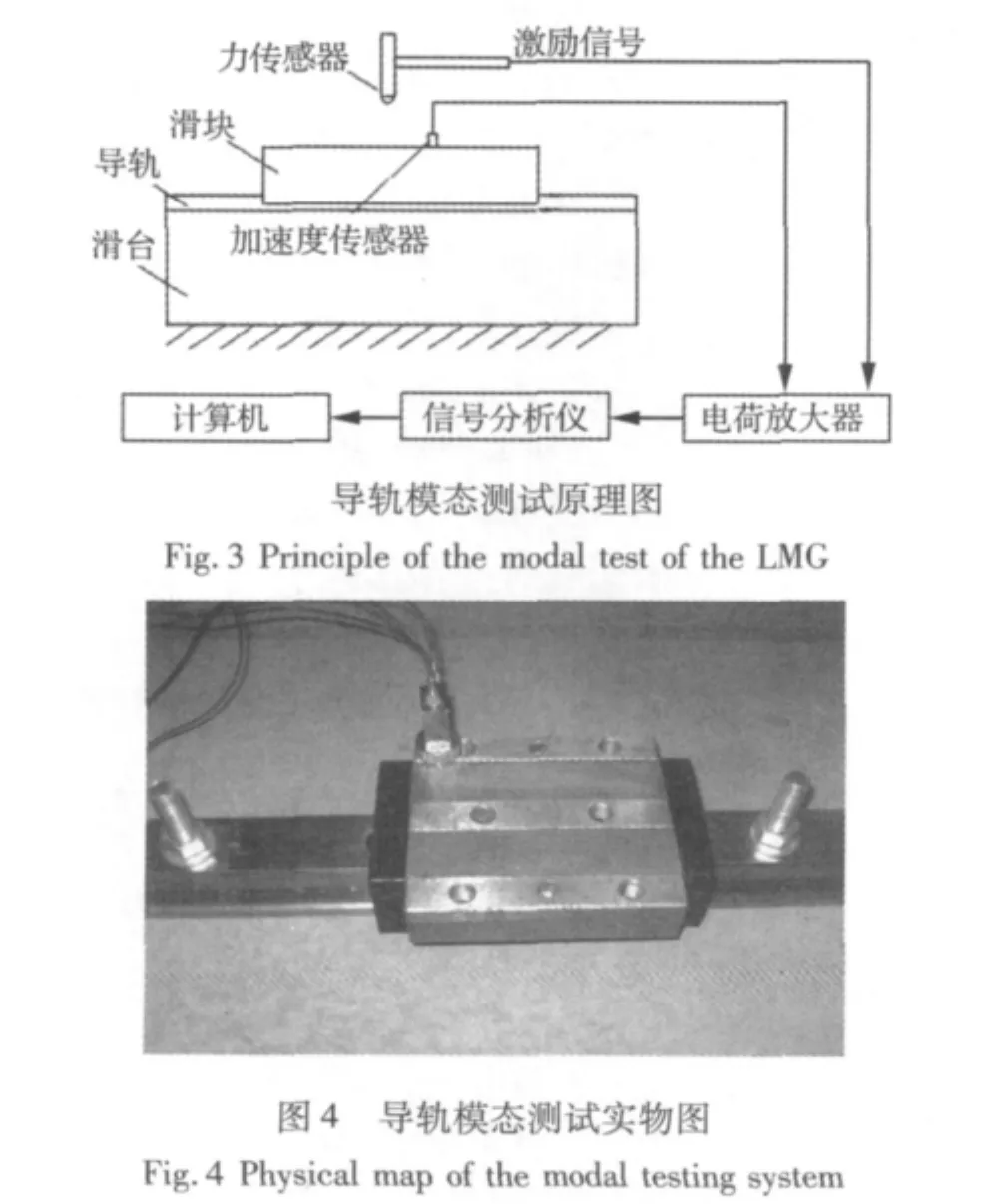
对该导轨用大直径螺栓固定于地面进行约束状态下的模态实验,实验原理如图3所示,实物图如图4所示,采用力锤对滑块进行激励,使用三向加速度传感器获取加速度信息,通过频谱分析并结合振型分析得到其传递函数如图5所示。
根据模态实验结果(表2)可以看出,理论值跟实验值基本吻合,最大误差在5%左右。然而,该模型其没有考虑阻尼特性且忽略了结合面非线性,仅能对系统动态特性进行初步计算。对于高档机床而言,结合面非线性对系统动态特性和加工稳定性有重要影响,下面将重点予以讨论。
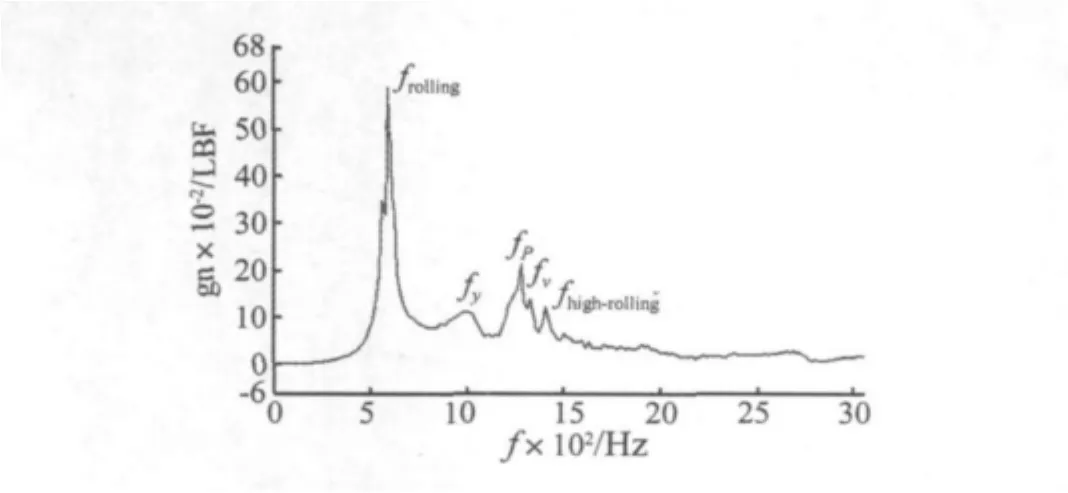
图5 导轨系统模态频率曲线Fig.5 Frequent curve of the linear motion guide

表2 实验结果与理论值得比较Tab.2 Comparing of the result of theory and testing
4 导轨系统非线性特性分析
由于结合面作用机理还不明确,在理论上获得式(9)的准确表达是非常困难的。为此,仅对导轨结合面非线性特性进行定性分析。
4.1 预紧力对系统动态特性的影响分析
滚动导轨预紧一般通过调节钢球直径实现,调节预紧力可以提高导轨系统初始接触力从而提高其刚性和定位精度。由前面推导过程可知,滚动导轨固有频率和结合面刚度直接相关,适当提高预紧力大小可以改善滚动导轨副的动态特性,随着预紧力的提高系统各阶固有频率有了显著提高(如图6所示)。文献[9]从分析系统响应角度指出:提高滚动导轨预紧力可以提高系统刚度,进而改善机床动态性能。但是,当钢球直径过大带来结合面摩擦力的提高,破坏了结合面微观连接机制,导致能量损耗,系统动态特性出现无规律的变化。为此,有必要根据机床动态特性要求及加工参数合理的选择导轨副预紧力的大小。
4.2 外部激励对系统动态特性的影响分析
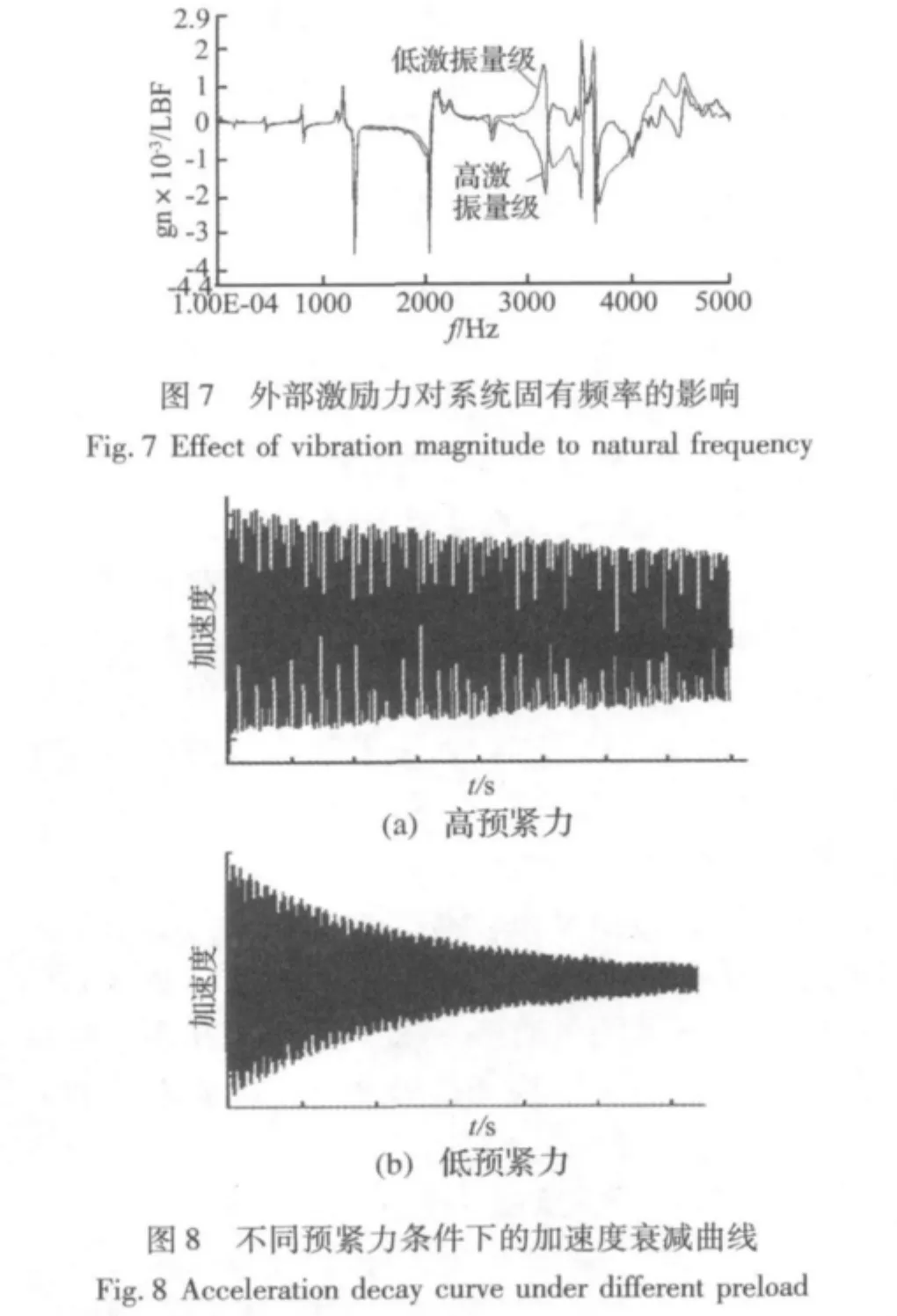
为了研究外部激励对系统动态特性的影响,对自由状态下的导轨滑块系统做模态实验,在相同预紧力条件下,改变外部激励的幅值,实验结果如图7所示。
测试结果显示:随着振动量级的增大,自由状态下系统的低阶固有频率没有发生明显变化,而高阶固有频率(3 000 Hz以上)发生了有规律的衰减,该结果和文献[10]基本一致。这主要是由于导轨-滑块系统在一定的预紧力条件下能够保持一定的刚度特性,使得系统动态特性维持稳定状态,但随着外载荷的提高,较大的外载荷导致系统刚度下降并表现出明显的阻尼特性,导致了系统固有频率的衰减。为此,低阶状态下可以将该系统近似为线性系统,而对于高速高精度及重载数控机床,高阶动态特性不能忽略,必须考虑结合面非线性对机床动态性能的影响。

图6 预紧力对系统固有频率的影响Fig.6 Effect of preload to natural frequency
4.3 结合面阻尼特性分析
一般认为阻尼是影响机械系统稳定性的重要因素,而结合面是引起结构阻尼的主要原因。根据接触理论,假设结合面是无数峰-谷组成的不平面,微运动意味着在不产生宏观运动条件下,其峰-峰,峰-谷之间出现相对非常小的局部接触和运动。伴随微运动,系统动载荷会逐渐耗散,微运动区域会随接触载荷的降低而减小,幅度会随载荷幅值的增加而增加。当微运动现象逐渐转变为宏观滑动,从而导致结合面的阻尼或能量耗散增加。
图8为不同预紧下,结构加速度随时间衰减的曲线,可以明显看出,低预紧力结构的加速度衰减率大大高于高预紧力(或整体结构)情况,而加速度的衰减正是由于结合面阻尼引起的能量损耗进而影响系统稳定性。因此,考虑预紧力对系统稳定性影响是机械系统动力学设计的重要方面。
5 结论
(1)分析了滚动直线导轨刚度的计算方法,结合拉格朗日方程建立某导轨系统动态特性方程,通过MATLAB开发了通用计算程序;模态实验结果和理论值误差在5%左右,表明该方法可以应用于滚动直线导轨动态特性的初步分析;
(2)实验表明:由于结合面的存在,直线滚动导轨表现出强烈的非线性动态特性,其刚度值、阻尼值和固有频率是法向压力(预紧力)和外载荷激振量级的函数,在低频段可以近似为线性系统,但在高频段应当考虑非线性对系统动态性能的影响;
(3)仅讨论了预紧力和外部激励对导轨结合面的作用,其结合部运动机理及阻尼特性还有待于进一步的理论研究和大量的实验验证,从而为提高机床整机动态特性分析精度和机床加工稳定性提供理论和实验依据。
[1] Ohta H.Vibration of linear guideway type recirculating linear ball bearings[J].Journal of Sound and Vibration,2000,235(5):847-861.
[2] Yi Y S,Kim Y Y,Choi J S,et al.Dynamic analysis of a linear motion guide having rolling elements for precision positioning devices[J].Journal of Mechanical Science and Technology,2008,22(1):50-60.
[3] AI-Bender F,SymensW.Characterization offrictional hysteresis in ball bearing guideways[J].Wear,2005,258(11-12):1630-1642.
[4] 刘 阳,李景奎,朱春霞,等.直线滚动导轨结合面参数对数控机床动态特性的影响[J].东北大学学报(自然科学版),2006,27(12):1369-1372.LIU Yong,LI Jing-kui,ZHU Chun-xia,et al.Influence of linear rolling guide joint on dynamic behavior of NC machine tools[J].Journal of Northeastern University 2006,27(12):1369-1372.
[5] 毛宽民,李 斌,谢 波,等.滚动直线导轨副可动结合部动力学建模[J].华中科技大学学报,2008,36(8):85-88.MAO Kuan-min,LI Bin,XIE Bo,et al.Dynamic modeling of the movable joint on rolling linear guide[J].Journal of Huazhong University of Science & Technology,2008,36(8):85-88.
[6] 李 磊,张胜文,于 洋,等.滚动导轨结合面参数识别及仿真分析[J].江苏科技大学学报,2009,23(2):142-145.LI Lei,ZHANG Sheng-wen,YU Yang,et al.Parameter identification and simulation analysis of the rolling guideway[J].Journal of Jiangsu University of Science and Technology ,2009,23(2):142-145.
[7] 周传宏,孙健利,杨叔子.滚动直线导轨副的振动模型研究[J].机械设计,1999(2):21-24.ZHOU Chuan-hong,SUN Jian-li,YANG Shu-zi.A study on the vibration model of rolling linear guiding pairs[J].Jixie Sheji,1999,(2):21-24.
[8] 张广鹏,史文浩,黄玉美.机床导轨结合部的动态特性解析方法及其应用[J].机械工程学报,2002,38(10):114-117.ZHANGGuang-peng, SHIWen-hao, HUANGYu-mei.Analysis method of dynamic behaviors of guideway joint and its application in machine tools design[J].Chinese Journal of Mechanical Engineering,2002,38(10):114-117.
[9] Lin C Y,Hung J P,Lo T L.Effect of preload of linear guides on dynamic characteristics of a vertical column–spindle system [J].International Journal of Machine Tools &Manufacture,2010,50(8):741-746.
[10] 陈学前,杜 强,冯加权.螺栓连接非线性振动特性研究[J].振动与冲击,2009,28(7):196-198.CHEN Xue-qian,DU Qiang,FENG Jia-quan.Nonlinear vibrational characteristic ofbolt-joints[J].Journalof Vibration and Shock ,2009,28(7):196-198.

