基础不均匀沉陷诱发车-桥耦合动力学建模与分析
朱怀亮, 方英东, 谢 严, 王 雪
(1.上海大学 力学系,上海 200444;2.上海市应用数学和力学研究所,上海 200072)
对于软土性地基上的高速轨道系统来说,基础下沉是一个普遍性的问题。由基础不均匀沉陷所造成的局部沉降差直接导致了轨道的不平顺,诱发车-桥系统振动加剧,严重影响乘车的舒适度和行车的安全性。因此,随着高速、重载、大跨度车-桥运输系统的建设,探讨基础不均匀沉陷对车-桥系统动力响应和特性的影响已越来越引起相关研究者的高度关注[1-3]。
为了揭示基础不均匀沉陷导致的局部沉降差对车桥耦合振动的影响,本文研究轴向力作用下连续梁桥模型当某个支座发生沉陷而诱发的轨道不平顺问题,提出了描述支座沉陷激励的力学模型,建立基础局部沉陷和桥梁轴向力作用下的车-桥系统耦合动力学方程,数值模拟并分析了基础沉陷、行车速度、轴向力和结构动力参数等对系统动力响应和特性的影响。
1 车-桥系统力学模型
车-桥系统的力学模型如图1所示。其中车辆采用二分之一车模型,桥梁为具有弹性约束的连续梁,分别建立车辆和桥梁的动力学方程[4-7]。

图1 车辆-桥梁基础系统Fig.1 Vehicle-bridge system
1.1 车辆振动微分方程
在图示坐标系下,就表示车辆的两系弹簧-阻尼-质量系统由达朗贝尔原理建立振动控制方程,其中车体可考虑沉浮(竖向)运动和点头(旋转)运动,构架和轮对则只考虑沉浮(竖向)运动。
1.1.1 车体沉浮运动
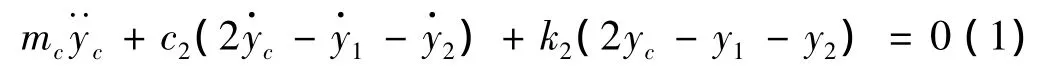
1.1.2 车体点头运动

1.1.3 左转向架沉浮运动

1.1.4 右转向架沉浮运动

式中:mc为车体质量;m1和m2分别为左、右构架与轮对质量之和;yc为车体质心的竖向位移(沉浮);θc为车体转角(点头);y1和y2分别为左右转向架质心的竖向位移;Ic为车体的点头刚度;k1为一系垂向刚度;c1为一系垂向阻尼系数;k2为二系垂向刚度;c2为二系垂向阻尼系数。a为车辆两轮之间的距离,yb(x,t)为桥梁的竖向位移。
1.2 桥梁振动微分方程
将桥梁模拟为由多个线性、对称弹性支承和阻尼器作用下的连续梁,设单位长度质量为mb,长度为l,抗弯刚度为EbIb。不考虑剪切变形和转动惯量的影响,车辆对桥梁的作用力为:

式中:p1(x,t)、p2(x,t)分别为左、右车轮与桥梁间的耦合作用力,η1、η2分别为两轮处由桥面和轨道不平顺引起的时变激扰函数,δj为狄里克雷函数,具体为:

式中:ν为行车速度,于是,桥梁振动微分方程表示为:

式中:Nb为桥梁的轴向力,表示了桥梁和轨道中因基础沉陷、结构变形、多余约束和温度改变等引起的纵向作用力。对于连续梁,应用振型分解方法[8-9],将yb(x,t)代入式(8),沿梁长积分并联立式(1)~式(4)和式(8),得到车-桥耦合系统的动力学控制方程为:

式中:{q}为广义位移向量,{q}=[yc,θc,y1,y2,q1,q2,…,qn]T;[M]为广义质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;{P}为广义力向量。
2 基础沉陷模型
当支承发生下沉时,会导致桥梁局部坍陷或形成沉降三角坑,从而引起轨道严重的几何不平顺,如图2(a)所示,其中下沉量为Ω。一般情形下,轨道几何不平顺可以用某个简谐波近似描述为:

图2 桥梁支承沉陷引起的三角坑和轨道不平顺Fig.2 Rail irregularity with local subsidence of foundation
如图2(b),其中λi为不平顺波长,ei为波深。对图2(a)所示的桥梁沉降三角坑,利用傅里叶级数展开。设l1=l2=l/2,在图示坐标系下桥梁的沉陷方程为:
左半段:

右半段:

在其定义域内进行偶延拓,并将其表示成一系列的谐波激扰函数,其中各系数分别为:

将式(10)、式(11)代入式(12)得:

整理得:

不平顺激扰函数表示为:
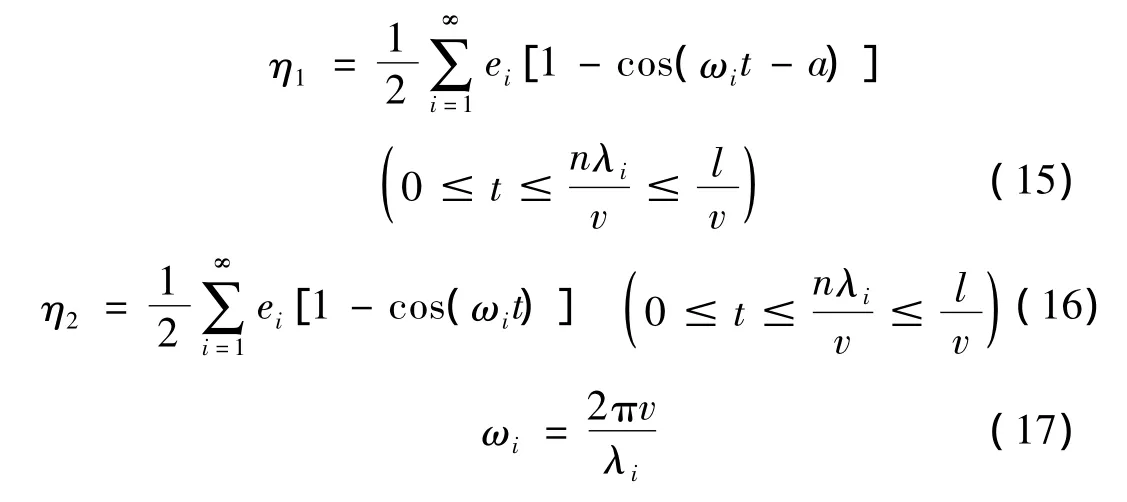
3 算例分析
3.1 参数选择
对于图示车-桥耦合系统,采用Newmark-β法迭代求解系统的动力响应,不平顺函数取6阶傅里叶级数即可获得稳定的激励效果[10-11]。文献[12]反映了不同基础沉陷、桥梁轴向力、车辆刚度和阻尼等系统特性对动力响应的影响和变化规律,其中车辆参数为:车体质量 mc=3.85×104kg,前、后转向架与车轮的质量和均为 m1=m2=4.33 ×103kg,转动惯量 Ic=2.446 ×106kg·m2,车辆前后轮间的距离均为a=8.4 m,刚度系数 k1=k2=2.535×106N/m,阻尼系数 c1=c2=1.920 8×106N·s/m,车辆速度分别取v=20 m/s、40 m/s和60 m/s。桥梁参数为:取双跨连续梁,跨度l=100 m,单位梁长质量mb=1.08×104kg/m,抗弯刚度 EbIb=5.18×1010N·m2,cd=3.21×105N·s/m,kd=2.535×106N/m。桥梁的轴向预拉力 Nb=5×107N。
3.2 算例分析
3.2.1 基础沉陷对系统耦合振动的影响
图3~图6分别表示了桥梁和车辆各动力响应与基础沉陷量之间的关系,可以看出基础局部沉陷对车-桥系统振动位移和加速度的影响。无论对车体和桥梁来说,随着支承沉陷量的增加,其动态响应的各幅值都明显增大,由系统的振动加速度变化曲线还可表明,过大的局部沉陷量伴随着明显的动力冲击,这不仅直接关系到车辆运行的舒适度和安全性,而且还会严重影响桥梁的使用寿命。
3.2.2 车速对耦合振动的影响
图7~图10分别表示了速度对车-桥系统动力响应的影响,可以看出行车速度显著改变了系统的振动形态。在一定条件下,随着车辆速度的增加,桥梁和车体的振动响应以及车桥之间相互作用力的幅值都随之增大,同时使得振荡加剧、高阶模态振动被激发,特别是当车辆高速通过发生基础局部沉陷的桥梁时,车-桥之间的动反力显著增大,同样伴随着明显的振动冲击。


3.2.3 轴向力对耦合振动的影响
图11和图12分别给出了支承沉陷条件下不同轴向力作用所引起的车-桥动力响应,比较可以看出,当基础发生一定沉陷时(下沉量Ω=0.05 m),不同的轴向力作用会对系统的动力响应产生不同程度的影响。一般说来,随着桥梁的轴向拉力加大,桥梁中点的振动位移和车体重心处的振动位移幅值都会相应减小,施加合理的轴向力能在一定程度上控制因支承沉陷而引起的振动响应。
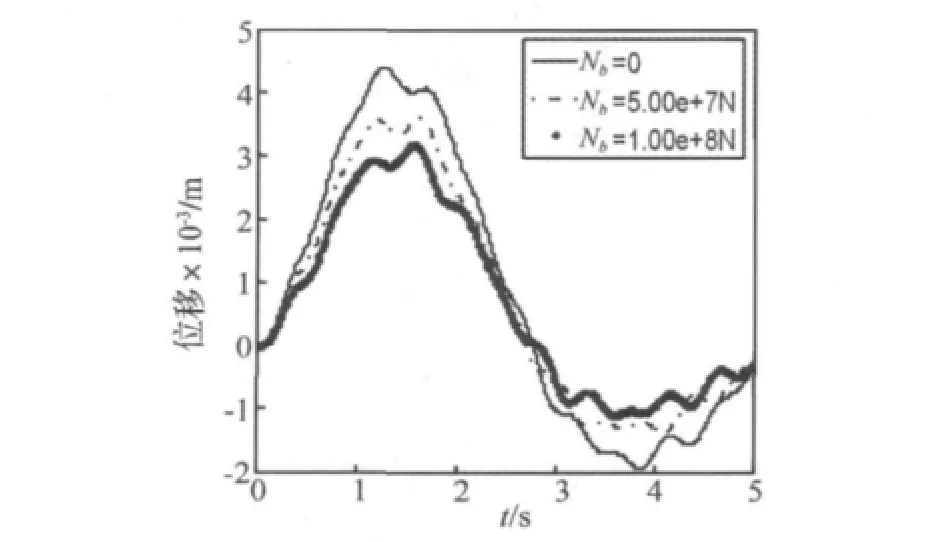
图12 桥梁第一跨中点竖向位移Fig.12 Displacement at midpoint of first span
4 结论
(1)桥梁基础的不均匀沉陷会对车-桥耦合系统的动力响应产生明显的不利影响。一般说来,沉陷量越大,系统各响应的振动幅值也越大,过大的局部沉陷量还伴随着明显的动力冲击。因此控制桥梁基础的不均匀沉陷,特别是在沿海软土地区,对减小车-桥耦合系统的振动响应、提高车辆运行的平顺性和安全性具有积极而重要的意义。
(2)系统的动态响应会随着车速的提高而明显加大,特别是当车辆高速通过桥梁时,会引起结构较大幅值的横向振动,车-桥间的动反力也急剧增大,并对车辆和桥梁造成较大的冲击。
(3)在考虑基础不均匀沉陷的情况下,桥梁轴向力会对系统动力学响应产生明显的影响。随着轴向拉力的加大,桥梁和车体的振动响应都会不同程度地减小,特别是对于大跨度和轻柔型桥梁系统来说,轴向力和轴向约束对系统横向振动的影响也是不可忽略的因素。
[1] 高建敏,翟婉明.车辆-轨道耦合动力学在轨道下沉研究中的应用[J].西南交通大学学报,2007,42(4):431-435.
[2] 韩义涛,姚 力.基础沉降对土路上板式轨道动力性能影响分析[J].铁道工程学报,2007(10):28-31.
[3] 王学军.基础沉降对加宽桥梁上部构造的影响分析[J].中国港湾建设,2006(6):11-13.
[4] 肖新标,沈火明.3种车桥耦合振动分析模型的比较研究[J].西南交通大学学报,2004,39(2):1-4.
[5] Ju S H,Lin H T.A finite model of vehicle-bridge interavtion considering braking and acceleration[J].Journal of Sound and Vibration,2007,303:46-57.
[6] 丁南宏,钱永久,林丽霞,等.双链式悬索桥在单车荷载下的振动特征[J].振动与冲击,2010,29(7):216-220.
[7] 林 海,肖盛燮,桥梁车辆振动分析理论评述[J].重庆交通学院学报,1998,17(3):1-9.
[8] Zheng D Y,Cheung Y K,Au F T K,et al.Vibration of multi-span non-uniform beams under moving loads by using modified beam vibration functions[J].Journal of Sound and Vibration[J].1998,212(3):455-467.
[9] 沈火明,肖新标.插值振型函数法求解移动荷载作用下等截面连续梁的动态响应[J].振动与冲击,2005,24(3):27-30.
[10] Michaltsos G,Sophianopoulos D K,Ounadis A N.The effect of a moving mass and other parameters on the dynamic response of a simply supported beam[J].Journal of Sound and Vibration,1996,191(3):357-362.
[11] 崔圣爱,祝 兵,白峰涛,等.琼州海峡跨海斜拉桥方案车桥系统耦合振动仿真分析[J].振动与冲击,2011,30(5):106-110.
[12] 朱怀亮,谢 严,胡开封,等.考虑轴向力作用下车-桥耦合系统的动力学建模与分析[J].南昌大学学报(工科版),2008,30(4):389-393.
[13] Cai C W,Cheung Y K,Chan H C.Dynamic response of infinite continuous beams subjected to a moving force-an exact method[J].Journal of Sound and Vibration,1998,123(3):461-472.
[14] 刘 富,练松良.轨道纵向刚度变化对快速列车轮轨受力的影响[J].同济大学学报,2001,29(11):1276-1281.

