坠落式危岩崩落的激振效应与求解

唐红梅，王 智，陈洪凯，鲜学福

(1.重庆交通大学 岩土工程研究所，重庆 400074;2.重庆大学 西南资源开发及环境灾害控制工程教育部重点实验室，重庆 400040)

危岩是指由多组岩体结构面切割并位于陡崖或陡坡上稳定性较差的岩石块体及其组合[1－2]。将危岩体后部贯通或断续贯通且力学强度较低的带定义为主控结构面，其非线性失稳扩展是危岩破坏失稳的根本原因[1－4]。根据失稳模式，可将危岩分为坠落式危岩、倾倒式危岩和滑塌式危岩，危岩发育遵循链式规律[5－7]，并探讨了危岩链式崩落的静力学关系[8]。目前危岩崩塌研究已由静力学范畴进入动力学发展阶段。

岩体与应力波的相互作用机理已有相应研究，茹忠亮等[9]对弹性波在不同粗糙程度节理面的传播性质进行了研究;Li等[10]针对线弹性节理岩体建立了P波斜入射情况下波的传播方程;Zhao等[11]提出了应力波穿过多层节理的非线性模型;Resende等[12]分析了应力波在裂隙岩体中的衰减规律;Sarkar等[13]研究了纵波在冈瓦纳系岩体中的传播速度和衰减性能。

Nikitin等[14]分析了不同特征岩体在弹性波作用下将表现出特定的波场特征，Ju等[15]模拟岩体在波动力作用下的变形、破坏、能量耗散等机理，Kahraman等[16－17]研究了弹性波在岩体内传播时波速变化特征。本文应用波动力学和断裂力学方法分析危岩崩落对相邻危岩块产生的激振效应，量化激振作用对危岩稳定性的影响程度，为深入分析危岩破坏及崩落机制提供科学依据。

1 危岩崩落激振模型

危岩失稳崩落的主要原因是在岩体内部积累损伤，在自重与其他自然、人为因素的作用下产生卸荷裂隙，主控结构面突发性失稳断裂而致灾。针对坠落式危岩(图1)，建立危岩崩落激振模型(图2)

图1 坠落式危岩图Fig.1 Falling perilous rock

图2 危岩崩落激振模型Fig.2 Falling excitation model of perilous rock

由于危岩临空结构面引起危岩块张应力，裂隙竖向发育，群发性崩塌时的破坏面位置与起始危岩块的断裂面几乎位于同一竖向位置[18]。

基本假定:

(1)各层之间胶结强度相对较低，可忽略不计，危岩体之间只有压应力;

(2)危岩块崩落时产生激振波竖直向上和水平向山体内传播;

(3)由危岩体组成的边坡属于线弹性介质。

图2中，岩腔顶层1#危岩块是整个危岩发育的关键。1#危岩块崩落产生激振波水平向山体内和竖直向上传播时对邻近的2#和3#危岩块产生一定的损伤甚至诱发其失稳。主控结构面处为介质特征突变部位，两种介质的波阻抗不同，在界面处激振波将发生反射和透射。以波的局部场特征定理为基础，把任意形状波入射在弯曲界面上的透反射问题看成是平面波在界面上的透反射问题以展开研究。

2 激振波正入射条件下主控结构面受力分析

弹性波入射到主控结构面上将产生反射波和透射波(图3)，设结构面右侧为介质 i，其波阻抗为(ρvp)i，左侧介质 j，其波阻抗为(ρvp)j。

图3 弹性波在介质分界面上的反射和透射Fig.3 Reflection and transmission of elastic wave on dielectric interface

激振波垂直入射时不产生反射横波和透射横波，本文主要考虑纵波的透反射情况。在主控结构面两侧取两个相邻界面质点M和N，当入射波振面到达界面右侧时，由波面上相容条件可求得M质点的速度增量:

式中:σI为入射波强度(Pa);ρ为介质密度(kg/m3);vp为激振P波波速(m/s)。

当入射波反射后，M质点获得的速度增量:

式中:σR为反射波强度(Pa)。

在界面的左侧，透射波通过N质点获得速度:

式中:σT为透射波强度(Pa)。

在界面两侧满足质点位移连续条件和应力连续条件:

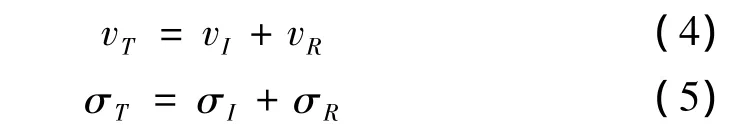
将式(1)～式(3)分别代入式(4)－式(5)得:

由波动理论，P波传播方向岩体的应变ε满足:

式中:Cp是介质质点位移速度(m/s)。

根据Hooke定律:

式中，σd为正应力(kPa);E为弹性模量(kPa)。则:

假定波在岩体中的震动为谐和震动，介质质点的位移速度C与其加速度a(m·s－2)和频率f(Hz)满足:

将式(11)代入式(10)得:

将式(12)代入式(6)得反射波强度:

将式(12)代入式(7)可得透射波强度:

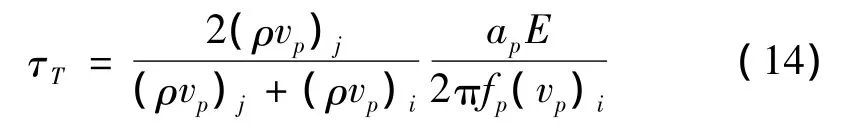
由图2，应力波水平传播时，1#危岩块崩落后产生的激振波在2#危岩块右部D结构面产生反射作用，假定结构面处反射波应力均匀分布，沿图2主控结构面D取出单元体(图4)。

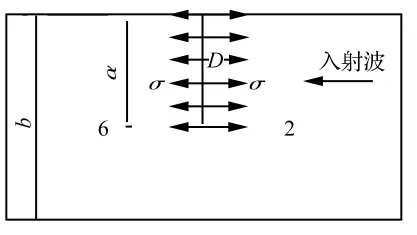
图4 激振波反射作用的主控结构面Fig.4 Dominant fissure under the action of reflection of excitation wave

图5 激振波对主控结构面的剪应力Fig 5 The shear stress of the excitation wave to the dominant fissure

激振波水平向山体内正入射条件下危岩主控结构面D所受反射力由式(13)和图4:

由图2，应力波竖直向上传播时，1#危岩块崩落后产生的激振波通过2#危岩块透射过结构面C，所产生透射波对结构面B产生剪应力，沿图2主控结构面C取出单元体(图5)。

激振波竖直向上传播时透射过结构面C对主控结构面B作用的剪应力由式(14)和图5:

3 激振作用下危岩稳定性断裂力学分析

根据最大周向应力准则第一基本假设[19]:裂纹的扩张沿着具有最大周向应力σθmax的截面开裂。该截面与主控结构面之间的夹角为主控结构面的断裂角θ0，取距裂纹尖端一微小距离r=r0的圆周上各点的周向应力σ0为研究对象。可知，裂纹扩展时断裂角θ0取决于下式:

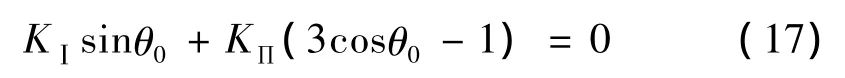
式中，KⅠ为第一类应力强度因子为第二类应力强度因子

求解式(17)可得:

由最大周向应力准则可知[19]，复合裂纹的联合应力强度因子为:

根据KⅠ和KΠ并将式(18)代入式(19)可求得联合应力强度因子Ke。根据主控结构面联合应力强度因子和危岩完整岩石断裂韧度建立危岩稳定性系数的断裂力学表达式[20]:

式中:Ke由不同工况下危岩体在不同荷载组合下进行求解;断裂韧度KⅠC为完整岩石的断裂韧度。

分别求出不考虑激振作用(天然状态和暴雨状态)下的危岩稳定性系数(Fs1)和考虑激振作用(天然状态和暴雨状态)危岩稳定性系数(Fs2)，求得危岩崩落激振作用对危岩稳定性的贡献率:

式中:ΔFs为 ΔFs1与 ΔFs2之差值。

4 激振作用下主控结构面应力强度因子

4.1 激振波水平入射的断裂力学分析

岩腔顶层起始岩块崩落诱发激振波所产生的激振脉冲穿过主控结构面时，因两侧介质特征存在差异，在界面处将产生反射力和透射力，将影响主控结构面处应力强度因子。

由图4分析可知起始岩块崩落时，在2#危岩块主控结构面D处由激振波反射力作用下应力强度因子为:

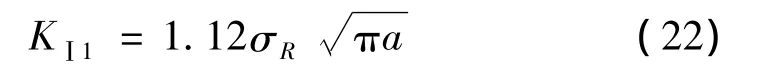
代入式(15)得:

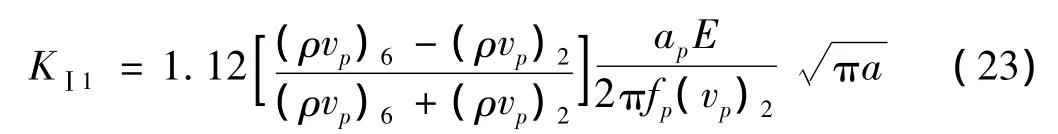
危岩主控结构面端部荷载除激振作用的影响因素外，还表现在危岩体自重所产生的弯矩和裂隙水压力所产生的张拉应力，沿图2主控结构面D取出的单元体，还可分解为另外两种情况，即仅由弯矩作用(情况1、图6)和仅由裂隙水压力作用(情况2、图7)

图6 弯矩作用的主控结构面图Fig.6 Dominant fissure under the action of bending moment

图7 裂隙水压力作用的主控结构面Fig.7 Dominant fissure under the action of crack hydraulic pressure

对于情况1，主控结构面D处由弯矩引起的应力强度因子KⅠ2[20]为:

式中:

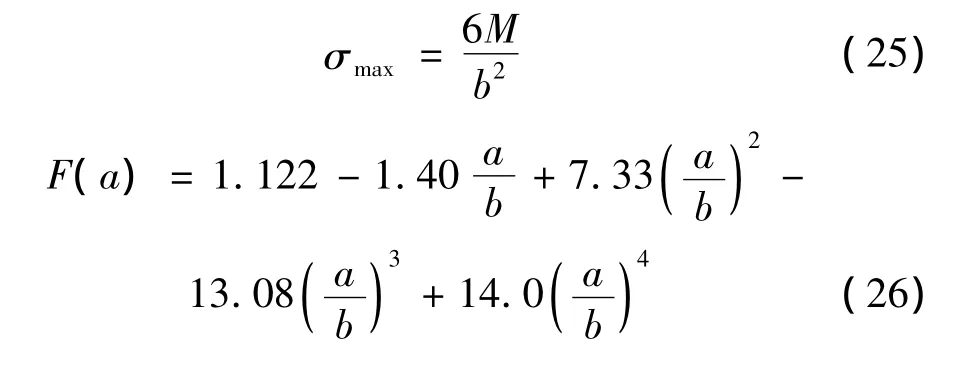
式中:F为最小二乘法经验公式求得的应力修正因子;σmax为主控结构面尖端最大应力(kPa)。

对于情况2:假定裂隙水压力在主控结构面贯通段均匀分布，则由此产生的应力强度因子KⅠ3

[20]为:

式中，γw为水容重(9.8 kN/m3);e1为主控结构面内充水深度(m)，天然状态下e1取主控结构面贯通段1/3，暴雨状态取 2/3[20]。

以上三种情况下，KΠ均为0，则式(19)可简化为:

将式(23)、式(24)和式(27)代入式(29)，可求得激振波作用下主控结构面的联合应力强度因子为:

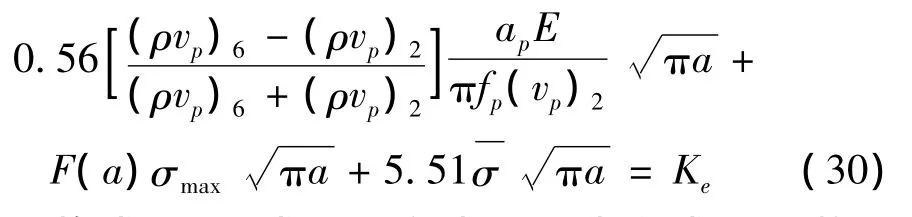
分别将式(25)、式(28)和式(26)代入式(30)整理可得:

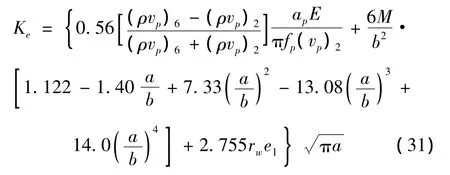
4.2 激振波竖直入射的断裂力学分析

由图5分析可知起始岩块崩落时，临近岩块主控结构面B处受激振波透射力作用，其应力强度因子KΠ[19]为:

联合式(16)得:

危岩主控结构面端部荷载还表现在危岩体自重所产生的弯矩和裂隙水压力所产生的张拉应力，沿图2主控结构面B取出的单元体(图8)。

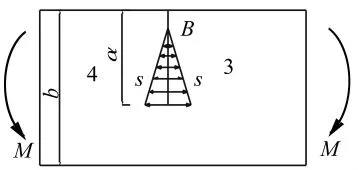
图8 裂隙水及弯矩作用下的主控结构面Fig.8 Dominant fissure under the the action of bending moment and fissure water

同理推导，裂隙水压力及弯矩对应力强度因子的贡献同式(24)和式(27)，由应力强度因子叠加原理:

将式(24)和式(27)代入式(34)得:

将式(33)和式(35)代入式(19)可得主控结构面联合应力强度因子为:

5 算例

綦江羊叉河陡崖位于三峡库区重庆市綦江县南部，地处背斜核部，陡崖由灰岩和泥岩构成，呈现显著的倒台阶状地貌形态。陡崖高差34～36 m，岩层由近于水平的灰岩和泥岩互层，下部泥岩厚约20 m左右，夹4.3 m灰岩，灰岩上部泥岩出露处发育高约5 m左右、深约3 m的岩腔，灰岩下部泥岩出露处为宽缓的侵蚀平台，宽约25 m左右，松藻矿区铁路从该平台通过[5]。区内危岩带底部为泥岩构成的软弱基座，由于抗风化能力相对较弱，常形成深浅不一的岩腔，上部危岩体主要为近直立的灰岩体，相关物理力学参数如表1[5]。

表1 羊叉河危岩体物理力学参数Tab.1 Physical and mechanical parameters of Yangcha River perilous rock

羊叉河危岩带的危岩体危岩W10崩落而至的激振波以正入射波对危岩W11、W12稳定性特征进行了断裂力学分析(图9)。C=a/(2πf)为激振波引起危岩体质点的振动速度，根据不同的工况取值不同，本文取值为30(mm·s－1)作为计算值[21－22]，计算结果如表2 所示。

图9 羊叉河危岩W11、W12危岩Fig.9 W11#and W12#perilous rock of Yangcha River

表2 羊叉河W11#和W12#危岩计算表Tab.2 Calculation table for W11#andW12#perilous rock of Yangcha River

表2为羊叉河W11#和W12#危岩，在天然和暴雨两种工况，分别计算了不考虑激振效应和考虑激振效应的的危岩应力强度因子值，结果表明:考虑危岩崩落激振波效应后，危岩应力强度因子值在天然和暴雨两种工况下都有明显的增长趋势，崩落激振波以竖直平方传播比水平方向向山体里传播影响大得多，竖直方向增长了10%左右，水平方向增长了2%左右。其研究成果对实施危岩防灾减灾提供了重要的科学依据。因此，对于坠落式危岩，群发性崩落现象常竖向发育，应特别重视下部危岩块崩落时对上部岩体块的激振效应。

6 结论

(1)群发性危岩崩落考虑危岩体之间的相互作用十分重要。针对坠落式危岩，提出了危岩崩落激振计算模型。分析了危岩崩落激振波正入射条件下危岩主控结构面的受力特征，建立了激振作用下危岩体主控结构面尖端联合应力强度因子计算式。

(2)危岩崩落时的激振波对危岩体稳定性影响的大小与起崩危岩块自身特征、危岩体弹性模量、泊松比、岩体密度等参量有关。当危岩体主控结构面两侧弹性模量、泊松比、岩体密度等物理力学参数相差越大，激振效应越明显。

(3)实例分析表明，考虑危岩崩落激振作用后，危岩稳定性系数在天然和暴雨两种工况下都有明显降低趋势，崩落激振波以竖直平方传播比水平方向山体里传播影响要大得多，竖直方向降低10%左右，水平方向降低2%左右。根据危岩崩落激振作用对危岩稳定性的贡献率特征可知，激振波极易诱发接近临界状态的危岩体失稳，出现危岩的群发性崩落。因此在工程治理及危岩稳定性的计算中应恰当考虑激振波对危岩体的失稳效应。

[1]Chen H K，Tang H M，Ye S Q.Research on damage model of control fissure in perilous rock[J].Applied Mathematics and Mechanics，2006，27(7):967 －974.

[2]唐红梅，王林峰，陈洪凯，等.软弱基座陡崖危岩崩落序列[J].岩土工程学报，2010，32(2):205－210.

[3]Braathen A，Blikra L H，Berg S S，et al.Rock-slope failure in Norway;type，geometry，deformation mechanisms and stability[J].Norweigian Journal of Geology，2004，84:67 －88.

[4]Chen H K，Tang H M，Zhu H.Reserch on duration for perilous rock to form[J].Wseas Transactions on Aaalied and Theoretical Mechanics，2006，1(2):169 －173.

[5]陈洪凯，唐红梅，王林峰，等.危岩崩塌演化理论及应用[M].北京:科学出版社，2009.

[6]陈洪凯.三峡库区危岩链式规律的地貌学解译[J].重庆交通大学学报(自然科学版)，2008，27(1)，91－95.

[7]陈洪凯，唐红梅，王林峰，等.缓倾角岩质陡坡后退演化的力学机制[J].岩土工程学报，2010，32(3)，468－473.

[8]王林峰，陈洪凯.危岩链式规律的力学演绎[J].重庆建筑大学学报，2008，30(2):94－97.

[9]茹忠亮，蒋宇静.弹性纵波入射粗糙节理面透射性能研究[J].岩石力学与工程学报，2008，27(12):2535－2539.

[10]Li J.Ma G.Analysis of blast wave interaction with a rock joint[J/OL].Rock Mechanics and Rock Engineering，2009[2010－6－24].

[11]Zhao X B，Zhao J，Cai J G，et al.UDEC modeling on wave propagation across fractured rock mass[J].Computers and Geotechnics，2008，35(1):97－104.

[12]Resende R，Lamas L N，Lemos J V，et al.Micromechanical modelling of stress waves in rock and rock fractures[J/OL].Rock Mechanics and Rock Engineering，2010[2010 －6 －24 ]. http://www. springerlink. com/content/k56757121884u753/fulltext.html.

[13]Sarkar R K，Singh O P.Study of P-wave velocities and attenuation coefficients of gondwana rocks from chandawardha valley coalfield[J].Maharashtra，India，2006，54(3):250－259.

[14]Nikitin A N，Ivankina T I，Ignatovich V K.The wave field patterns of the propagation of longitudinal and transverse elastic waves in grain-oriented rocks[J].Physics of the Solid Earth，2009，45(5):424－436.

[15]Ju Y，Wang H J，Yang Y M，et al.Numerical simulation of mechanisms of deformation，failure and energy dissipation in porous rock media subjected to wave stresses[J].Technological Sciences，2010，53(4):1098 －1113.

[16]Kahraman S，Yeken T.Determination of physical properties of carbonate rocks from P-wave velocity[J].Bull Eng Geol Environ，2008，67(1):277 －281.

[17]Schubnel A，Benson P M，Thompson B D，et al.Quantifying damage，saturation and anisotropy in cracked rocks by inverting elastic wave velocities[J].Pure appl.Geophys，2006，163(5－6):947－973.

[18]陈洪凯，鲜学福，唐红梅.石质山区崩塌灾害形成机制[J].四川大学学报(工程科学版)，2010，42(3):1－6.

[19]洪起超.工程断裂力学基础[M].上海:上海交通大学出版社，1986:55－58.

[20]陈洪凯，鲜学福，唐红梅.危岩稳定性断裂力学计算方法[J].重庆大学学报，2009，32(4):434－437.

[21]Sambuelli L.Theoretical derivation of a peak particle velocity-distance law for the prediction of vibrations from blasting[J].Rock Mech Rock Eng，2009，42(3):547－556.

[22]肖 望，周绍武，王爱兴，等.裂隙结构面对爆破振动速度传播规律的影响分析[J].爆破，2010，27(1):89－91.

[23]黄 雨，孙启登，许 强.滚石运动特性研究新进展[J].振动与冲击，2010，29(10):31 －35.

[24]汪 敏，石少卿，康健力.落石冲击作用下环形耗能性能的理论及数值模拟研究[J].振动与冲击，2011，30(3):10－13.