山地风场中特高压输电塔线体系动力可靠度研究
李正良,韩 枫,张春涛,范文亮,孙 毅
(1.重庆大学 土木工程学院,重庆 400045;2.重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045)
随着我国西电东送战略的实施,目前投入运营的500 kV以上的高电压输电线路已经达6 000多公里[1-3]。作为大型复杂的重要生命线工程,特高压输电塔线体系与普通输电塔线体系相比,具有塔体结构高、跨度大和电压等级高等特点[4-6],对风荷载作用响应十分敏感,容易发生风振动态坍塌,给人民生活及国民经济带来不良影响和巨大损失。因此,随着电力行业的快速发展随机风荷载作用下输电塔线体系动力响应及其可靠度的研究日益突出,为减少或避免由此带来的灾害,必须建立正确评估风荷载作用下输电塔线体系的动力可靠度分析方法。
风荷载的随机性及其经过高耸结构产生复杂的气流分离等因素致使高电压输电线体系的风振响应十分复杂,受到了国内外学者较为广泛的研究。Ballio等[7]在对108.6 m高的正六边形塔体进行风振实测时,发现了塔体横风向响应略大于顺风向响应,Glanville等[8]亦通过对正方形塔体进行风振实测研究,验证了Ballio的研究成果;Hiroshi[9]对 500 kV 输电塔线体系进行了风洞试验研究,得到了输电塔体所受组合荷载达到最大的最不利风向角和横向风力系数最大角,有效地降低了后续研究的难度,极大地减少了计算量;程志军等[10-11]通过风洞试验研究了不同风向、风速条件下输电塔的风振响应,并对塔线体系的耦合作用进行了定性分析,与Momomura[12]经三年实测得到塔线体系耦合作用的成果相符;李正良等[13-15]首次对1 000 kV汉江大跨越输电塔线体系进行了风洞试验研究,在对输电塔体风振响应及等效风荷载进行深入分析的基础上,提出了输电塔动力计算简化模型,并对输电塔耦合抖振的有限元CQC法、SRSS法和虚拟激励法进行了修正。不难发现,上述研究均是在实测和试验的基础对输电塔的风振响应进行了研究,亦得到了较为显著的研究成果,为后续研究打下了良好基础。目前,随机风荷载作用下输电塔的受力、变形及破坏特征等方面的研究虽已取得了许多定性的研究成果,但是对输电塔在随机风荷载作用下发生应力比、曲率、位移等动力响应超越其最大限值进入不安全域的出现概率等研究显著偏少。虽然,张琳琳等[16]通过概率密度演化方法和动力可靠度分析法对输电塔的动力可靠度进行了研究,但该研究只是以高度仅为54.96 m的猫头塔为对象对一般随机风荷载作用下概率密度演化方法和动力可靠度分析法进行了验证,并未对输电塔体的动力特征及其可靠度受风场影响的变化规律等做出详细研究。
然而,我国地形复杂多变,国土面积的70%均为山地地形,与一般平地地形不同,山地地形必然对近地风场造成较大影响,这对输电塔的安全性能提出了新的要求[13]。并且,实际工程中特高压输电塔因电压高、跨度大等常建在地势较高的山坡或江河两边较高的山顶,致使整个服役期均处于受山地地形影响的风场中。为此,文中在风洞试验的基础上对不同坡度和不同高度的单个山体以及不同遮挡间距的两个山体的风场分别进行了研究,并基于试验数据对特高压输电塔线体系在各工况的风场条件下分别进行动力时程分析。最后,采用随机结构动力可靠度计算方法对各工况下输电塔的动力可靠度分别进行了研究。
1 山地风场特性风洞试验
1.1 风洞试验概况
本次复杂山体表面风场特征测试试验在中国空气动力研究与发展中心低速所的FL-11风洞进行,风洞截面尺寸为1.4 m ×1.4 m,试验段长为6.3 m。试验几何模型缩尺比为1∶1 000,风速缩尺比约1∶2.5。试验数据利用DSM3400电子扫描阀系统进行采集,采样频率为156 Hz,每个测点采用时间步数为4 096步,排管高0.7 m,沿其高度平均分布20根探针,如图1所示。

图1 山地风场风洞试验Fig.1 The wind tunnel test of hilly terrain wind field
试验中常用于模拟山体形状的各模型表达式如式如下:
三角形:

钟形:

高斯形:
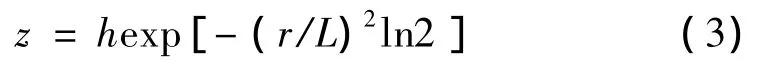
余弦平方形:

式中,r在不同山体模型中表达式不同,二维山体中相当于横坐标x,在三维山体中则等于,C 为山体三维形状常数;h为山体高度,L为山顶到h/2处的水平距离,各参数几何意义见图2。

图2 山体形状示意图Fig.2 Schematic diagram of hill
试验中风速加速效应随山体形状不同而出现显著差异[17],但实际山地的复杂性远非式(1)~式(4)所示的几个简单模型所能全面模拟。因此过分注意山体形状并无太大实际意义,试验中可取各种山体模型试验结果的平均值进行研究,或者仅对某一种山体模型进行研究[18],而不必过分深究山体形状对风场的影响。为此,本次试验基于第二种方法仅选取余弦平方型山体模型模拟山地地形,三种山地地形的不同试验工况分别为:① 单个山体坡度变化 S1 ~S8,即 1.00、0.75、0.60、0.50、0.43、0.38、0.33、0.30;② 单个山体高度变化H1~H3,即100 mm、150 mm和200 mm;③两个山体间距离变化为 L1 ~L5,即 0、200 mm、400 mm、600 mm和800 mm。各工况平均风速均为15 m/s,并采集顺风向山脊上5个关键位置和下风向5个典型位置风剖面的风速时程,如图3所示。
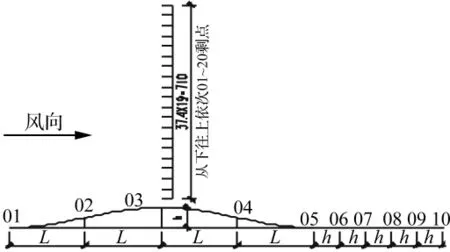
图3 试验测点位置Fig.3 Distribution of test measuring points
1.2 试验结果分析
1.2.1 山体坡度变化试验结果
山地地形中某高度平均风速比相对于平地的同一高度的平均风速有所增加,一般在山顶的近地面增加最为明显。因此,研究山地风场时常用无量纲参数即加速比来定量描述加速效应,表达式为:

式中,U(z)为山地地面以上z高度处的风速,U0(z)为平地地面以上z高度处的风速。
不同山体坡度对风场影响的试验结果如图4所示。迎风面近地平均风加速比随坡度变化最小,基本趋于零,但试验中随测点位置高度增加平均风加速比逐渐增大,如位置02处最低测点的加速比已经达到0.4,但随坡度增加相同测点加速比变化不大;图4(a)中亦给出了迎风面湍流度变化曲线,不难发现,山体坡度对迎风面山坡湍流度及其空间分布几乎没有影响。山顶平均风加速比与背风面和迎风面的加速比相比最大,由图4(b)可知其最低测点平均风加速比达0.6,并且随坡度略有增加,但山顶风速湍流度与迎风面相似基本不受山体坡度影响。图4(c)则反映出背风面各测点位置的平均风加速比变化较大,并且同一测点位置上部探针所测加速比均随坡度增加而保持不变,但底部探针所测加速比则随坡度增加而明显减小,在坡度为1时加速比已基本达到-1.0,由此可见随坡度增大流动分离越容易在背风面山腰产生,最后形成涡旋,而中心风速为0。随测点位置离山体的距离增加,山体对平均风场的影响亦越小,位置10处已基本没有影响。同时,背风面各坡度下湍流度的分布曲线在山体高度处出现“分岔”,随下风向距离的增加,“分岔”点逐步增高。

图4 不同山体坡度对风场的影响Fig.4 Effect of slope on wind field
1.2.2 山体高度变化试验结果
同一坡度不同山体高度的迎风面、山顶及背风面最大平均风速加速比如表1所示,对比分析可知:迎风面山体表面加速比最大值均较小,风场的平均风特性较为稳定;山顶加速比则随山体高度增加,近地面加速比显著提高,并且距离地面同一高度的加速比随山体高度增加而增大,但当距地面121 mm以上加速比已几乎不受山体高度的影响;试验中背风面加速比受离地高度和测点位置的不同变化较大,山体越高背风区影响范围越大,但同一高度测点随山体高度越高,加速比却越小。同时,图5亦分别给出了迎风面、山顶及背风面的湍流度,距地面越近湍流度越大。迎风面和背风面的近地面湍流度相对较大,尤其是背风面最大湍流度达0.4,并且随山体高度增加湍流度增大,但山顶湍流度几乎不受山体高度影响。
山地风场研究中关于山体高度对山顶和背风面平均风加速比的影响,可通过高度修正因子进行修正。
山顶:

背风面:
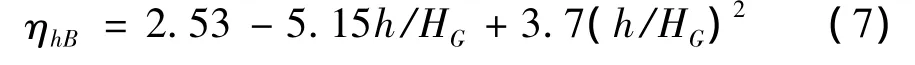
同时,山体高度对脉动风的影响亦可通过下式进行考虑:
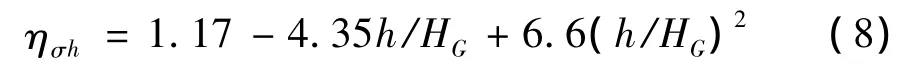
式中,h为山体高度,HG为梯度风高度。

表1 山体高度对最大加速比的影响Tab.1 Effect of hill height on maximum speed-up ratio

图5 山体高度对风场的影响Fig.5 Effect of height on wind field
1.2.3 山体间距变化试验结果
同一坡度及高度情况下,不同山体遮挡间距对迎风面、山顶和背风面平均风及湍流度的影响程度随高度的变化情况如图6所示。图6(a)中两山体迎风面测点位置随山体距离增加,可近似为单个山体时不同位置的情况,所以随下风向距离增加,山体对平均风剖面的遮挡效应越小;同理,随山体间距增加,迎风面湍流度越小,山体遮挡效应亦不明显;但无论平均风还是湍流度在距离地面200 m以上时几乎均不受遮挡山体的影响,曲线趋于直线。图6(b)中山顶平均风速及湍流度受遮挡间距影响较小,并且在离山顶100 m高度以上各曲线重合,平均风和湍流度亦未发生明显变化。图6(c)则给出了背风面平均风及湍流度随山体遮挡间距以及离地面高度的变化情况,随山体间距离增加,第二个山体背风面平均风速减小,但试验中减小幅度随测点位置距离增大而减小,直到位置10时遮挡间距的影响基本可以忽略;背风面湍流度随山体遮挡间距离增大而增大,试样中位置06和07增加最显著,但其后测点与平均风变化情况相同,随距离增加逐渐减小,到位置10时几乎可以忽略。
综上所述,山体之间遮挡间距对山背风面风场存在较大影响,但山顶的风场几乎均不受遮挡山体影响。为此,研究中背风面风场受山体遮挡间距的影响可由实验数据拟合的修正系数进行修正:
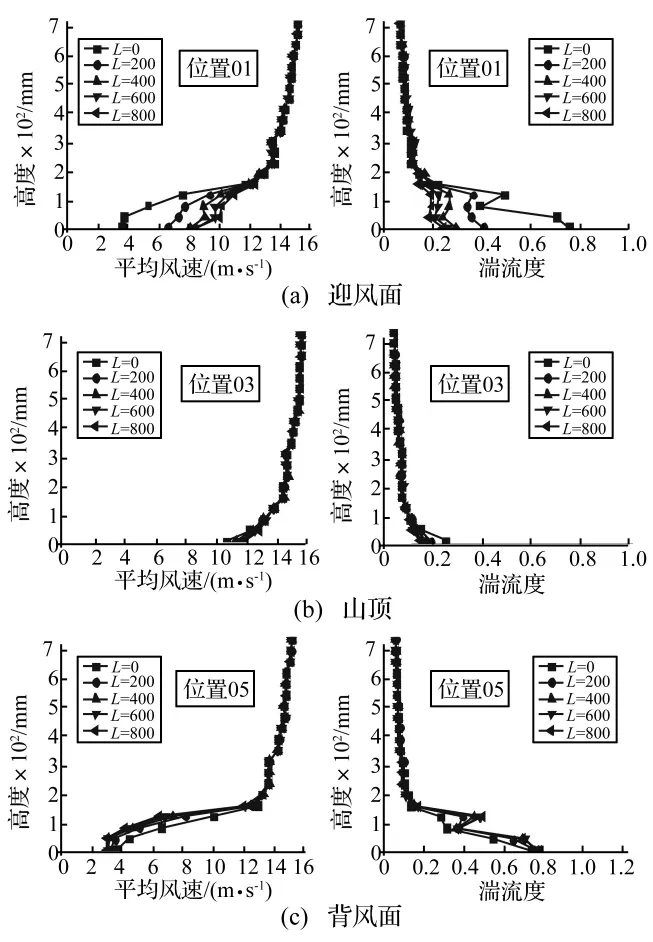
图6 山体间距对风场的影响Fig.6 Effect of distance between hills on wind field

式中,d1为遮挡距离,HG为梯度风高度,i为山体坡度,即 i=h/L1,h,L1几何意义同图 2。
脉动风加速比修正系数:

2 特高压输电塔线体系动力可靠度分析
2.1 动力可靠度计算方法
随机荷载作用下结构的运动方程为:

式中:X为随机参数向量表示结构参数或荷载参数中的随机因素,M、C和K分别表示结构的质量、阻尼以及刚度矩阵和v分别为结构的加速度、速度以及位移向量,f(X,t)为动力激励。
令Z(t)表示结构位移、速度、加速度和应力等响应的n维矢量随机过程,则:

在时间段(t0,t0+ΔT)内,若Z(t)的任一元素超越对应的临界值(i=1,…,n),则结构失效。显然,结构的功能函数可表示为:

因为,Zi(X,t)为结构各响应构成的n维矢量随机过程,于是,结构的失效概率可表示为:
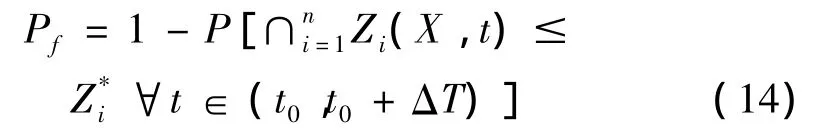
若假设随机变量:

则式(14)可表示为:

本文所研究的动力可靠度问题是建立在首次超越破坏的机制上,即结构动力响应Zi不超过的总概率。为此,当较高时,可以假定不同事件超越界限值是相互独立的。于是,对于研究对象为单个事件时,且t0=0,t=ΔT的时间段内,式(16)可表示为:

例如,当以随机荷载作用下结构的位移v(t)为研究对象时,式(17)可以进一步的表示为:
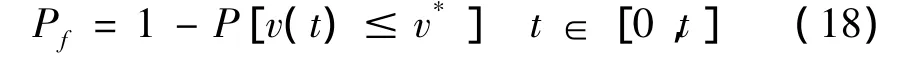
式中,v*为阀值即输电塔体顶部限制位移。
2.2 计算结果分析
基于工程实例及风洞试验[1-3],取某特高压大跨越输电塔为研究对象,如图7所示。塔体为108 m高的直线塔,计算中将塔体简化为11节段,各模型节段参数如表2所示。

图7 特高压输电塔分段示意图Fig.7 The schematic diagram of UHV transmission tower segments
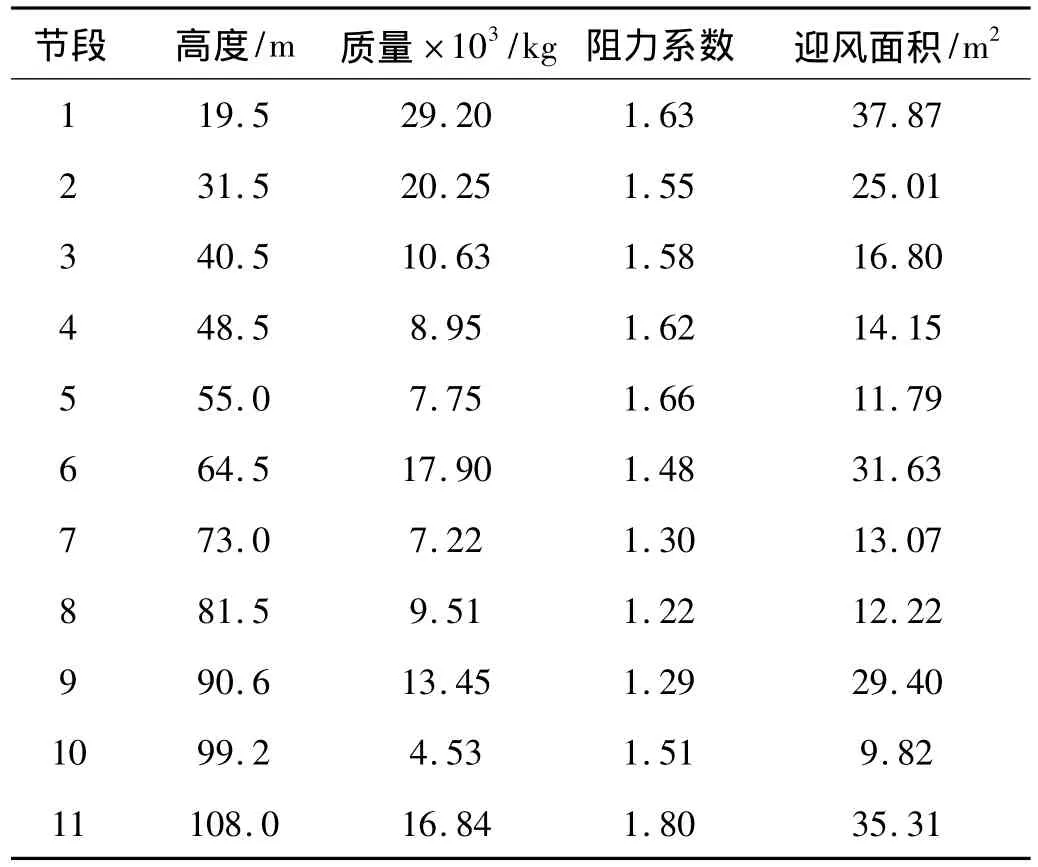
表2 塔体节段模型参数Tab.2 The parameters of the transmission tower segments
首先,根据第1节中试验数据模拟出相应风场,并通过有限元计算理论在各风场条件下分别对输电塔线体系进行动力时程计算。对于第一类山地地形的各工况可通过试验数据直接模拟各风场,对于第二、三类山地地形的各工况则既可根据试验数据,亦可采用式(6)~式(10)对平均风和脉动风加以修正。第二类山地地形中各工况下01位置输电塔顶部位移如图8所示。

图8 第二类地形下迎风面输电塔顶部位移时程Fig.8 The displacement time-history curves of the tower top on windward in the 2ed hilly terrain
然后,取阀值为0.2 m,利用式(18)计算出不同工况下迎风面、山顶及背风面各塔顶位移超越阀值的失效概率,从而可得各风场条件下输电塔顶部位移的动力可靠度,如表3所示。显然,由表中各数据可知不同工况下输电塔顶部位移不超越阀值的可靠度均受各工况条件下山地地形的影响。第一类山地地形中,各测点输电塔可靠度随山体坡度增加而减小,背风面山脚输电塔动力可靠度相对最小,但随下风向的距离增加影响逐渐降低,可靠度相应增加;第二类山地地形中,山体高度对输电塔可靠度影响较大,山体越高背风面山脚近地风脉动特性越显著,输电塔体风振响应随机性越大,可靠度越低;第三类山地地形中,各工况下迎风面和山顶输电塔可靠度未出现明显变化,但随遮挡间距增加背风面脉动特性相对增大,输电塔可靠度亦随之减小。综上所述,三类山地地形中背风面山脚风场受山地地形影响较大,脉动特性显著,输电塔动力可靠度相对最小,但随下风向距离增大影响逐渐减小可靠度随之增加,因此输电塔选址时应尽力避免主风向山体背风面山脚位置。

表3 各山地风场下特高压输电塔的可靠度(%)Tab.3 The reliabilities of UHV transmission tower under different hilly terrain wind field(%)
3 结论
本文通过风洞试验对三类山地地形的平均和脉动风特性进行了研究,在试验数据的基础上采用有限元理论计算出特高压输电塔在各风场条件下的动力响应,并利用随机结构动力可靠度计算方法分别计算出各风场中输电塔的动力可靠度。主要结论如下:
(1)与平地风场相比,山地地形中的平均风和脉动风存在较大区别。坡度对迎风面和山顶风场的平均风和脉动风影响较小,但背风面的风场特性受坡度影响很大,坡度越大平均风和脉动风的变化越显著;山体高度对迎风面和山顶的平均风影响小,但迎风面近地脉动风却随山体增加影响相对增大,而山体高度对背风面的风场的影响相对较大;山体之间遮挡间距对山体背风面山脚近地风场存在较大影响,但山顶风场几乎均不受遮挡山体影响。
(2)通过试验数据拟合出了山体高度和两山体之间遮挡间距对山顶和背风面平均风和脉动风加速比的修正系数表达式,在后续山地风场的模拟计算中相对降低了计算难度和提高了计算效率。
(3)三类山地地形中背风面山脚风场受山地地形影响最大,输电塔动力响应的随机性随之增加,致使各工况中背风面输电塔动力可靠度相对最小,但随下风向距离增加影响程度逐渐减小,可靠度随之提高;迎风面和山顶输电塔动力可靠度变化较小。
[1]肖正直.特高压输电塔风振响应及等效风荷载研究[D].重庆:重庆大学,2009.
[2]汪之松.特高压输电塔风振响应及风振疲劳性能研究[D].重庆:重庆大学,2009.
[3]李正良,肖正直,韩 枫,等.1 000 kV汉江大跨越特高压输电塔线体系气动弹性模型的设计与风洞试验[J].电网技术,2008,32(12):1-5.LI Zheng-liang,XIAO Zheng-zhi,HAN Feng,et al.Aeroelastic model design and wind tunnel tests of 1000 kV Hanjiang long span transmission line system[J].Power System Technology,2008,32(12):1 -5.
[4]汪之松,李正良,肖正直,等.1 000 KV双回路特高压输电塔等效静风荷载研究[J].电网技术,2009,33(14):6 -12.WANG Zhi-song,LI Zheng-liang,XIAO Zheng-zhi,et al.Equivalent along-wind direction static wind load of transmission tower for 1000 kV double circuit transmission lines on same tower[J].Power System Technology,2009,33(14):6-12.
[5]韩 枫,肖正直,李正良,等.1000kV汉江大跨越输电塔线体系三维脉动风场模拟[J].高电压技术,2009,35(9):1000-1004.HAN Feng,XIAO Zheng-zhi,LI Zheng-liang,et al.3D Stochastic wind field simulation of 1000kV Hanjiang long span transmission line system[J].High Voltage Engineering,2009,35(9):1000-1004.
[6]楼文娟,孙炳楠,叶 尹.高耸塔架横风向动力风效应[J].土木工程学报,1999,32(6):67-71.LOU Wen-juan, SUN Bing-nan, YE Yin. Across-wind dynamic response of tall latticed tower[J].China Civil Engineering Journal,1999,32(6):67 -71.
[7]Ballio G,Meberini F,Solari G.A 60 year old 100m high steel tower:limit states under wind action[J].Journal of Wind Engineering and Industrial Aerodynamics,1992,41 -44:2089-2100.
[8]Glanville M J,Kwok K C S.Dynamic characteristics and wind induced response of a steel frame tower[J].Journal of Wind Engineering and Industrial Aerodynamics,1995,54 -55:133-149.
[9]Hiroshi K.Wind tunnel test on 500kV transmission tower with solid web brackets[J].Journal of Wind Engineering,1994,58:54-60.
[10]程志军,付国宏,楼文娟,等.高耸格构式结构塔架风荷载试验研究[J].实验力学,2000,15(1):51-55.CHENG Zhi-jun,FU Guo-hong,LOU Wen-juan,et al.Research for the wind force on high-rise latticed tower[J].Journal of Experimental Mechanics,2000,15(1):51-55.
[11]付国宏,程志军,孙炳楠,等.架空输电线路风振试验研究[J].流体力学实验与测量,2001,15(1):16-21.FU Guo-hong, CHENG Zhi-jun, SUN Bing-nan, et al.Research for the wind-induced vibration of the overhead power transmission line system[J].Experiments and Measurements in Fluid Mechanics,2001,15(1):16-21.
[12]Momomura Y,Marukawa H,Okamura T,et al.Full-scale measurements of wind-induced vibration of a transmission line system in amountainousarea [J].JournalofWind Engineering and Industrial Aerodynamics,1997,72:241-252.
[13]李正良,魏奇科,孙 毅.山地地形对输电塔风振响应的影响[J].电网技术,2010,34(11):214-219.LI Zheng-liang,WEI Ji-ke,SUN Yi.Influence of mountain topography on response to wind-induced vibration of transmission tower[J].Power System Technology,2010,34(11):214-219.
[14]李正良,任 坤,肖正直,等.特高压输电塔线体系气弹模型设计与风洞试验[J].空气动力学学报,2011,29(1):102-106.LI Zheng-liang, REN Kun, XIAO Zheng-zhi, etal.Aeroelastic model design and wind tunnel test of UHV transmission line system [J].Acta Aerodynamica Sinica,2011,29(1):102-106.
[15]李正良,肖正直.基于高频天平测力试验的特高压输电塔等效风荷载研究[J].电网技术,2011,35(5):27-32.LI Zheng-liang,XIAO Zheng-zhi.Research on equivalent wind loadsofUHV transmission towerbased on high frequency force balance tests[J].Power System Technology,2011,32(12):27-32.
[16]张琳琳,李 杰.风荷载作用下输电塔结构动力可靠度分析[J].福州大学学报(自然科学版),2005,33:36-41.ZHANG Lin-lin,LI Jie.Dynamic reliability analysis of windinduced transmission tower[J].Journal of Fuzhou University(Natural Science),2005,33:36-41.
[17]Weng W,Taylor P A,Walmsley J L.Guidelines for airflow over complex terrain:model developments[J].Journal of Wind Engineering and Industrial Aerodynamics,2000,86:169-186.
[18]孙 毅.山地风场中超高层建筑风致振动研究[D].重庆:重庆大学,2010,4.

