基于MM-EMD的改进HHT及应用
梁 升,王新晴,王 东,夏 天,钱淑华
(1.解放军理工大学,南京 210007;2.海军工程研究设计局,北京 100841)
1 Hilbert-Huang变换的局限性
与小波等方法相比,虽然Hilbert-Huang变换(Hilbert-Huang Transform,HHT)是一种非先验的方法,但仍然假定信号由本征模态分量(Intrinsic Mode Function,IMF)和普通趋势项构成[1]。IMF满足两个条件:① 整个信号长度上极值点和过零点的数目必须相等或只差一个;② 在任意时刻,由极大值定义的上包络线和由极小值定义的下包络线的平均值为0。这两个条件实际上表示了一种波动的模式。如果被分析的信号仅仅由多个IMF分量与普通趋势项组成,那么,经验模态分解(Empirical Mode Decomposition,EMD)所得到的IMF分量大都具备明确的物理意义,HHT能取得较好的分析效果。而工程实际中,信号是由多种分量组合而成的,不是单纯的IMF分量与普通趋势项的结合,因而当信号中存在非普通趋势、非IMF分量时HHT分析的效果并不理想。图1所示方波信号是一种典型的、可能具有特定的物理意义的非趋势、非IMF分量。

图1 方波信号Fig.1 Square wave signal
2 广义趋势项
针对HHT方法存在的上述局限,提出改进思路:当原始信号中可能存在非IMF分量时,先将非IMF分量分离出来,再对剩余信号进行HHT分析。
EMD分解得到的趋势项一般为常数或单调函数。而工程实际中,系统在受到强大外力作用或内部结构发生巨大变化的情况下,相关的信号幅值或其他特征会发生急剧变化,从而使信号趋势产生渐变甚至突变,当外力作用或系统内部结构变化具有周期性时,相应的信号趋势也可能具有周期性。本文将信号中反映这种趋势的分量称为广义趋势项。广义趋势项与传统意义上的趋势项不同。在早期对时间序列的研究中,趋势项一直被看作时间序列长时间的动向,但是迄今为止,趋势项在数学上并没有一个准确的定义,一般认为,趋势项是测试信号中周期远大于信号记录时间长度的成分[3]。而广义趋势项主要反映了待测系统在外力、内力的综合作用下相应信号的主要变化动向,它既包括了传统意义上的趋势(长期趋势),也包括了部分短期趋势。广义趋势项不一定是IMF分量。

图2 实测夹紧缸工作过程中夹紧腔油压波动波形Fig.2 The oil pressure fluctuation signal under the periodic excitation

图3 原信号基于EMD分解重组后得到的三个分量Fig.3 The three components of the pressure signal based on EMD
与一般的机械振动加速度信号、地震加速度信号不同,液压系统内部的压力信号不是以零轴为中心的上下波动,而是随着系统状态、外部负载等因素的改变而逐渐变化,如果出现波动,也是以一定趋势为中心的上下波动。油压信号的广义趋势项就是由这些不同时段的相应趋势所构成的,它由系统状态、外部负载等因素决定,一般情况下不满足IMF分量的条件。以周期激励下的夹紧缸内油压波动信号(图2)为例,文献[2]运用传统HHT方法将其分解为受迫振动、自由振动的组合(图3),其受迫振动分量就是该信号的广义趋势项,而自由振动分量可以看作是以相应时刻受迫振动分量为中心的上下波动。以上自由振动与受迫振动分量都是通过EMD分解重组得到的。由前文知,EMD对于本身带有非IMF分量的信号,其分析效果会受到“IMF假设”的影响,如果先用某种方法分离出原始信号中不属于IMF分量的广义趋势项,再对剩余信号进行HHT分析,可能得到更好的分析效果。
3 基于MM-EMD的HHT改进算法
前人主要在以下两个方面对数学形态学(Mathematical Morphology,MM)与HHT的结合进行了研究:用数学形态滤波器对信号进行滤波降噪预处理,然后再进行HHT分析[4-5];先对信号进行 EMD 分解,再对筛选出的IMF分量进行基于数学形态滤波器的降噪处理[6]。
MM-EMD不同于以上方法,其基本思想是运用数学形态滤波器提取出不利于EMD分解的广义趋势项等低频非IMF分量,再对剩余信号分量进行EMD分解。具体步骤如下:
(1)对原信号 x(t)={x1,x2,…,xN}进行傅里叶变换,估计出自由振动信号最大频率fq。
(2)运用开-闭和闭-开组合形态滤波器处理信号[7-8],分离出广义趋势项 Xq(t)及余项 Xr(t)。数学形态滤波器的结构元素选用方形结构元素。根据fq与原信号的采样频率fs确定方形结构元素长度M=fsfq,当广义趋势项并不明显时,可令M=N/4。根据原信号x(t)自身特点,可以选取原始信号相邻数据之间差额绝对值中的非零最小值K作为结构元素的高度,即且 K≠0。
(3)对余项Xr(t)进行经验模态分解,得到若干IMF分量和一残量rn;
(4)运用相关系数法、互信息、频域特征等方法对IMF分量进行筛选,对筛选出来的IMF分量进行Hilbert谱分析。
需要说明四点:① 大量仿真与实测信号处理结果表明,与三角形、半圆形结构元素相比,方形结构元素提取信号突变特征特别是突变趋势的效果较好,因而以上过程选用方形结构元素;② 噪声与突变引起的信号相邻数据差值的绝对值远大于信号按自身规律变化时相邻数据差值的绝对值,原始信号相邻数据之间差值绝对值中的非零最小值K接近于信号按自身规律变化时相邻数据的最小差值,大量仿真试验表明,当平结构元素的高度选择为K时,可以有效提取出包含准确突变信息的趋势项,同时滤除一定程度的噪声特别是脉冲噪声;③ 自由振动信号最大频率fq可以根据实际情况进行修正;④ 如果其他方法也可以有效分离出广义趋势项,即可将以上步骤中的(1)、(2)改为采用其他方法,步骤(3)、步骤(4)不变。
4 实例
分别用传统HHT方法与基于MM-EMD的改进HHT方法对仿真信号与实测信号进行处理,检验新方法的分析效果。
4.1 仿真信号
仿真信号由频率为4 Hz的方波信号与间断产生的频率为50 Hz的正弦信号叠加而成,如图4所示,采样频率fs=2 000 Hz,采样点数N=2 000。对该信号进行EMD处理后得到六个IMF分量和一个残量。分别对各个分量进行Hilbert谱分析,最终得到与原始信号自相关系数最高的 c1分量的 Hilbert-Huang谱,如图5所示。

图4 仿真信号时域图Fig.4 Simulated signal

图5 仿真信号的传统HHT方法分析结果Fig.5 The analysis result of the simulated signal based on traditional HHT
原始信号中最高频率成分为50 Hz,因而取fq=50 Hz。方形结构元素长度M=fs/fq=40。根据原始信号可以计算出方形结构元素高度采用由此形态结构元素构成的开-闭和闭-开组合形态滤波器对原始信号进行形态滤波处理,得到广义趋势项Xq(t)与余项Xr(t),如图6(a),图6(b)所示。

图6 仿真信号的数学形态滤波结果Fig.6 The filtered result of simulated signal based on MM
对余项Xr(t)进行EMD处理,得到六个IMF分量和一个残量。分别对各个分量进行Hilbert谱分析,最终得到余项Xr(t)中与原始信号自相关系数最高的c1分量的Hilbert-Huang谱,如图7所示。

图7 仿真信号基于MM-EMD的改进HHT分析结果Fig.7 The analysis result of the simulated signal based on improved HHT by MM-EMD
对比图5与图7,可以明显看出经过MM-EMD方法改进后的Hilbert-Huang谱更能清晰准确地反映50 Hz信号分量出现的时间-该分量的时频分布主要集中于50 Hz附近且较少发散。仿真信号处理结果一方面表明,传统HHT方法在处理含非IMF分量的信号时存在局限-信号中的非IMF分量会降低HHT分析效果,另一方面展示了基于MM-EMD的改进HHT方法的有效性。
4.2 实测信号
运用基于MM-EMD的改进HHT方法来分析实测油压信号,一方面检验新方法的效果,另一方面将新方法应用于油压信号分析,以提取、识别油压信号中蕴含的液压系统动态特性。
该信号的时域图如图2所示。文献[2]指出,周期激励下的夹紧缸油压信号由受迫振动、自由振动、噪声等三种分量组成,并通过EMD分解、重组得到了该信号的三个分量(图3)。本节运用基于MM-EMD的改进HHT方法对该信号进行再分析。具体步骤如下:
(1)信号采样频率fs=1 000 Hz。根据文献[2]中模型计算出的自由振动频率估计值(224 Hz),取fq=400 Hz。方形结构元素长度M=fs/fq=25。
(3)对余项Xr(t)进行EMD处理,得到12个IMF分量和一个残量。

图8 液压缸油压信号的数学形态滤波结果Fig.8 The filtered result of pressure signal based on MM
(4)运用文献[2]中介绍的方法,根据各IMF分量的频率分布情况,将各IMF分量分类:c1主要为高频噪声;自由振动分量主要集中于 c2,c3,c4,c5,c6,c7 等频率分布在100~500 Hz的分量;其余分量则包含了受迫振动分量。在此基础上对信号进行重构:自由振动分量由 c2,c3,c4,c5,c6,c7 等分量叠加而成,而受迫振动分量由 c8,c9,c10,c11,c12、r等分量与广义趋势项Xq(t)叠加而成。重组可得最终结果,如图9所示。
与文献[2]中传统HHT方法相比,基于MM-EMD的改进HHT方法可以得到更好的分析效果:
(1)新方法在一定程度上抑制了模态混叠现象。对比图3(a)和图9(a)可以发现,由于模态混叠,传统EMD方法得到的高频噪声分量中出现了0.08 s左右幅度大于0.12 MPa的波动、0.2 s左右幅度大于 0.2 MPa的波动(图3(a)A、B处),基于MM-EMD的方法得到的高频噪声分量虽然也具有一定的模态混叠现象,但波动幅度都不大于0.1 MPa。
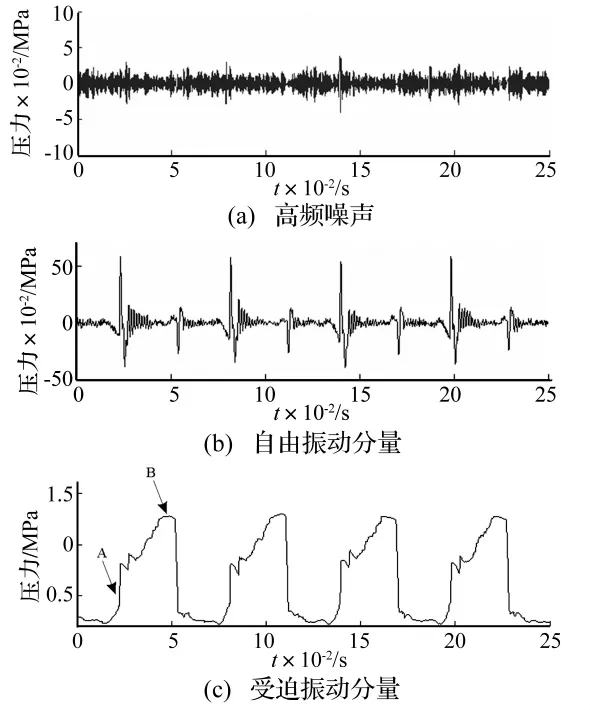
图9 夹紧缸压力信号基于MM-EMD分解重组结果Fig.9 The three components of the pressure signal based on MM-EMD
(2)新方法得到的自由振动分量与受迫振动分量体现的物理意义更为明显。图9(b)中油压基本上是以0轴为中心上下波动,而图3(b)中部分时间段(图3(b)C、E处)的油压在0轴以上波动。受迫振动分量与凸轮撞击液压缸的过程更为吻合:凸轮撞击瞬间,油压迅速上升,图9(c)中A处上升段的斜率大于图3(c)中F处的斜率,油压上升后一段时间内在1.3 MPa保持平稳,图3(c)没有这一阶段(图3(c)中H处),而图9(c)中B处较好地反映了这一过程。传统HHT方法得到的受迫振动的压力上升沿与下降沿的斜率小于原始信号(图2)的原因可能是:传统HHT方法把属于趋势项(受迫振动)的信号分量错误地分解到自由振动分量中。
以上两点表明,与传统HHT方法相比,基于MMEMD的改进HHT方法得到的自由振动分量所反映的压力波动信息更为真实可信,在处理油压信号时,新方法的分析效果更好。
5 结论
与传统HHT方法相比,基于MM-EMD的HHT改进方法增加了基于形态学的广义趋势项提取过程,虽然在一定程度上增加了信号处理的计算量,但由于形态变换的实现算法只包含布尔运算、加减法运算而不需要做乘法,因而提取过程消耗的时间较少。在相同的硬件条件下运用两种方法处理文中仿真信号时,传统方法消耗时间为3.35 s,而新方法消耗时间为4.39 s,其中广义趋势项提取过程只消耗了0.39 s,趋势项提取后的EMD与Hilbert谱分析消耗了4.00 s。虽然新方法在一定程度上增加了计算时间,但仿真与实测油压信号的处理结果表明,对于部分含有非IMF分量、非普通趋势项成分的信号,新方法能取得比传统HHT方法更好的分析效果。
[1]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proc.Roy.Soc.Lond,1998,454:903 -995.
[2]王新晴,梁 升,夏 天,等.基于HHT的液压缸动态特性分析新方法[J].振动与冲击,2011,30(7):82 -86,159.WANG Xin-qing,LIANG Sheng,XIA Tian,et al.A new method based on HHT for analyzing dynamic characteristics of a hydraulic cylinder[J].Journal of Vibration and Shock,2011,30(7):82 -86,159.
[3]Bendat J S, Piersol A G. Random data:analysis and measurement procedures[M].New York:John Wiley and Sons,1986.396-398.
[4]胡爱军.Hilbert-Huang变换在旋转机械振动信号分析中的应用研究[D].保定:华北电力大学,2008.
[5]胡爱军,唐贵基,安连锁.基于数学形态学的旋转机械振动信号降噪方法[J].机械工程学报,2006,42(4):127-130.HU Ai-jun,TANG Gui-ji,AN Lian-suo.De-noising technique for vibration signals of rotating machinery based on mathematical morphology filter[J].Chinese Journalof Mechanical Engineering,2006,42(4):127 -130.
[6]沈 路,杨富春,周晓军,等.基于改进EMD与形态滤波的齿轮故障特征提取[J].振动与冲击,2010,29(3):154-157,211.SHEN Lu,YANG Fu-chun,ZHOU Xiao-jun,et al.Gear fault feature extraction based on improved EMD and morphological filter[J].Journal of Vibration and Shock,2010,29(3):154-157,211.
[7]赵春晖.数学形态滤波器理论及其算法研究[D].哈尔滨:哈尔滨工业大学,1998.
[8]Maragos P,Schafer R W.Morphological filters-partⅠ:their set theoretic analysis and relation to linear shift invariant filters[J].IEEE Trans on ASSP,1987,35(8):1153 -1169.

