风电叶片低阶频率识别的近似解法及试验
黄雪梅,张磊安
(山东理工大学 机械工程学院,山东 淄博 255049)
风电叶片是风力发电机的关键核心部件之一,随着发电机功率的不断增大,要求叶片长度不断增加,对叶片动态响应的研究也越来越重要。模态分析作为研究叶片动态响应最常用的方法,主要是为确定叶片的第1阶、第2阶频率,可分为模态计算方法与模态试验方法[1-3]。模态计算方面,由于风电叶片形状为不规则的多自由度构件,对叶片结构的处理也比较粗糙,所以其模态参数解不易准确求得。模态试验由于该方法比较成熟、可靠,在工程上已经得到了广泛的应用。由于MW级风电叶片具有尺寸大、价格高等特点,因而现有的试验模态方法大多局限于长度不超过1 m的小叶片上[4]。吴春梅等[5]采用锤击法和正弦激励法对长度为0.6 m,额定功率为300 W的叶片进行了试验模态分析。刘旺玉等[6]对一个翼型为SG6050,半径为1 m的小型风力机叶片采用仿生学原理进行了模态试验。欧阳涛等[7-8]通过多传感器辨识和叶尖定时方法对叶片振动进行测试。
基于上述原因,本文将传递矩阵法引入到叶片的模态参数识别计算中。将叶片整体结构的力学分析问题转化为若干单元对接与传递的力学分析问题,利用矩阵相乘的计算方法实现对叶片的模态分析。引入边界条件后,确定该叶片的低阶频率计算值。最后通过构建叶片试验模态试验系统,对构件施加正弦激励,使之产生自由振动,通过安装在某些确定位置的加速度记录相应振动信号,再进行快速傅里叶变换,得到试验值,并将两者结果进行比较。
1 低频识别算法
1.1 Bernoulli-Euler Beam模型
风电叶片根部通过螺栓法兰盘被固定在筒型加载支座上,通常将其视为一个沿展向变质量的悬臂梁,主要变形为自由弯曲。目前,识别自由悬臂梁模态参数的主要方法有解析法、有限元法[9]、直接动刚度法[10-11]等。
建立风电叶片欧拉-伯努利(Bernoulli-Euler Beam)模型[12]:
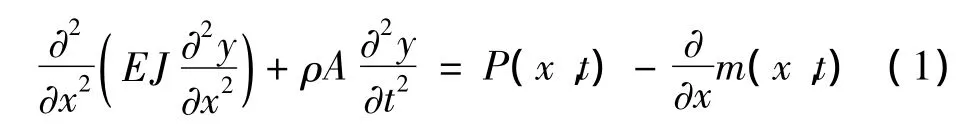
式中:y为相对于根部固定端的位移;E为叶片材料弹性模量;J为叶片截面惯性矩;ρ为叶片密度;A为横截面面积;P(x,t)为单位长度受到外力;m(x,t)为单位长度受到外力矩。
风电叶片做自由振动时,有:
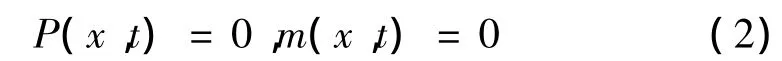
此时:
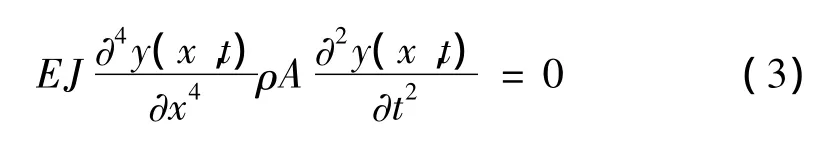
可知叶片的自由弯曲振动为四阶微分方程,由于叶片并不是真实等截面,式(3)的解析解不易准确求得,本文将传递矩阵算法应用于风电叶片的模态参数识别。
1.2 矩阵传递算法
将叶片等效成一个根部固定的变截面悬臂梁,将其分割成若干段,利用二节点梁做离散化建模,离散后模型如图1所示。图中,mi为该段的质量,li为该段长度,EiIi为该段的抗弯刚度。
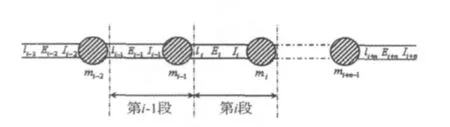
图1 二节点梁模型Fig.1 Two-node beam model
叶片做弯曲振动时,离散质量块mi除了有挠度yi和转角 θi,还有与之相对应的剪力Qi和弯矩Mi。这4个变量构成状态矢量:
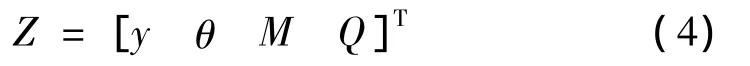
从叶片中截取第i个离散质量块,每个质量块受力分别为弯矩Mi和剪力Qi。建立其受力模型,如图2所示。
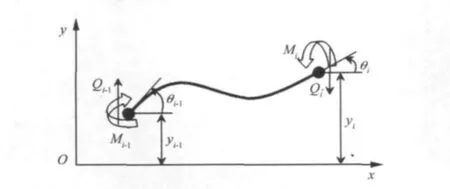
图2 二节点梁受力模型图Fig.2 Two-node beam force model picture
对叶片第i个离散质量块mi进行受力分析,左边梁li对其作用力表示为弯矩MLi和剪力QLi,右段梁 li对其作用力表示为弯矩MRi和剪力QRi。当质量块mi做简谐运动的位移为yi时,产生的惯性力可表示为miω2yi。
由于质量块两边的位移yi和转角θi相等,写成点矩阵形式,表示为:

为了建立质量块mi两边的挠度 yi和转角 θi的关系,引入材料力学关系式[13]:
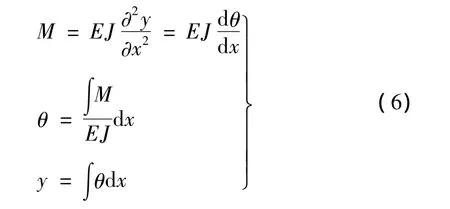
联立以上各式,建立叶片第i个质量块mi的状态矢量与第i-1个质量块mi-1的状态矢量之间关系,表示为:
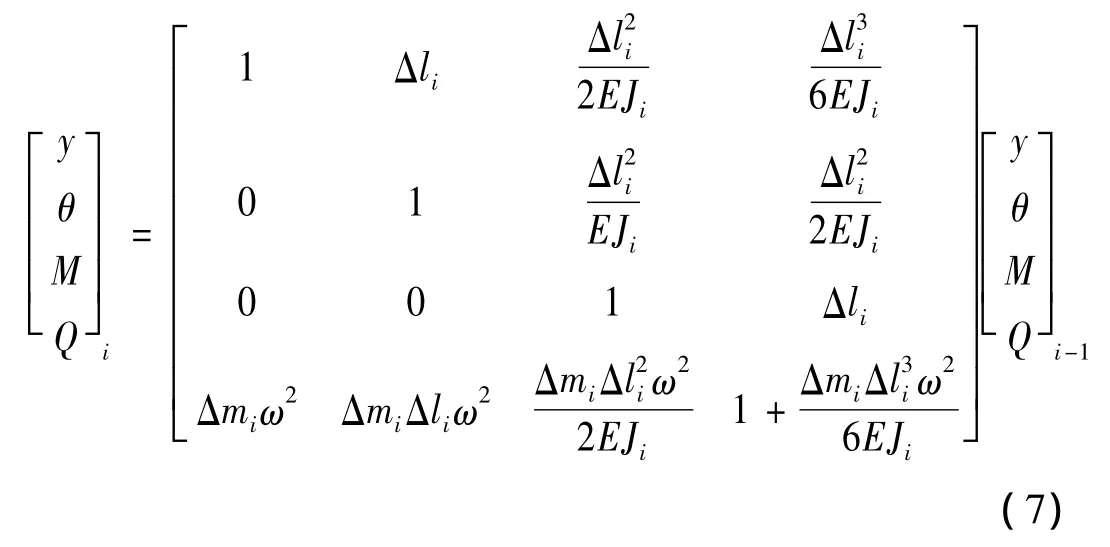
根据式(7),以 aeroblade3.6-56.4风电叶片为研究对象,沿叶片展向离散为25个元件,26个联结点。定义叶片根部为输入端,尖部为输出端,假设Pij表示第i个元件和第j个元件的联结点,每个联结点Pij对应一个状态矢量Zij。根据矩阵传递特性,每个元件的传递方程为:
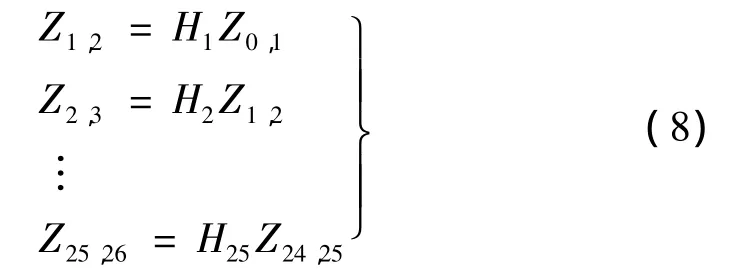
式(8)进一步表示为:

将 H25,H24…H0代入式(9),得到总传递矩阵方程:
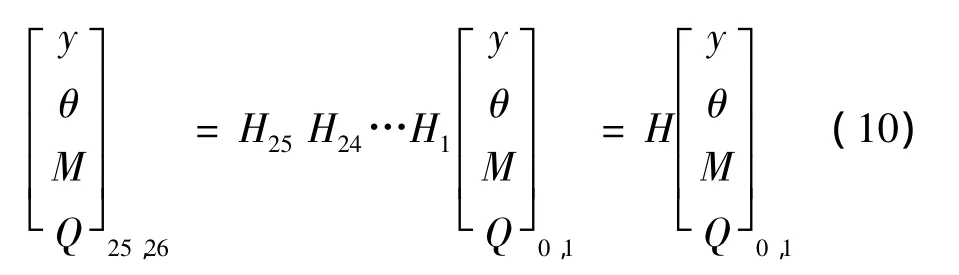
根据实际情况,边界条件分别取:
叶片根部:
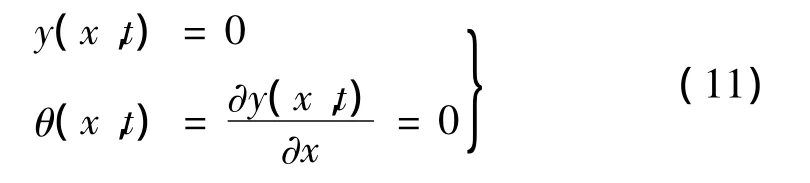
叶片尖部:
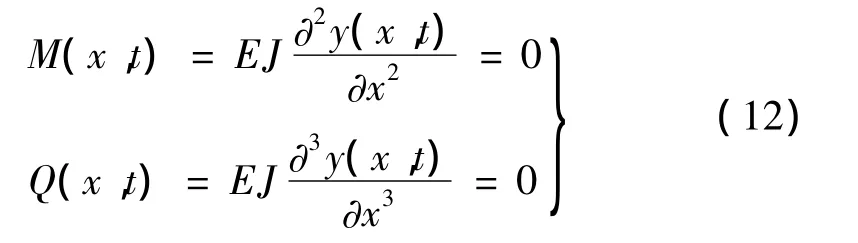
根据悬臂梁特性,将式(10)的第一行与第二行展开,得到风电叶片低阶频率识别方程,表示为:
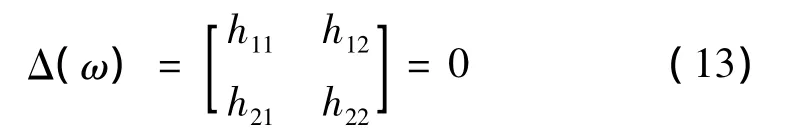
2 低频识别计算
风电叶片由截面翼型组成,叶片根部截面为圆形且较厚,中间为气动翼型,往叶尖方向逐渐变薄,主要为了满足气动性能要求。各截面翼型材料主要分为:① 叶片根部为玻璃纤维/环氧树脂;② 叶片中部为(玻璃纤维/环氧树脂)/轻木/(环氧树脂/玻璃纤维);③叶片尖部为(玻璃纤维/环氧树脂)/PVC塑料/(环氧树脂/玻璃纤维)。质量作为风电叶片的重要特征,为了保证叶片尽可能轻,内部通常采用中空构型。风电叶片的4个加载面分别定义为,最大面向(Maximum flapwise)、最小面向(Minimum flapwise)、最大弦向(Maximun edgewise)和最小弦向(Minimum edgewise)。按照结构分为:筋板-承载结构、壳体-气动结构和叶根-连接结构,总体结构如下。

图3 风电叶片截面示意图Fig.3 Wind turbine blade cross- section schematic
本文研究对象为aeroblade3.6-56.4风电叶片,其额定功率为3.6 MW,长度为56.4 m,质量为17 277 kg,重心为距离叶片根部19.05 m处。该款叶片各截面翼型主要设计参数(预弯、扭角、抗弯刚度和弹性模量等)如表1所示。
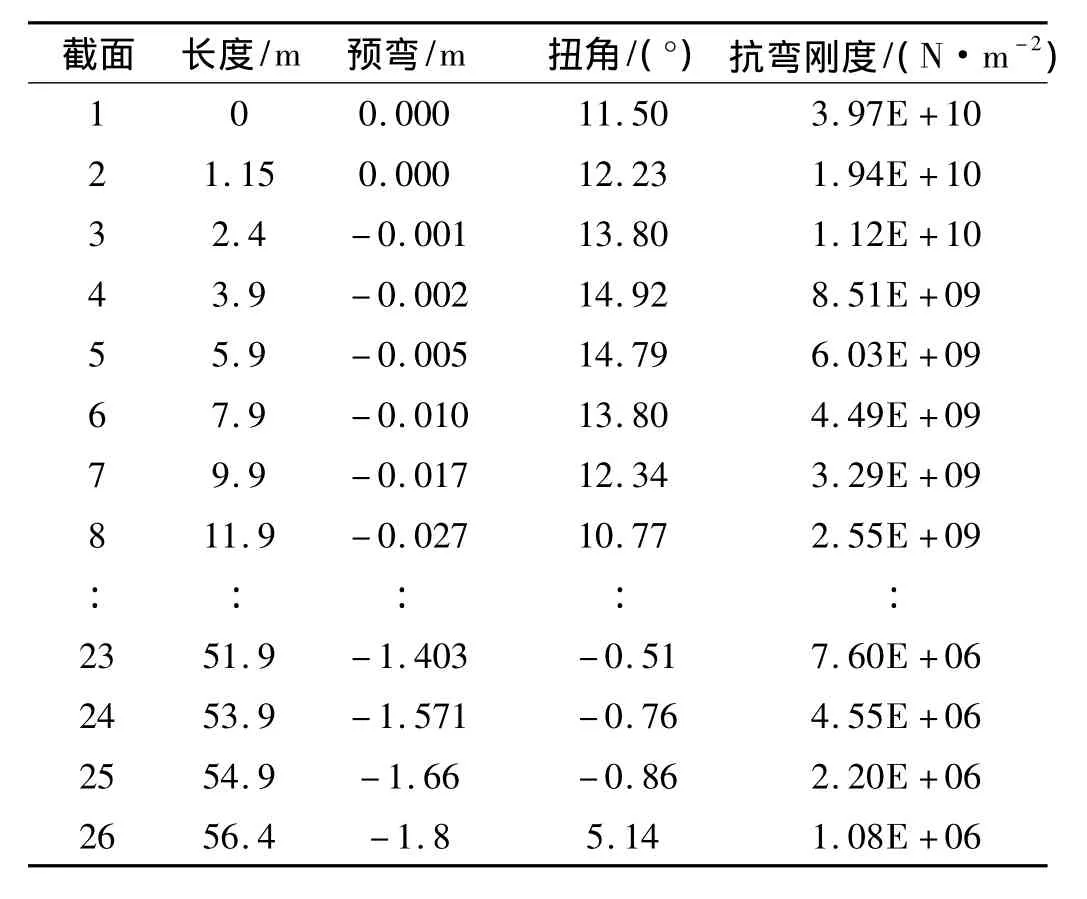
表1 叶片截面翼型设计参数Tab.1 The design parameters of each section airfoil in the blade model
根据表1中叶片各截面的设计参数,编制沿aeroblade3.6-56.4风电叶片展向的矩阵传递程序,计算出Max flapwise方向的低阶固有频率曲线,如图4所示。

图4 Aeroblade3.6-56.4风电叶片计算频率曲线Fig.4 Aeroblade3.6-56.4 wind turbine blade calculate frequency curve
从图中得出,aeroblade3.6-56.4风电叶片 Max flapwise方向的低阶固有频率计算结果分别为:一阶频率:f1st=0.68 Hz;二阶频率:f2st=1.76 Hz;三阶频率:f3st=6.46 Hz。
3 低频识别试验
为了与上述计算结果进行比较,构建一套叶片模态参数识别试验系统。
3.1 FIR滤波器设计
模态试验系统采集的原始数据中可能混有噪声,进行采样之前,需要对连续信号用低通过滤器进行滤波。基于运算精度与稳定性方面考虑,本文设计一个有限脉冲滤波器(FIR)。FIR滤波器的基本结构为一个分节的延时线,将每一节的输出值加权累加,得到滤波器的输出值。数学表示为[14-15]:
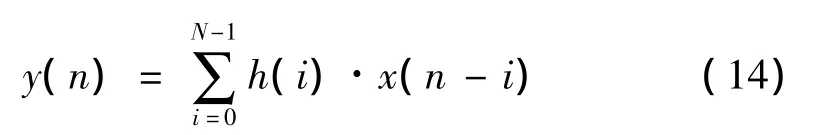
式中:N为FIR滤波器的抽头数;x(i)为第i时刻的输入样本;h(i)为FIR滤波器的第i级抽头系数。
其传递函数为:
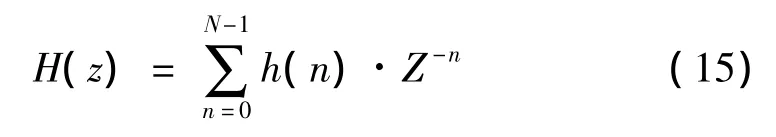
为了将傅里叶反变换导出的无限长序列变为长度为N的序列,采用矩形窗函数法进行截取。矩形窗函数表达式为:
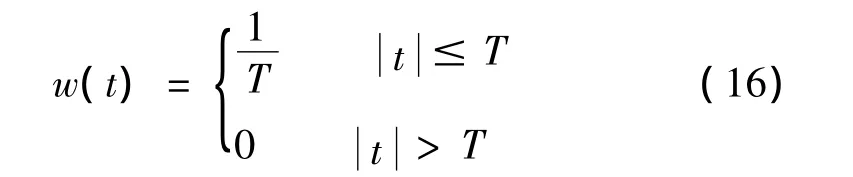
3.2 模态试验平台构建
被试验叶片目前属于国内最大的风力机发电叶片,为了对该叶片的低阶固有频率进行试验识别,构建了一个模态参数识别试验平台。筒型加载支座固定于地面,叶片根部通过88个高强度螺杆与加载支座相连,叶片处于自由悬臂状态,如图5所示。为了消除了外界因素(譬如,风载荷)影响,该试验平台布置在室内,系统的主要硬件包括加速度计、电荷放大器、数据采集仪和计算机等,主要技术指标如表2。
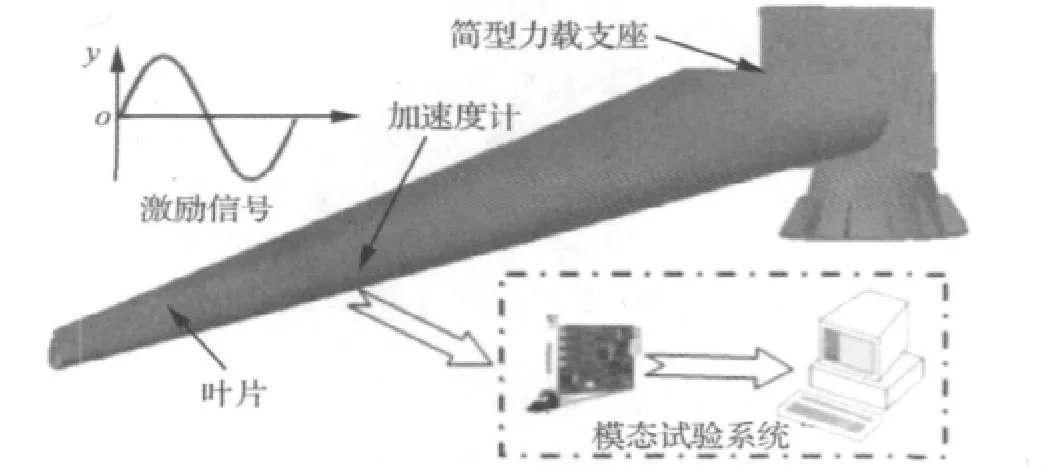
图5 模态参数识别平台Fig.5 Modal parameter identify test platform

表2 硬件设备技术指标Tab.2 The hardware device technical property
3.3 模态试验过程
将aeroblade3.6-56.4风电叶片固定在筒型加载支座上,加速度传感器置于叶片尖部,试验现场如图6所示。采用单点激励中的“不测力法”,对叶片施加一个正弦激励,引起叶片自由振动,电荷放大器将加速度信号放大并传送给信号采集装置,如图7所示。

3.4 试验结果及分析
限于篇幅,仅给出 aeroblade3.6-56.4风电叶片Max flapwise与Max edgewise方向的低阶固有频率试验结果。将数据采集仪得到的加速度信号进行FIR滤波及快速FFT变换,频谱图如图8所示。
根据图8得出,aeroblade3.6-56.4风电叶片的低阶固有频率分别为,Max flapwise1st=0.64 Hz,Max flapwise 2nd=1.68 Hz;Max edgewise1st=1.12 Hz,Max edgewise 2nd=3.64 Hz。将挥舞方向的计算结果与试验结果进行比较,两者误差不超过6%。
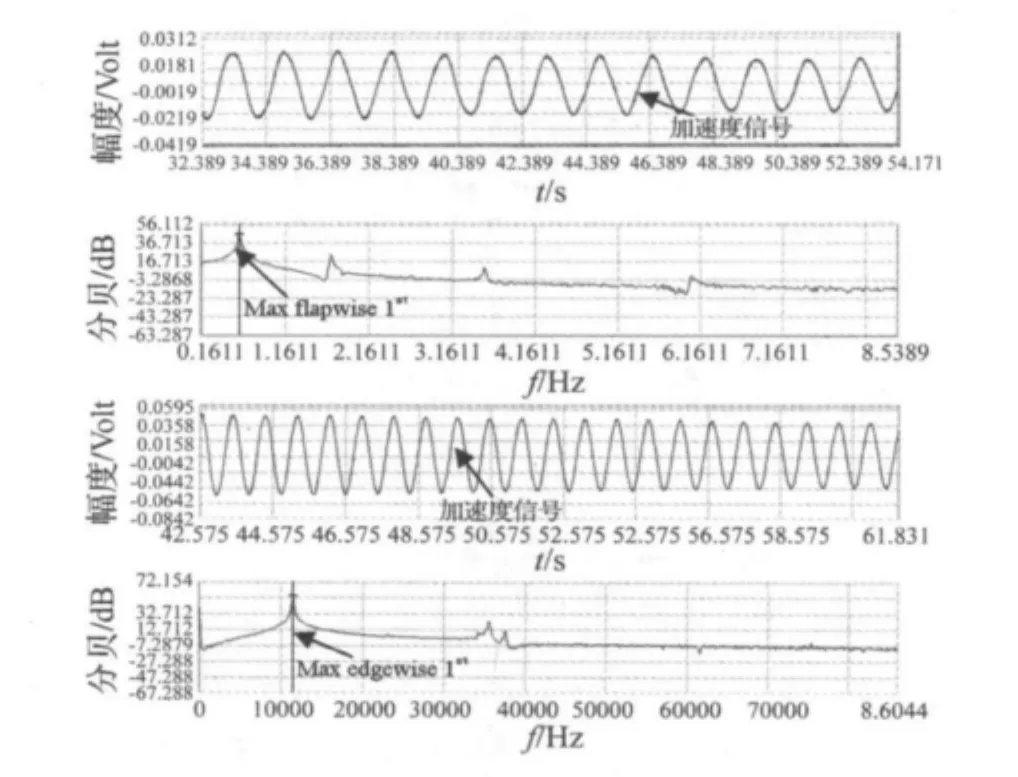
图8 aeroblade3.6-56.4风电叶片试验频率曲线Fig.8 Aeroblade3.6-56.4wind turbine blade test frequency curve
4 结论
本文将模态计算方法与试验方法相结合对风电叶片的低阶固有频率进行识别。通过将叶片沿展向离散化,建立叶片的离散化模型。编制了矩阵传递算法,将其应用于aeroblade3.6-56.4风电叶片的低阶固有频率识别计算。构建了一套大叶片模态参数识别试验平台,将模态试验结果与计算结果进行比较,两者数值基本一致,说明采用矩阵传递算法能较好地计算出叶片的低阶固有频率值,也验证了该算法的有效性。将叶片两个方向的试验结果对比,得出摆振方向的同阶固有频率远高于挥舞方向。另外,本文通过模态试验方法求出的叶片低阶固有频率,也为后续的风电叶片疲劳加载系统研发及试验奠定了基础。
[1] 毛火军,石可重,李宏利,等.大型风电叶片的模态测试与数值模拟[J].工程热物理学报,2009,30(4):601-604.MAO Huo-jun,SHI Ke-chong,LI Hong-li,et al.Modal testing and numerical simulation of large wind turbine blade[J].Journal of Engineering Thermophysics,2009,30(4):601-604.
[2] Cha P D,de Pillis L G.Model updating by adding known masses[J].International Journal for Numerical Method in Engineering,2001,50:2547-3571.
[3] Ryu J,Kim Sang,Kim Sung Soo.Ageneral approach to stress stiffening effents on flexible multibody dynamic systems[J].Mech Struct&Mach,1994,22(2):157-180.
[4] 叶枝全,马昊旻,丁 康,等.水平轴风力机桨叶的实验模态分析[J].太阳能学报,2001,22(4):473-476.YE Zhi-quan,MA Hao-min,DING Kang,et al.Experimental model ananlysis of the rotor blade of the horizontal axis wind turbine[J].Acta Energiae Solaris Sinica,2001,22(4):473-476.
[5] 吴春梅,田 瑞,刘 博,等.小型水平轴风力机叶片的振动研究[J].能源技术,2006,27(5):205-207.WU Chun-mei,TIAN Rui,LIU Bo,et al.Study on small size blade vibration characteristic of the horizontal axis wind turbine[J].Energy Technology,2006,27(5):205-207.
[6] 刘旺玉,张海全,李明刚.基于仿生设计的风力发电机叶片力学性能的实验研究[J].实验力学,2009,24(2):121-125.LIU Wang-yu,ZHANG Hai-qian,LI Ming-gang.Experimental study of mechanical performance of wind turbine blade based on bionic design[J].Journal of Experimental Mechanics,2009,24(2):121-125.
[7] 李孟麟,段发阶,欧阳涛,等.基于叶尖定时的旋转机械叶片振动频率识别 ESPRIT方法[J].振动与冲击,2010,29(12):18-21.LI Meng-lin,DUAN Fa-jie,OUYANG Tao,et al.ESPRIT Method for blade vibration frequency identification in rotating machinery based on blade tip-timing measurement[J].Journal of Vibration and Shock,2010,29(12):18-21.
[8] 欧阳涛,郭文力,段发阶,等.基于叶尖定时的旋转叶片同步振动辨识新方法[J].振动与冲击,2011,30(8):247-252.OUYANG Tao,GUO Wen-li,DUAN Fa-jie,et al.New method for identifying rotating blades synchronous vibration based on tip-timing[J].Journal of Vibration and Shock,2011,30(8):247-252.
[9] Martinerz C A E,Museros P,Castillo L A.Semranalytic solution in the time domain for non-uniform multispan Bernoulli- Euler beams traversed by moving loads[J].Sound Vib,2006,294(1):277-278.
[10] Henchi K,Fafard M.Dynamic behaviour of mulitispan beams under moving loads[J].Sound Vib,1997,199(1):33-35.
[11] Dugush Y A,Eisenberger M.Vibrations of nonuniform continuous beams under moving loads[J].Sound Vib,2002,254(5):9-11.
[12] 王光远.建筑结构的振动[M].北京:科学出版社,1978.
[13] 贺兴书.机械振动学[M].上海:上海交通大学出版社,1985.
[14] 彭红平,杨福宝.基于Matlab的FIR数字滤波器设计[J].武汉理工大学学报(信息与管理工程版),2005,27(5):275-278.PENG Hong-ping,YANG Fu-bao.Design of FIR digital filter based on matlab[J].Journal of WUT(Information & Managementent Engin-eering),2005,27(5):275-278.
[15] 李 辉,张 安,赵 敏,等.粒子群优化算法在FIR数字滤波器设计中的应用[J].电子学报,2005,33(7):1338-1341.LI Hui,ZHANG An,ZHAO Min,et al.Particle swarm optimization algorithm for FIR digital filters design[J].Acta Electronica Sinca,2005,33(7):1338-1341.

