断口定量分析在直升机关键动部件疲劳试验分析中的应用
王胜霞,窦松柏
(中国直升机设计研究所,江西景德镇 333001)
0 引言
疲劳断裂是直升机关键动部件试验过程中断裂的主要破坏模式。据有关资料统计,由于结构部件失效导致的重大事故中,80% ~90%与疲劳断裂有关[1],而动部件的疲劳寿命由裂纹萌生寿命和裂纹扩展寿命构成,由断裂力学的观点可知,金属结构件的疲劳破坏是由于主裂纹扩展到临界尺寸而造成的,而构件的寿命取决于结构设计薄弱且应力较大部位裂纹的萌生和扩展。对于服役机型,通过断口定量分析,可以反推出实际工作中的疲劳裂纹的扩展寿命,进而反推裂纹的萌生寿命;对于直升机研制过程中的疲劳试验,可以对断口上源区形成的先后顺序进行反推,为疲劳强度分析提供准确的依据。断口定量分析有利于正确分析事故的原因,解决工程试验中的实际问题。
1 断口定量反推的理论基础
疲劳断裂过程分为疲劳裂纹的萌生、扩展和失稳断裂三个阶段。由于国内目前尚未有数学物理模型对疲劳裂纹的萌生阶段进行反推,国内外的专家学者将扩展阶段的数学物理模型定量表征视为疲劳断裂研究的重点领域。短裂纹形成后的裂纹扩展是一个连续过程,与循环载荷有关,在载荷循环的过程中,裂纹扩展形成一条疲劳条带,即当疲劳裂纹长度为a时,一次疲劳载荷循环dN使疲劳裂纹扩展da的距离[2]。对于大多数结构材料,在裂纹的扩展阶段,通过扫描电镜、投射电镜可以看到清晰的疲劳条带,并且随着裂纹长度的增加,疲劳条带间距呈逐渐加宽的趋势[3]。断口的定量反推主要是针对疲劳裂纹扩展阶段进行量化测量与计算。
目前常用的定量分析物理数学模型主要有Paris公式、梯形法、断口宏观特征模型等。
1.1 Paris公式
利用断口反推计算疲劳裂纹扩展寿命的依据是选用合适的疲劳裂纹扩展速率da/dN的数学表达式。有关描述疲劳裂纹扩展速率da/dN的数学表达式很多,但最为适用且应用广泛的表达式是人们熟知的Paris公式。
对于一般金属材料在疲劳稳定扩展区的裂纹扩展,Paris公式指出其裂纹扩展速率和裂纹长度之间有如下关系:
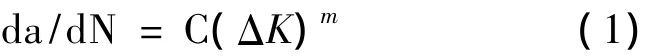
式中:C,m 为材料常数,ΔK=Δσ(πα)1/2Y(a,b),Y为与裂纹有关的构件形状因子,Δσ为最大应力σmax和最小应力σmin之差,a为裂纹长度。
在第二扩展阶段的一定范围内,裂纹微观扩展速率即疲劳条带宽度等于裂纹宏观扩展速率,条带宽度代表断口上该处的疲劳裂纹扩展速率[3]。
对裂纹扩展速率随裂纹长度呈有规律增加的情况,可对裂纹长度和裂纹的扩展速率分别取常用对数或自然对数,然后用取对数之后的数据进行拟合,如果对数之后的数值点有规律地分布在拟合曲线(直线)的两侧,则说明裂纹的扩展情况能较好地符合paris公式。对Paris公式进行一系列的设定和变
换,则可以得到表达疲劳扩展寿命的表达式:
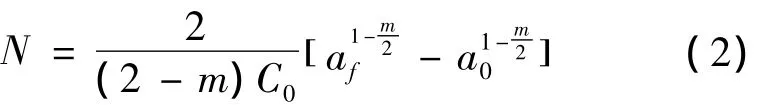
常数c0和m可由如下方法确定:即对(2)式取对数得到(3)式。
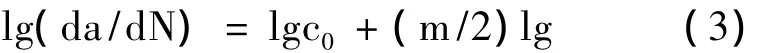
则lg(da/dN)与lga为直线,即裂纹扩展速率da/dN与裂纹长度在双对数坐标下有直线关系,并且截距为lgc0,斜率为m/2。
对于不同裂纹长度ai所对应的(da/dN)i,则可按(3)式进行拟合或分段拟合,求出c0和m值,并确定af和a0的值代入(2)式,即可求出疲劳扩展寿命[3]。
1.2 梯形法
梯形法是基于微分的原理,将疲劳寿命分成很小的小段然后累积起来[4],其表达式见公式(4):

式中:an为第n点距离源区的裂纹长度,an-1为第n-1点距离源区的裂纹长度;dNn为第n点处裂纹扩展速率的倒数,dNn-1为第n-1点裂纹扩展速率的倒数。
运用梯形法进行定量计算时,如果所选用的a0值(裂纹开始扩展时的尺寸)比离源区最近可测量疲劳条带间距的位置距源区的距离a1小,则这时a0没有疲劳条带宽度值。据有关资料[3]研究表明,直接利用梯形法计算a0到a1小段上的疲劳扩展寿命时,是认为a0处的扩展寿命为零,这样会人为将该小段上的疲劳扩展寿命变小。由于靠近源区的疲劳条带间距较小,忽略其倒数会引起较大的误差。因此,当a0大于a1或二者非常接近时,可直接套用梯形法公式;当a0小于a1时,应用梯形法计算疲劳扩展寿命需对梯形法进行修正,具体修正方法:在利用梯形法公式计算a0值到a1(第一个测量点)之间的寿命时,公式(4)不除2,第一个测量点值后的算法保持不变[3]。工程上往往取 a0值为0.3 ~0.5[2]。
据资料研究,Paris公式适合于实验室简单实验载荷条件下且试样结构简单的断口定量分析,而梯形法则适用于结构复杂且载荷为非恒幅条件下的定量反推。在实际的工程应用条件下,载荷往往为非横幅疲劳载荷,存在裂纹扩展速率呈无规律分布的情况,这种条件下用Paris公式进行疲劳寿命定量分析就很繁琐,引入很大的误差。因此对复杂结构件且非恒幅载荷条件下的零部件往往采用列表梯形法进行疲劳寿命定量分析。
2 断口反推在直升机关键动部件疲劳试验分析中的应用
直升机某构件支臂进行高周疲劳试验,循环80万次后在异型螺母安装孔处断裂,将断口分为A、B两部分。异性螺母安装孔处主要的受力为离心力、挥舞弯矩。
从断口观察可知,A断口宏观下断口形貌(如图1)源区起源于紧固螺栓安装孔的一边磨损区域,呈小线源起始。从扩展区宏观形貌来看,扩展区外观形貌细密,呈圆弧状向另一边扩展,且扩展区部分面积颜色较暗,边缘处有磨擦痕迹;瞬断区与扩展区有一定的角度,高差较大,形貌较粗糙。

图1 A断口整体形貌
对B断口进行观察(如图2),源区从异型螺母安装孔的倒角处起始,呈小线源,源区周围区域呈金属光泽,无腐蚀特征,断口源区起始处磨损轻微;扩展区形貌平坦,面积约占整个面积的一半,整个断口较A断口新鲜,扩展区外观形貌较A断口粗糙;瞬断区形貌也较平整,断面较粗糙,边缘有剪切唇。
根据上述宏观颜色、形貌、磨损程度等方面的观察分析认为,A断口首先萌生裂纹并扩展,扩展一定时间后,B断口开始萌生裂纹并扩展。为了验证断口分析的正确性,利用定量分析的方法对断口进行疲劳寿命反推。
在扫描电镜下对疲劳A断口和B断口从源区进行观察,测得裂纹临界长度,然后沿着主裂纹扩展方向,依次测量疲劳条带的平均间距,然后计算出疲劳循环次数,结果见表1和表2。从A、B断口裂纹扩展长度与扩展速率关系图(图3和图5)看,裂纹扩展速率并不是随着裂纹长度的增加而增加,而是无规律增大或减小。而裂纹循环次数则是随着裂纹扩展长度的增加而增加(如图4和图6)。

图2 B断口整体形貌
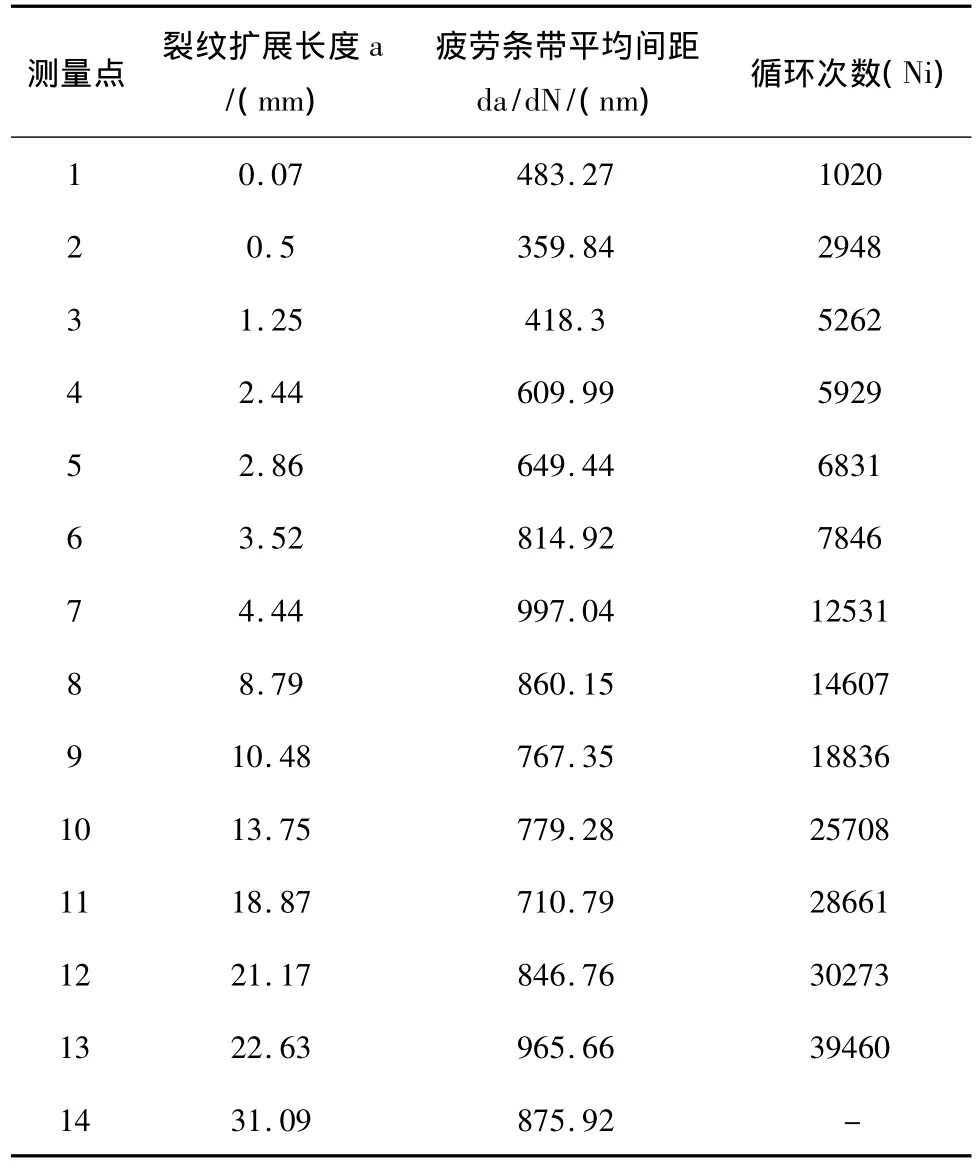
表1 A断口裂纹扩展速率相关数据
A断口中ac小于工程上常应用的值0.5mm,利用梯形法计算不需要进行修正[3]。测量的数据用梯形法经过计算,A断口疲劳裂纹从a0扩展至临界裂纹ac的循环次数Np为:Np=39460(次)。因此,该疲劳裂纹从萌生寿命循环次数Ni为:
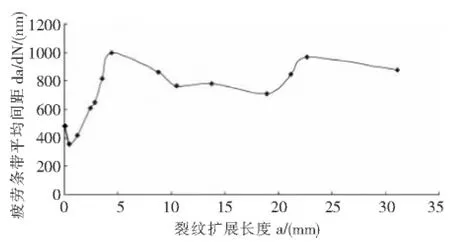
图3 A断口裂纹扩展长度与裂纹扩展速率关系
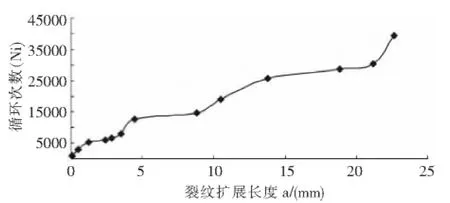
图4 A断口裂纹扩展长度与循环次数关系
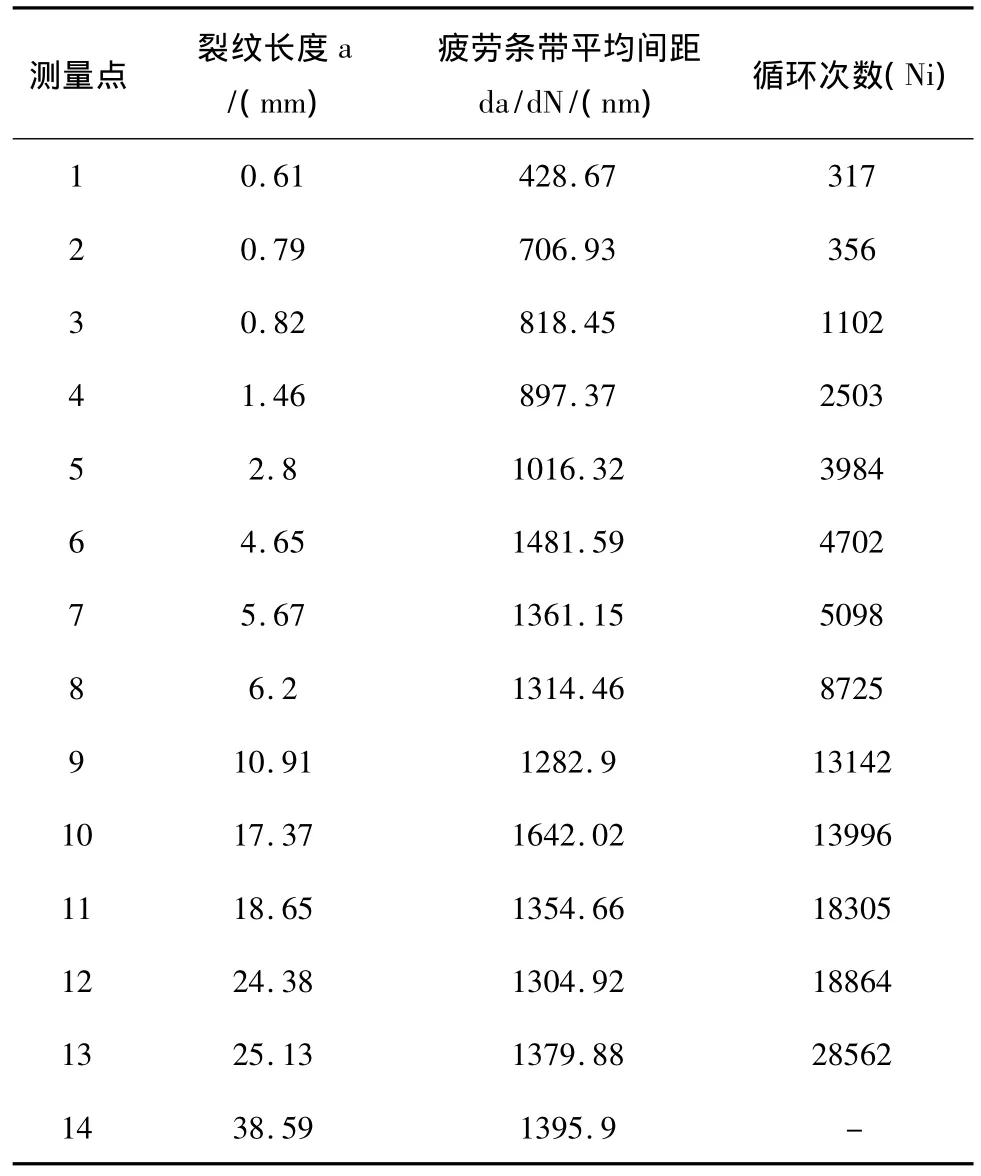
表2 B断口裂纹扩展速率相关数据

而B断口中ac大于0.5mm,要用梯形法进行修正,修正后推得B断口疲劳裂纹从a0扩展至临界裂纹ac的循环次数Np为:Np=28562(次)。因此B断口的疲劳裂纹的萌生寿命循环次数Ni为:
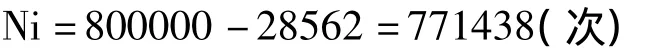
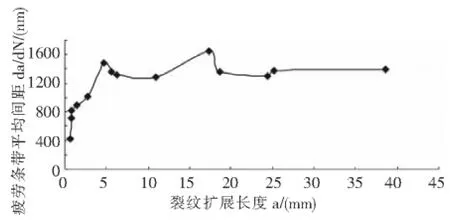
图5 B断口裂纹扩展长度与裂纹扩展速率关系

图6 B断口裂纹扩展长度与循环次数关系
从上述试验数据可推断,A断口的萌生寿命比B断口的萌生寿命短,因此零部件A处首先开裂。国内外许多专家对断口定量反推进行了多方面的研究,但应用定量分析对疲劳断口进行首断件判定的研究较少。本文主要通过同一零部件上的两个断口,考察定量分析在断口首断件判定应用的可行性,试验数据结果表明可以通过定量分析判定首断件。但由于目前试验件断口形貌的限制,且裂纹扩展方向的选择和扫描电镜测量疲劳条带区域的选择都带有随机性,因此仪器、条带测量、选择的裂纹扩展方向等都在一定的程度上会带入误差。
3 结束语
断口是一个零部件断裂过程中源区、扩展区、瞬断区的真实记录,记录了材料在载荷和环境作用下裂纹萌生、扩展至断裂的全过程。通过断口定量分析可以反推其疲劳扩展寿命,进而可推测出裂纹的萌生寿命,它在失效原因分析、结构件首断件的判定、零部件检修周期的确定等方面具有重要的作用。
根据实际工程试验观察,梯形法比Paris公式更适用于工程试验的定量分析,Paris公式用于工程试验过于复杂[5]。运用梯形法进行定量反推实例分析,结果表明应用断口定量分析判定首断件在工程应用中是可行的。后续的研究和分析工作更应该注重于减少定量分析的误差,力求接近真实数据。
[1]章文峰,闫海.断口定量分析在评估构件疲劳寿命中的应用[J].材料工程,2000(4):45-48.
[2]张 栋,钟培道,陶春虎.机械失效的实用分析[M].北京:国防工业出版社,1997:111-401.
[3]刘新灵,张卫方,陶春虎.不同断口定量分析疲劳寿命模型应用对比[J].机械工程材料,2008(5):4-6.
[4]张 栋.桨叶大梁疲劳破坏分析和疲劳周次的定量计算[J].直升机技术,1983(4):1-9.
[5]陶春虎,习年生,张卫方,等.断口反推疲劳应力的新进展[J].航空材料学报,2000,20:162.

