基于滑移网格的临近空间螺旋桨流场数值仿真

程钰锋，聂万胜，胡永平

(1.装备学院研究生院，北京怀柔 101416;2.装备学院航天装备系，北京怀柔 101416;3.河北沧州飞行训练基地，河北沧州 061036)

0 引言

现今油价大幅上涨，节油成为飞行器设计中必须考虑的一个环节［1］。螺旋桨发动机因其在亚音速范围内的节油优点引起了人们的普遍关注和高度重视，螺旋桨的研究工作也得到了进一步的发展。螺旋桨气动性能的研究是螺旋桨动力系统研制工作的关键，国内外许多专家学者都采用计算流体力学(computational fluid dynamics，CFD)技术研究了螺旋桨的气动性能，取得了很多有意义的成果。CFD是近三十年来迅速发展的技术，但它已经广泛的渗入到社会和生活的各个方面，在研究流动现象、解决流体工程问题等方面发挥了重要作用，尤其在航空航天领域已成为不可或缺的核心技术之一［2］。

螺旋桨和旋翼流场的复杂性使得螺旋桨、旋翼CFD技术总体落后于固定翼CFD技术［3］。起初，人们采用小扰动势方程法［4］研究螺旋桨的旋转流场，但由于使用了小扰动的假设，只对于薄翼等扰动不太强的跨音速流动才能给出较好的结果。后来，有人采用全势方程法［5-7］研究螺旋桨的旋转流场，全势方程求解的复杂程度介于欧拉方程和小扰动方程之间，在激度不太强的情况下，具有较好的模拟精度。为了更准确地模拟旋翼流场中出现的激波和旋涡流动，从20世纪80年代以来，许多研究以欧拉方程和N-S方程来求解旋翼流场［8］。我国的研究工作始于20世纪90年代。1993年，西北工业大学的杨国伟和何植岱［9］采用涡格升力面法，建立一种三维自由尾涡模型，构造一种松弛迭代法，计算得到了收缩尾涡。1996年，西北工业大学的王立群、乔志德等人［10-11］，采用网格中心有限体积法和五步Ruuge-Kutta(5，2)时间推进格式，通过求解三维欧拉方程，仿真得到了直升机旋翼悬停流场，在没有任何尾迹模型的情况下，计算了两旋翼在亚声速和跨声速时的压力分布。1998年，上海交通大学的杜朝晖［12-13］为解决水平轴风力涡轮设计与性能预估方法存在失速延迟现象的问题，以旋转叶轮三维边界层方程为理论基础，在分析了风力涡轮叶片表面产生失速延迟的机理后，建立了风力涡轮设计与评估方法的三维失速延迟修正模型，提高了水平轴风力涡轮的设计水平。20世纪初，国内关于螺旋桨气动仿真的研究较少。2008年，中科院的聂营、王生等人［14-15］采用Gambit软件对螺旋桨进行几何建模，再用Fluent软件基于滑移网格，仿真研究了临近空间螺旋桨的气动性能。2008年，西工大的许建华、宋文萍等人［16］采用雷诺平均N-S方程和嵌套网格技术对美国国家可再生能源实验室的CER实验型风力机叶片进行了仿真研究，湍流方程是B-L代数模型;计算中采用了有限体积空间离散法和改进型隐式LU-SGS时间推进格式，所用的嵌套网格技术有效的捕捉了螺旋桨的尾涡;在此基础上，2009年［17］，他们采用在不同粗细网格上消除不同频率误差加速解的收敛的多重网格技术，仿真研究了螺旋桨侧流粘性流场，其中多重网格采用非线性方程的全近似格式(FAS)。2010年，西工大的罗淞、杨永等人［18］采用多块点对点网格生成技术，生成了螺旋桨的空间计算网格，分别研究了欧拉方程组和N-S方程组对不同进距比下螺旋桨运动过程的仿真结果，与实验进行对比后得出欧拉方程比较适合于螺旋桨的工程设计。

临近空间低速飞行器大多采用螺旋桨作为其动力装置，螺旋桨气动性能的优劣决定临近空间低速飞行器的性能，因此，研究临近空间环境下螺旋桨的气动性能是十分迫切的工作，但临近空间环境特殊，很难开展实验研究［19］。基于此，本文采用滑移网格模型，考虑RNG k-ε湍流模型，通过求解三维非定常N-S方程，在验证了数学模型可行性的基础上，仿真研究了临近空间螺旋桨非定常旋转流场。仿真结果与文献资料和理论分析一致，可以用于临近空间螺旋桨的设计和研究。

1 数学模型

1.1 控制方程

对于N-S方程，连续方程、动力方程和能量方程的通用形式可以写成如下形式。

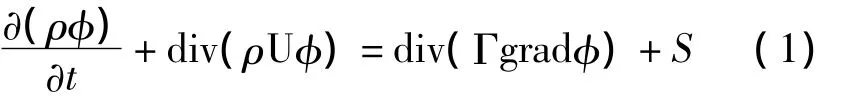
其中:ρ是气体密度，U是速度矢量，φ是通用变量，Γ是广义扩散系数，S是广义源项。对于连续方程、动力方程和能量方程，φ分别为1、ui和T;Γ分别为0、μ 和 k/cp;S分别为0、-∂p/∂xi和 ST。ui是速度分量，T是温度，μ是粘性，k是流体的传热系数，cp是比热容，ST是粘性耗散项，即流体的内热源及由于粘性作用流体机械能转换为热能的部分。

理想气体状态方程为:

式中R是气体常数。

1.2 湍流模型

RNG k-ε湍流模型是基于k-ε标准两方程的湍流模型，采用一种叫做重正规化群的数学方法对N-S方程进行暂态推理得到的改进型k-ε两方程湍流模型。它由V.Yakhot和S.A.Orszag于1986年提出并逐步完善的［20-21］，其基本思想是认为在流场中小涡是各项同性的，处于统计定常的和统计平衡的状态。忽略浮力湍动能的RNG k-ε湍流模型的输运方程如下:

其中:k是湍流动能，ε是湍流耗散率;ui是速度分量，xi是坐标分量;αk=αε=1.393 分别是 Prandtl数对k和ε的反馈作用系数;ueff是有效粘性系数，Gk是由平均速度梯度引起的湍动能;YM是由于可压缩湍流脉动膨胀对总的耗散率的影响;C1ε=1.42、C2ε=1.68是经验常数;Rε是湍流模型中数的解析项。

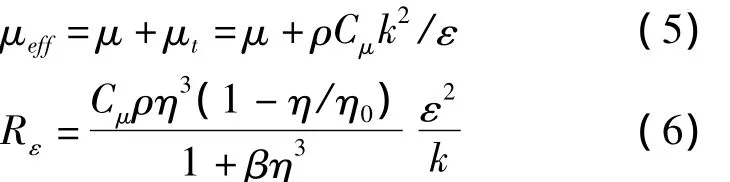
式中:Cμ=0.0845;η0=4.38;β =0.012;η =Sk/ε，S是漩涡大小。

由上可知，RNG k-ε湍流模型考虑了低雷诺数流动粘性，改进了标准k-ε模型的高雷诺数性质，并且提供了Prandtl数的解析公式，考虑了湍流漩涡，因此更加适合于雷诺数不是很高和带有强漩涡运动状态的数值仿真。

1.3 计算方法

采用耦合求解器，首先同时求解连续方程、动力方程和能量方程，然后求解湍流方程。耦合算法的流程比较简单，如图1所示。在耦合算法中使用隐式格式，即通过求解方程组的形式求解流场变量，它是使用块 Gauss-Seidel法与 AMG法(Algebraic Multi-Grid，代数多重网格法)联合完成的。

采用二阶精度的有限体积AUSM(Advection Upstream Splitting Method)离散格式对粘性流体的控制方程和湍流方程进行空间离散。AUSM格式是20世纪90年代Liou和Stefen提出并完善的高分辨率迎风格式，融合了FVS稳定性好的优点和FDS高分辨率的优点，具有良好的数值稳定性和较高的间断分辨率，其基本思想是认为对流波的传播与声波的传播是物理上不同的过程，前者与特征速度u为线性关系，后者与特征速度u+a和u-a有非线性关系，将无粘通量分解为对流通量和压力通量。详见文献［22］。

图1 耦合算法流程图

1.4 滑移网格模型

滑移网格是在动参考系模型和混合面法的基础上发展起来的，常用于风车、转子、螺旋桨等运动的仿真研究。在滑动网格模型计算中，流场中至少存在两个网格区域，每一个区域都必须有一个网格界面与其他区域连接在一起。网格区域之间沿界面做相对运动。在选取网格界面时，必须保证界面两侧都是流体区域。

滑动网格模型允许相邻网格间发生相对运动，而且网格界面上的节点无需对齐，即网格交界面是非正则的。在使用滑动网格模型时，计算网格界面上的通量需要考虑到相邻网格间的相对运动，以及由运动形成的重叠区域的变化过程。

两个网格界面相互重合部分形成的区域称为内部区域，即两侧均为流体的区域，而不重合的部分则称为“壁面”区域(如果流场是周期性流场，则不重合的部分则称为周期区域)。在实际计算过程中，每迭代一次就需要重新确定一次网格界面的重叠区域，流场变量穿过界面的通量是用内部区域计算的，而不是用交界面上的网格计算。

下面，通过一个简单的例子说明滑移网格是如何计算界面信息的。图4是二维网格分界面示意图，界面区域由面A-B、B-C、D-E和面E-F构成。交界区域可以分为a-d、d-b、b-e等。处于两个区域重合部分的面为d-b、b-e和e-c，构成内部区域，其他的面(a-d、c-f)则为成对的壁面区域。如果要计算穿过区域IV的流量，用面d-b和面b-e代替面D-E，并分别计算从I和III流入IV的流量。

图2 二维网格分界面示意图

1.5 模型验证

［15］，通过比较螺旋桨的静拉力，验证上述数学模型的可行性。螺旋桨的几何建模及网格划分在gambit环境下完成，直径为28 in，螺距为10 in，具体尺寸详见文献［15］。

表1是文献［15］的实验和计算结果与本文计算结果的比较。由表1可见，文献［15］的计算结果与实验结果的最大误差为20%，本文计算结果与实验数据的最大误差为15.8%，本文计算结果与实验数据更为接近，说明本文所用计算模型是可行的。

表1 静拉力的比较

2 螺旋桨模型及网格

图3是本文所研究的螺旋桨局部及其网格示意图，螺旋桨叶素选择Eppler 387翼型，不同桨径处的叶素弦长和安装角都相同且分别为0.05m和20°，螺旋桨直径D为0.8 m，两个桨叶之间的轮毂是长0.06 m、直径0.03 m的圆柱体。计算区域是一个长10 D、直径8D的圆柱体。速度入口距螺旋桨4D，给定气流速度及总温，压力出口距螺旋桨6D，给定总温和总压;远场距螺旋桨转轴4D，给定气流速度、总压及总温，如图4所示。

由于滑移网格模型允许相邻网格之间发生相对运动，而且网格界面上的点无需对齐，即网格是非正则的。利用这一特点，可以更好的分布网格的疏密度，既保证了计算流场所需要网格数又使网格总数减小，从而节约计算资源。对螺旋桨的仿真而言，螺旋桨近区域流场变化剧烈，所以应该加密网格，远离螺旋桨的区域流场较为平缓，对网格数目要求不高，所以网格数目较少。

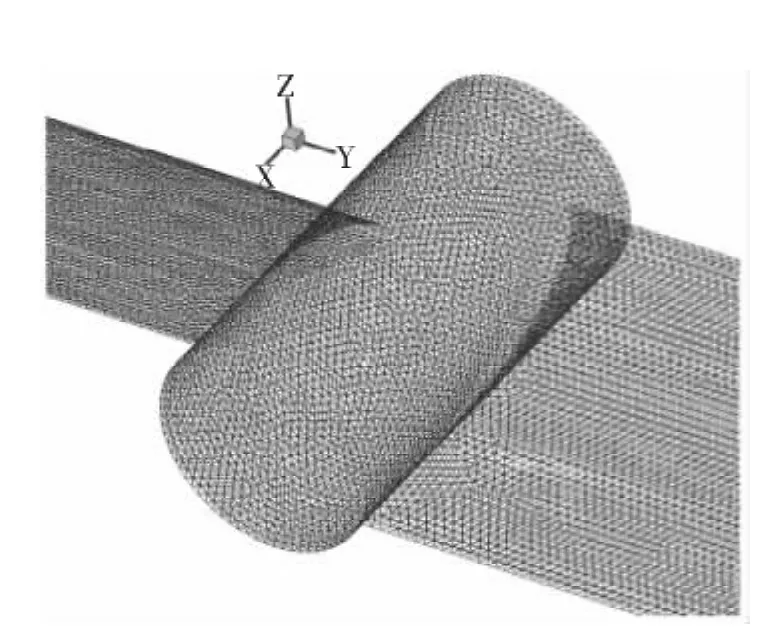
图3 螺旋桨局部网格示意图

图4 计算区域及网格示意图

图4是整个计算区域的网格示意图。整个计算区域共分为3个小区域。旋转区域是中间包围螺旋桨的一个小区域，该区域网格为非结构网格，网格数约为60万。旋转区前后的两个区域网格为结构网格，网格数约为12万。

对螺旋桨的仿真而言，螺旋桨近区域流场变化剧烈，所以应该加密网格，远离螺旋桨的区域流场较为平缓，对网格数目要求不高，所以网格数目较少。基于此，本文将计算区域分为气流入口区域、旋转区域和气流出口区域3个小的计算区域。螺旋桨前后的气流入口和出口区域采用TTM［23］方法生成结构网格，并在各自靠近螺旋桨的一端加密，网格总数约为12万。旋转区域采用TGrid网格划分法生成非结构网格，螺旋桨表面网格节点之间距离为1 mm，网格总数约为60万。

3 仿真结果及分析

本节在飞行高度为20 km，螺旋桨前进速度分别为5 m/s和20 m/s的条件下，对不同转速下螺旋桨的运动过程进行仿真，分析螺旋桨拉力、效率随转速的变化规律及其原因，研究螺旋桨速度、涡流强度等参数在旋转流场中的分布规律。

图5是前进速度为5 m/s和20 m/s时，螺旋桨的拉力和效率随其转速的变化规律比较图。其中螺旋桨的效率η=TV0/2pinsM，T是螺旋桨总拉力，M是总扭矩，ns是转速，V0是螺旋桨的前进速度。由图可见，当螺旋桨的前进速度不相同时，螺旋桨的气动性能随转速变化而变化的规律相同，但总的气动性能如拉力系数和效率还是有所差别，前进速度为20 m/s时拉力和效率比前进速度为5 m/s时稍大。由图5(a)可见，在同一个前进速度条件下，螺旋桨拉力随转速的减小而减小;当转速减小到一定的程度后，螺旋桨拉力变为负值，这是因为螺旋桨的工作状态已经由前进状态转为制动状态，此时螺旋桨不产生拉力，而产生与飞行方向相反的阻力。由图5(b)可见，螺旋桨的气动效率随转速的增大先增大后减小，与文献［19］的分析结果一致。

图5 `拉力和效率随进距比的变化

图6是前进速度为5 m/s，转速分别为60 rpm、180 rpm和1200 rpm时部分叶素周围压力系数分布比较图，其中压力系数Cp=2(p-p0)/ρV02，p 是流场压力，p0是环境压力。

图6 前进速度为5 m/s时叶素拉力系数分布比较图

由图6(a)可见，当前进速度为5 m/s，转速为60 rpm时，叶素吸力面压力系数大于升力面压力系数，即桨叶迎风面的压力系数大于背风面压力系数，说明该工况下桨叶产生与飞行方向相反的阻力，螺旋桨处于制动状态。但压力面和升力面的压力系数差别不是很大，因此此时所产生的负拉力比较小，与图5(a)所示一致。

由图6(b)可见，当转速增大到180 rpm时，螺旋桨的工作状态已经由制动状态转向了前进状态，叶素吸力面压力系数小于升力面压力系数，即桨叶背风面压力系数大于迎风面压力系数，螺旋桨产生与飞行方向一致的正拉力;在桨根部位叶素升力面和吸力面的压力系数相差不大，随着桨径的延伸，在桨尖部位，叶素升力面压力系数与吸力面压力系数之间的差别越来越大，这是由于合成气流的速度大小和攻角都随着桨径的延伸而逐渐增大的原因。

由图6(c)可见，当转速继续增大到1200 rpm时，桨叶迎风面与背风面的压力系数之差越来越大，但桨根部位叶素升力面和吸力面压力之差依然很小;随着桨径的延伸，叶素升力面和吸力面压力之差逐渐增大，当桨径延伸到一定程度后，叶素升力面和吸力面压力之差又逐渐变小，这可能是由于转速增大，在桨尖部位存在诱导激波的原因。

比较图6(a)、(b)、(c)可知，当前进速度不变，螺旋桨转速增大时，叶素升力面和吸力面压力之差越来越大，说明桨叶产生的拉力随着转速的增大逐渐增大。由叶素三角形理论［19］可知，当螺旋桨前进速度不变且转速增大时，合成气流相对于叶素的速度和攻角逐渐增大，因此桨叶产生的拉力逐渐增大，仿真结果与图5(a)和理论分析一致。

图7是螺旋桨前进速度为20 m/s，转速分别为300 rpm、900 rpm和1500 rpm时，部分叶素周围流线分布比较图。由图7(a)可见，当转速为300 m/s时，从桨根到z=0.1 m处的桨径区域，叶素处于负攻角状态，说明有一部分叶素产生负拉力，这将减小螺旋桨的总拉力，从而降低螺旋桨气动性能，导致气动效率降低。由图7(b)可见，当转速增大为900 rpm时，螺旋桨桨根部位流动非常稳定，但从z=0.2 m处，桨叶表面开始出现流动分离现象，当桨径继续延伸时，分离现象逐渐加剧。流动分离的存在将会大大降低螺旋桨的气动性能，尤其是降低螺旋桨的气动效率。由图7(c)可见，当螺旋桨转速继续增大到1500 rpm时，在z=0.1 m的桨径部位，叶素周围就开始出现了流动分离现象，而且分离涡随着桨径的延伸迅速增大，分离现象比转速为900 rpm时严重很多，说明此时螺旋桨的气动性能低于转速为900 rpm时。因此，螺旋桨效率随转速先提高后降低的原因是:当转速很小的时候，由于桨叶部分叶素处于负攻角状态导致效率降低，当转速很大时，由于桨叶部分叶素处于大迎角工作状态，叶素表面流动分离严重，导致螺旋桨气动效率降低。

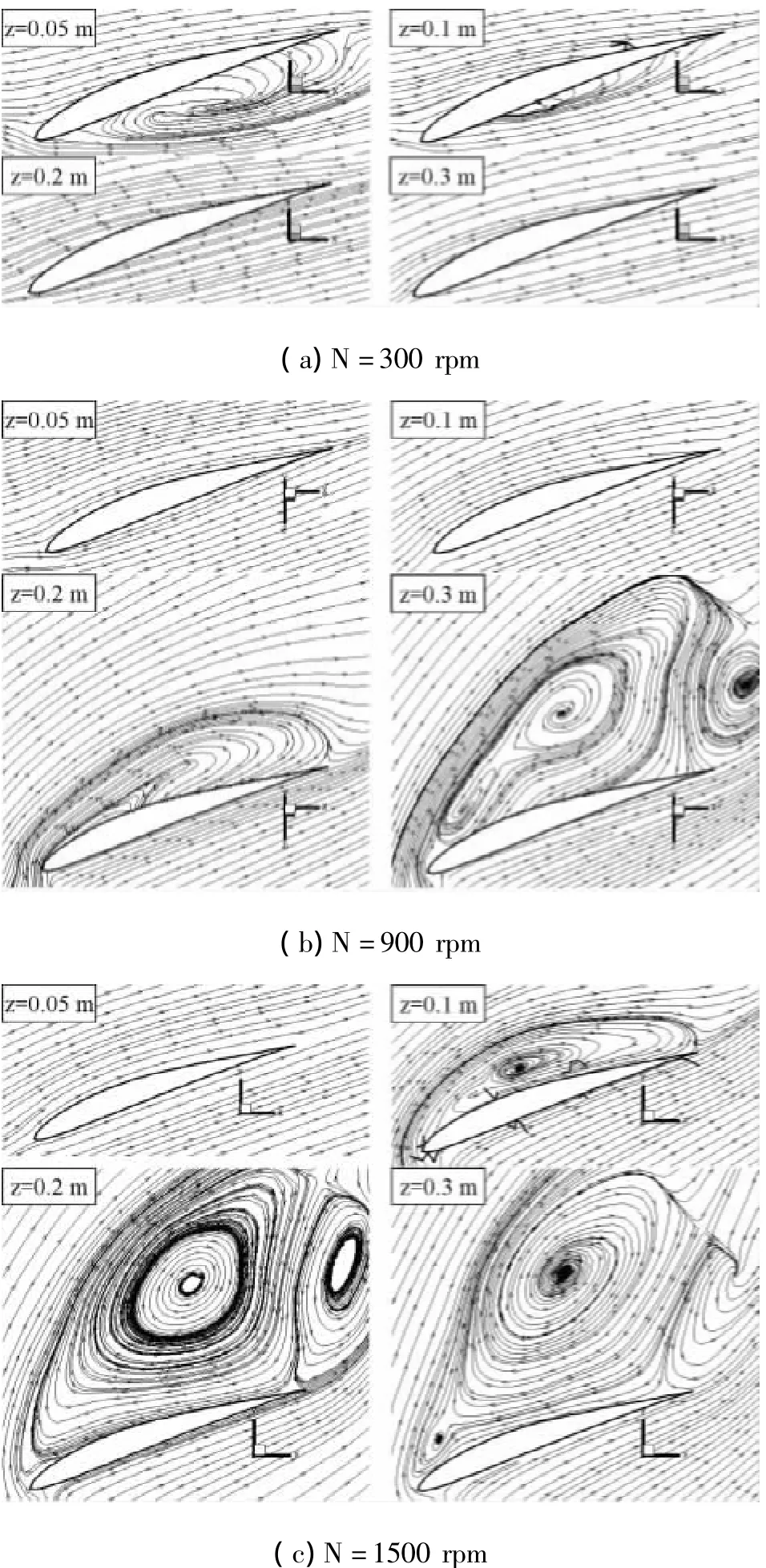
图7 前进速度20 m/s时叶素周围流线分布比较图

图8是前进速度为5 m/s，转速分别为60 rpm、180 rpm和1200 rpm时，x=0的横截面上，流场速度和涡流强度分布比较图，其中速度单位为m/s，涡流强度的单位为1/s。由图8(a)可见，当转速为60 rpm时，流场的速度很小，桨尖部位的气流速度甚至小于桨根部位的速度，且桨根部位速度场的分布范围也大于桨尖部位;涡流强度与速度分布一样，桨根部位的涡流强度大于桨尖部位。由图8(b)可知，当转速增大到180 rpm时，桨尖部位的速度大于桨根部位，桨尖部位速度场的分布范围也大于桨根部位;涡流强度与速度分布一样。由图8(c)可见，当转速继续增大到1200 rpm时，桨尖部位的速度进一步增大，速度场的分布范围也在增大，两个桨叶速度场之间逐渐开始相互影响;涡流强度大小及分布与速度分布相同。比较图8(a)、(b)、(c)可知，桨叶周围速度及速度场的分布范围，涡流强度及涡流强度分布范围都随转速的增大而增大。

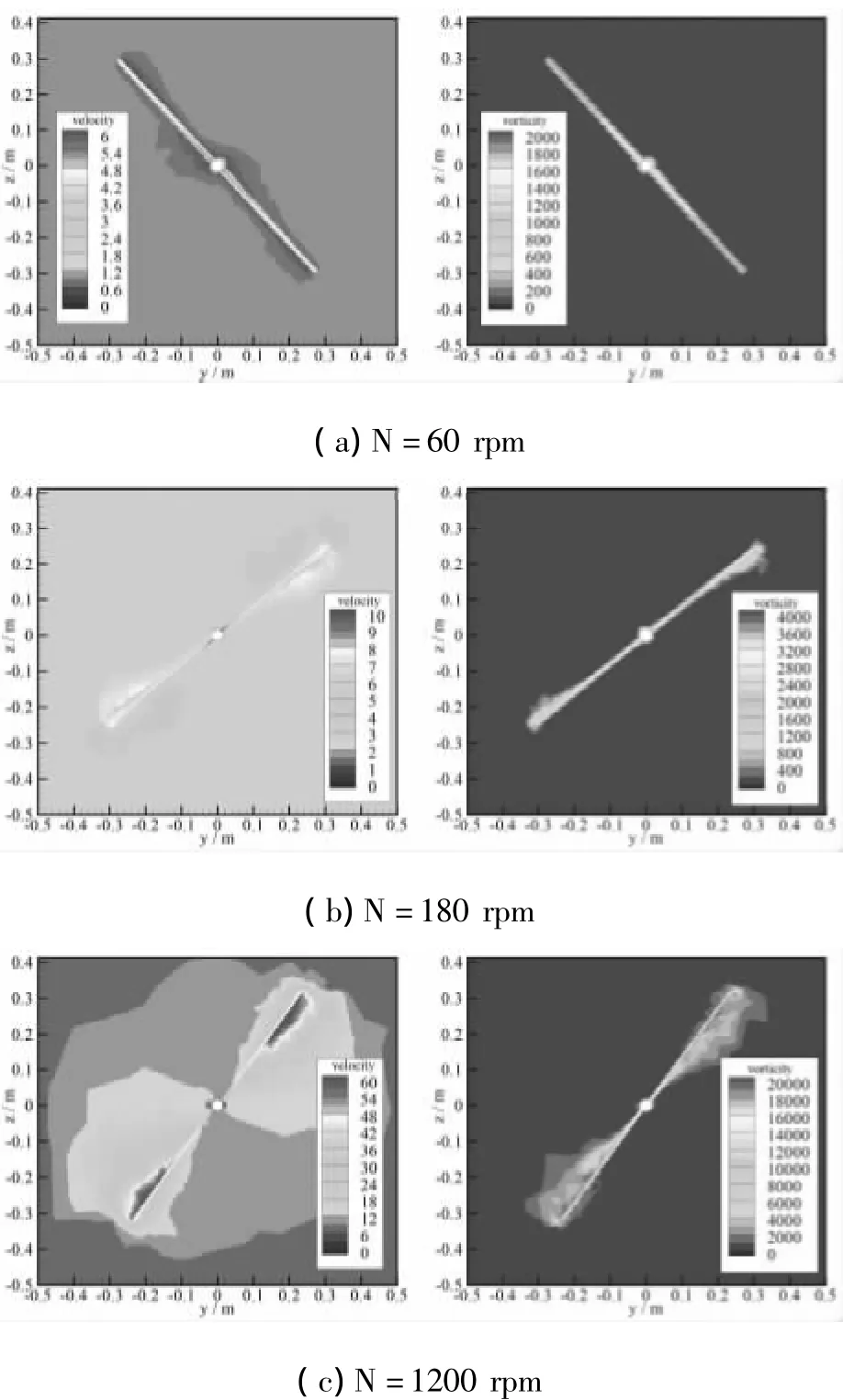
图8 前进速度为5 m/s时x=0处速度和涡量分布比较图

图9是前进速度5 m/s、转速1200 rpm时，流场速度分布沿气流方向的演化图，速度单位是m/s。螺旋桨中心位置在x=0的地方，因此x小于0的横截面在螺旋桨前进方向，x大于0的横截面在螺旋桨的后面。由图可见，在螺旋桨的前面，由螺旋桨桨叶转速运动产生旋转诱导速度的影响范围较小，在x=-0.2的地方速度场的分布范围就已经比较均匀。当x逐渐增大至靠近螺旋桨，即靠近x=0的横截面时，速度场的分布变得越来越不均匀，由桨叶旋转运动产生的旋转流场对气流的影响越来越大，并且逐渐变成由旋转诱导速度为主。在x=0的横截面上诱导速度的影响范围最大，最大诱导速度在螺旋桨桨尖部位。当x继续增大时，旋转诱导速度对气流的影响又逐渐减小，至x=0.7 m处旋转诱导速度的影响不明显，可见在螺旋桨的后面，旋转诱导速度的影响范围远大于前面的影响范围。

4 结论

本文基于滑移网格模型，考虑RNG k-ε湍流模型，通过求解三维非定常N-S方程，在验证了数学模型可行性的基础上，仿真研究了螺旋桨非定常旋转流场。所得流场清晰，速度、流线、涡流强度等流场参数分布正确，仿真结果与文献资料和理论分析一致，可以用于临近空间螺旋桨的设计和研究。主要结论有:

1)当螺旋桨前进速度不变，转速增大时，合成气流相对于叶素的速度大小和攻角逐渐增大，所以螺旋桨总拉力随转速的增大而增大。

2)当螺旋桨前进速度不变时，转速很小则有一部分桨叶叶素处于负迎角状态，导致效率降低;转速很大则有一部分桨叶叶素处于大迎角状态，叶素表面流动分离严重，导致效率降低;所以螺旋桨的效率随转速的增大先提高后降低。

3)桨叶周围速度大小及速度场的分布范围、涡流强度大小及涡流强度分布范围都随转速的增大而增大。

4)桨叶旋转运动产生的诱导速度对螺旋桨前面流场的影响范围较小，对螺旋桨后面流场的影响范围较大。

参考文献:

［1］Arne S.Unsteady CFD Simulations of Contra-Rotating Propeller Propulsion Systems［C］//Hartford，44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference＆Exhibit.2008，AIAA 2008-5218.

［2］阎超，于剑，许晶磊，等.CFD模拟方法的发展成就与展望［J］.力学进展，2011，41(5):562-589.

［3］徐国华，招启军.直升机旋翼计算流体力学的研究进展［J］.南京航空航天大学学报，2003，35(3):338-344.

［4］Caradonna F X，Dessopper A，Tung C.Finite difference modeling of rotor flow including wake effects［J］.Journal of the American Helicopter Society，1984，29(2):86-33.

［5］Chang I C.Transonic flow analysis for rotors，Part 1:Three-dimensional quasi-steady full-potential calcula-tion［R］.NASA TP-2375，1984.

［6］Egolf T A，Sparks S P.A full potential rotor analysis with wake influence using all inner-outer domain techmque［C］.//In the 42th AHS Annual Forum，1986.

［7］Steinhoff J，Ramachandran K.Free wake analysis of compressible rotor ftows［J］.AIAA Journal，1990，88(3):426-431.

［8］王适存，徐国华.直升机旋翼空气动力学的发展［J］.南京航空航天大学学报，2001，33(3):203-211.

［9］杨国伟，何植岱.计及尾涡收缩的螺旋桨滑流计算［J］.空气动力学学报，1995，13(1):83-86.

［10］王立群，乔志德，钟伯文.直升机旋翼悬停流场的欧拉方程计算［J］.空气动力学报，1998年，16(3):282-287.

［11］王立群，乔志德，张茹.直升机旋翼悬停流场的欧拉方程计算［J］.西北工业大学学报，1998年，16(4):594-598.

［12］杜朝晖.水平轴风力涡轮设计与性能预估方法的三维失速延迟模型 -Ⅰ理论基础［J］.太阳能学报，1999，20(4):392-397.

［13］杜朝晖.水平轴风力涡轮设计与性能预估方法的三维失速延迟模型-Ⅱ模型建立及应用［J］.太阳能学报，2000，21(1):1-5.

［14］聂营，王生，杨燕初.螺旋桨静推力数值模拟与实验对比分析［J］.计算机仿真，2009，26(3):103-107.

［15］聂营.平流层飞艇高效螺旋桨设计与试验研究［D］.中国科学院光电研究所硕士学位论文，2008.

［16］许建华，宋文萍，韩忠华.基于嵌套网格技术的风力机叶片绕流数值模拟［J］.太阳能学报，2010年，31(1):91-94.

［17］许建华，宋文萍，韩忠华，杨旭东，基于CFD技术的螺旋桨气动特性研究［J］.航空动力学报，2010年，第25卷第5期，1103-1109.

［18］罗淞，杨永，左岁寒.螺旋桨流场Euler/NS数值解对比分析［J］.航空计算技术，2011，41(1):74-77.

［19］程钰锋，聂万胜.临近空间螺旋桨气动性能分析［J］.直升机技术，2011，168:8-13.

［20］Yakhot V，Thangam S，Gatski T B，Orszag S A，Speziale C G.Development of Turbulence Models for Shear Flows by a Double Expansion Technique［R］.NASA Contractor Report 187611，ICASE Report No.91-65.

［21］Rubinstein R. Renormallzation Group Theoryof Bolgiano Scaling in Boussinesq Turbulence［R］.NASA Technical Memorandum 106602，ICOMP-94-8;CMOTT-94-2.

［22］Scandaliato A L.AUSM-based high-order solution for euler equations［C］//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition 4-7 January 2010，Orlando，Florida，AIAA 2010-719.

［23］Thompson.J.F.，Thames.F.C.，Martin.C.W.Automatic Numerical Generation of Body-Fitted Curvilinear Coordinate System for Field Containing Any Number of Arbitrary Two-Dimensional Bodies［J］.J.Comput.Phys.1974(15):299-399.