Marcinkiewicz积分交换子的Sharp极大函数估计和连续性
赵 妍,王小珊
(1.皖南医学院 基础部,安徽 芜湖 241002;2.安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)
Marcinkiewicz积分交换子的Sharp极大函数估计和连续性
赵 妍1,王小珊2
(1.皖南医学院 基础部,安徽 芜湖 241002;2.安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)
文章主要研究了Marcinkiewicz积分交换子与加权Lipschitz函数在加权 Lp空间中的Sharp极大函数估计和连续性.
Marcinkiewicz积分交换子;加权Lipschitz函数;Sharp极大函数
1 引言
设 Sn-1是Rn(n≥2)上的单位球面,Ω∈L1(Sn-1)是零次齐次函数且满足

定义Marcinkiewicz积分
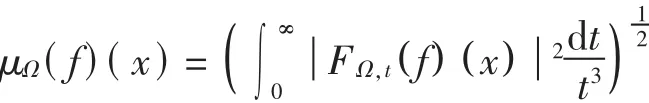
其中

设 b是一个局部可积函数,由 μΩ和 b生成的Marcinkiewicz积分交换子定义为
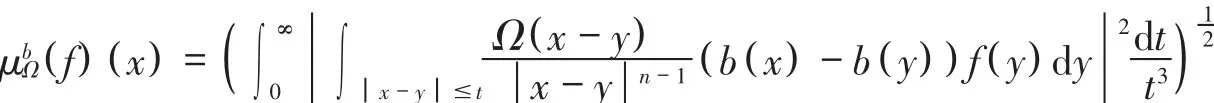
关于 μΩ及有着丰富的结果.2011年,文[1]研究了Marcinkiewicz算子交换子与加权BMO函数的 Lp(α)的有界性,同时,文[2]研究了强奇异积分算子的多线性交换子的Sharp极大函数估计和连续性.最近,Lee和Rim在消失性条件(1)和某种对数型Lipschitz条件下得到了Marcinkiewicz积分的一些性质[3],这种对数型条件比之前的Lipschitz条件更弱,叙述如下:令 n≥2,若存在 c>0及 δ>1,使

对 y1,y2∈Sn-1一致成立,则称(2)为对数型条件.
基于这些工作,本文利用Sharp极大函数技术研究了Marcinkiewicz与加权Lipschitz函数在 Lp空间的有界性.
2 预备知识及定理
本文中,Q表示Rn中的方体,kQ表示与 Q同中心,边长为其 k倍的方体,记 Qk=2kQ.给定方体 Q和局部可积函数 f,令


Ap权定义为:对于1<p<∞

A(p,q)定义为:对于1<p,q<∞

注1 由Hölder不等式,可以得到 A(p,q)⊂Ap,1<p,q<∞.
给定权函数 w,对1<p<∞,加权Lebesgue空间 Lp(w)定义为满足以下条件的函数 f:

对0<β<1,加权Lipschitz空间 Lipβ(w)定义为满足以下条件的函数 b的全体:

注2 (1)若 b∈Lipβ(w),w∈A1,x∈Q,则

(2)若 b∈Lipβ(w),w∈A1,则对任何 Q

文[1]研究了在(1)(2)条件下Marcinkiewicz积分与 b∈BMO((αβ-1)1/p)生成的交换子是从 Lp(α)到 Lp(β)的有界算子.文[2]研究了强奇异积分算子与 b∈Lipβ(w)生成的多线性交换子从 Lp(w)到 Lq(w1-mq)的有界性.受其启发,本文得到如下结果:




3 定理的证明
为证明定理,需要下列引理.




引理3[4,6]对任意方体 Q,b∈Lipβ(w),0<β<1,w∈A1,有

引理4[7](Kolmogoro不等式) 设 S是弱(1,1)型算子,0<γ<1,|E|<∞,则存在一个仅依赖于 γ的常数,使得

引理5 若 w∈A1,则对 r>1及任何方体 Q,有
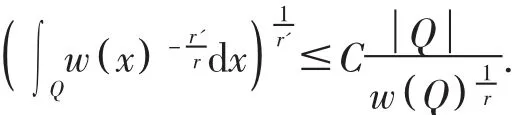
证明 由 Ap权的性质知,对于 r>1及 w∈A1有 w∈Ar,据 Ap权定义知,对任何方体 Q,有

即
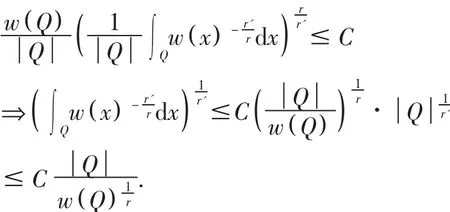
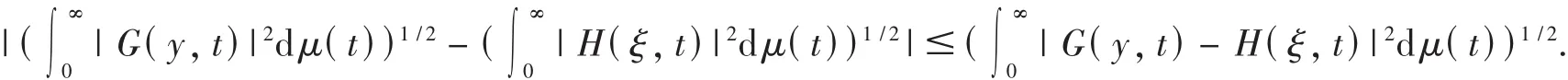
引理7 设 f∈Lloc(Rn),则|f(x)|≤Mη(f)(x),(η>0),a.e.
证明 由 Lebesgue微分定理知
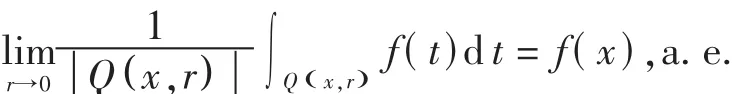
而

上式两边关于 r取极限(r→0)得:
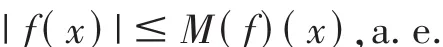
从而,对于 η>0,有:
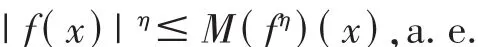
故

定理1的证明 我们只需证明对任意方体 Q,有

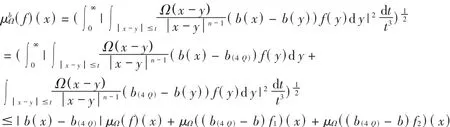
故
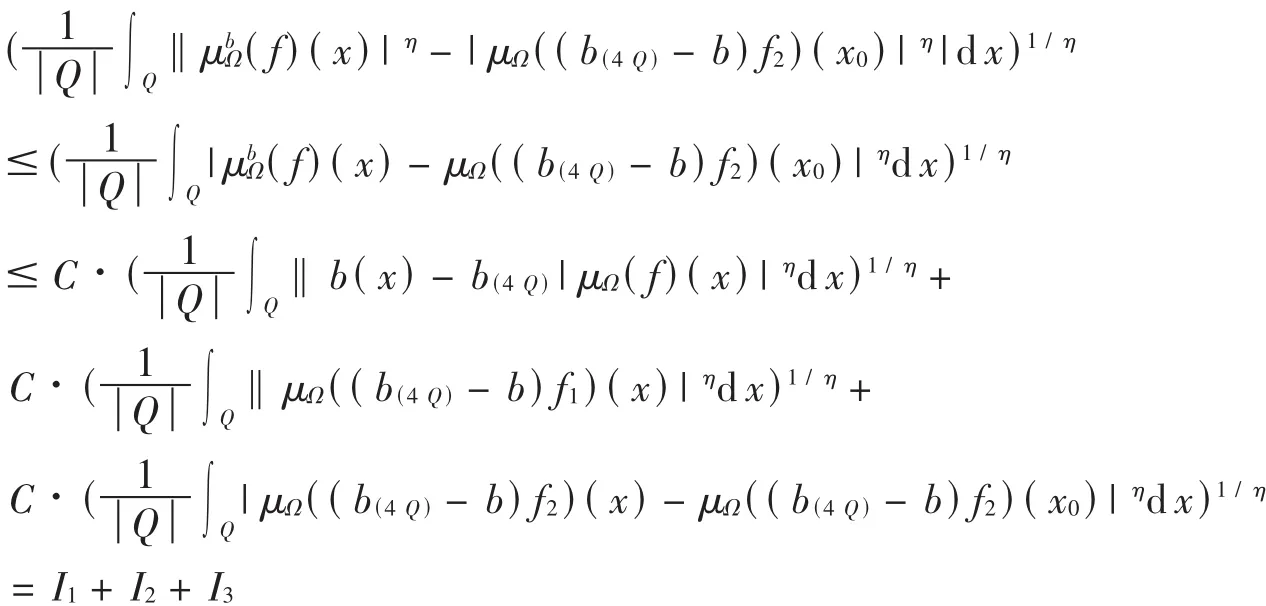
对于 I1,选取 r>1,由Hölder不等式,

由引理3及引理5得:
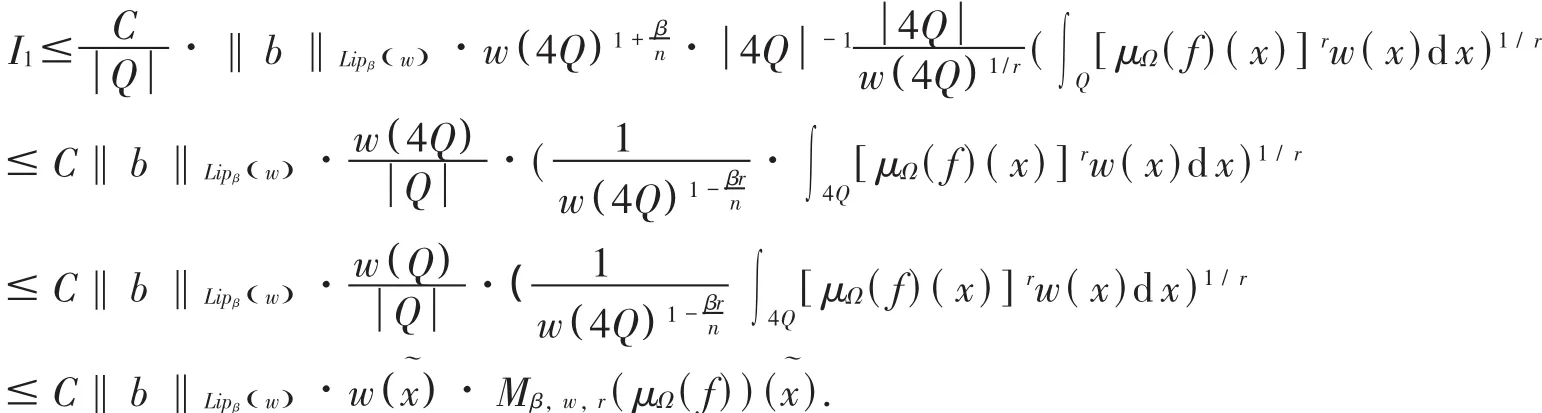
对于 I2,由 μΩ的弱(L1,L1)有界性及Kolmogoro不等式有:
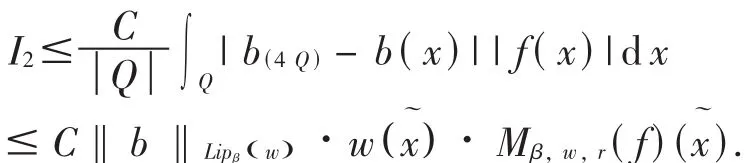
对于 I3,我们记

由引理6,得:


对于 J1,Ω有界,当 x,x0∈Q,z∈(4Q)c时,|z-x|~|z-x0|,由Marcinkiewicz积分不等式:

而
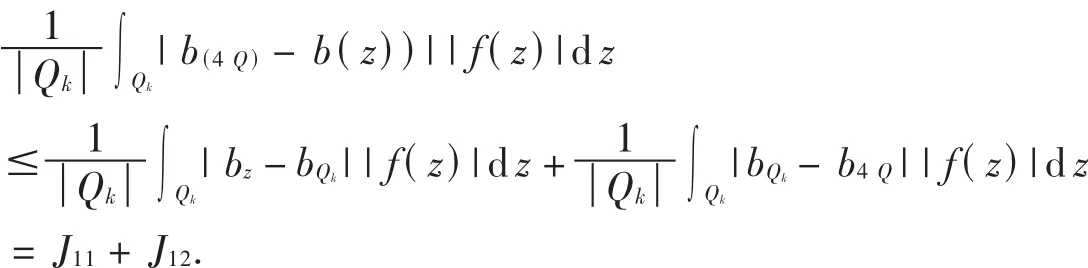
对于 J11,类似于 I1可得:

对于 J12,由注1(1)及Hölder不等式可得:

所以

对于 J2,类似于 J1可得:

下面估计 J3:当 x,x0∈Q,z∈(4Q)c时,有|z-x|~|z-xo|,所以
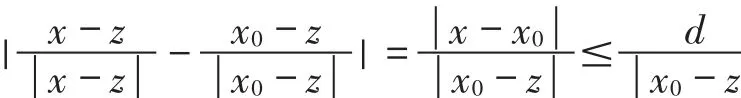
由条件(1.2)知:
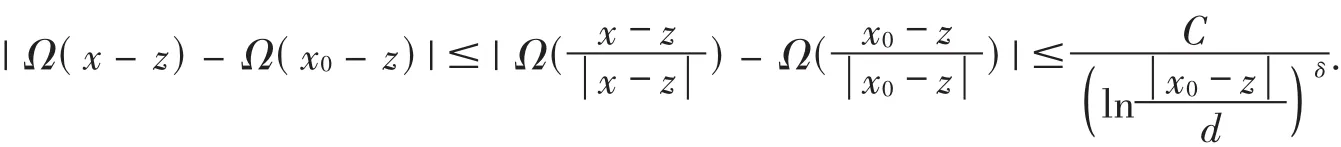
所以
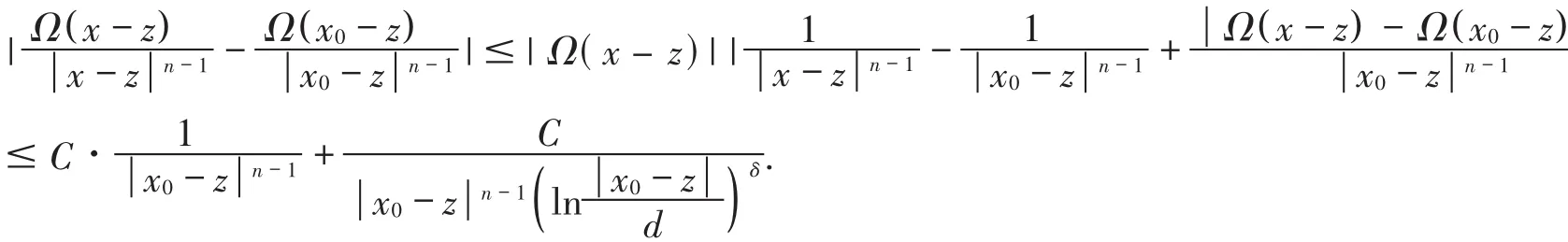
由Minkosvski不等式,得:

类似于 J1的估计可得:
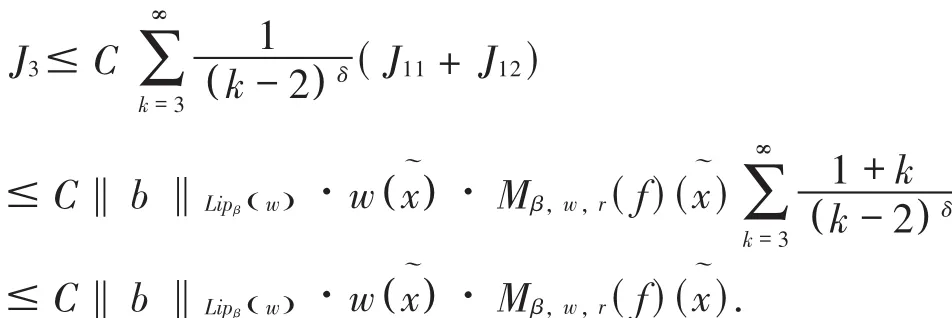
因此由Hölder不等式可得:
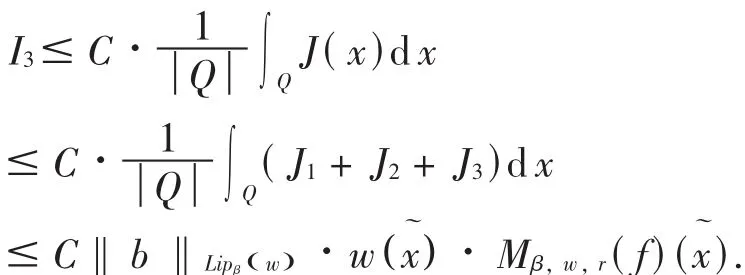
证毕!
定理2的证明 在定理1中选取 r<p,由引理1,7,2可得:

证毕!
致谢:感谢导师安徽师范大学数学计算机科学学院束立生教授的悉心指导!
[1]何月香,王月山.Marcinkiewicz积分交换子与加权BMO函数[J].数学学报,2011,54(3):513-520.
[2]刘岚吉吉.强奇异积分算子的多线性交换子的Sharp极大函数估计和连续性[J].数学学报,2011,54(3):503-512.
[3]LEE J,RIM K S.Estimates of Marcinkiewicz integrals with bounded homogeneous kernels of degree zero[J].Integr equ oper theor 2004,48(2):213-223.
[4]GARCIA-CUERVA J,RUBIO de FRANCIA J L.Weighted norm inequalities and related topics,North-Holland math studie [M].Amsterdam:North-Holland Publishing Co,1985.
[5]MUCKENHOUPT B,WHEEDEN R L.Weighted norm inequalities for fractional integral[M].Trans Amer Math Soc,1974,192 261-274.
[6]GARCIA-CUERVA J.Weighted Hp spaces[J].Dissert Math,1979,162:1-45.
[7]JAVIER Duoandikoetxea.Fourier analysis[M].Trans Spanish,1995:102.
Abstract:In this paper,we mainly discuss the Marcinkiewicz integral commutators with weighted Lipschit functions in weighted Lpspace Sharp maximal function estimates and continuity.
Key words:Marcinkiewicz integral commutator;weighted Lipschitz function;Sharp maximal function
Sharp M aximal Function Estimate and Continuity for Commutators of M arcinkiew icz Integrals
ZHAO Yan1,WANG Xiao-shan2
(1.Department of Basic Courses,Wannan Medicial College,241002,Wuhu,Anhui,China; 2.College of Mathematics and Computer Science,Anhui Normal University,241003,Wuhu,Anhui,China)
O 174.2
A
2095-0691(2012)03-0008-07
2012-06-14
国家自然科学基金资助项目(11101001)
赵 妍(1981- ),女,安徽当涂人,助教,研究方向:调和分析.

