综合监测民生指数的数学模型

陈云

(黎明职业大学 公共教学部，福建 泉州 362000)

综合监测民生指数的数学模型

陈云

(黎明职业大学 公共教学部，福建 泉州 362000)

文章采用分组主成分分析法，在尽量不丢失原有信息的基础上进行指标降维处理;利用网络分析法确定各指标权重，建立综合监测民生指数的数学模型;利用该模型计算泉州市10年的民生指数.得出民生指数监测体系是一个复杂的、多层次的综合监测体系，需要运用科学的监测方法对民生指数做出客观的监测;利用该方法建立民生指数监测模型是可行的.

民生指数监测指标体系;主成分分析法;网络分析法;数学模型

《中华人民共和国国民经济和社会发展第十二个五年规划纲要》中明确指出“坚持民生优先，完善就业、收入分配、社会保障、医疗卫生、住房等保障和改善民生的制度安排，推进基本公共服务均等化，努力使发展成果惠及全体人民”.由此可见，保障和改善民生被放在了一个更加突出的位置.民生工程建设是一个庞大的系统建设工程，在全面深入落实科学发展观的同时，迫切需要一套可以将民生问题指标化、数量化的监测体系，以便适时从科学发展观的角度对民生问题进行综合监测.所谓的民生指数，就是通过建立一套完整的指标体系，通过定量的方法对这套指标体系进行综合测算，从而对人民实际生活质量状况有一个更全面、准确、科学地把握，为政府部门正确的决策提供重要依据.

1 民生指数监测指标体系

1.1 监测指标体系建立的原则

要使评价指标体系能够科学地、准确地反映人民实际生活各方面的景气程度，并对其进行综合监测，所选取的指标须遵循以下原则:(1)科学性.民生指数监测指标体系的结构要科学合理，能客观准确地反映民生指数的内涵，保证民生指数测算结果的真实性与客观性.(2)综合性.评价指标的选取应具有较强的综合性，能够综合反映人民生活的总体状况，突出与民生问题有关的各个重要方面，力求做到不重不漏.(3)可比性.指标的选取应符合客观实际，数据资料可比性强，以便于地区内部和地区之间的比较，可以帮助各地区找出差距.(4)可测性.民生指数监测体系包括客观指标和主观指标，对于客观指标应有稳定的符合客观实际水平的数据来源;对于所选取的主观指标应容易组织实施调查，并且易被受访者所理解、认知、接受并形成及时有效的反馈.

1.2 监测指标体系的初步选定

对民生指数进行综合监测，有助于及时、正确地判断出政府公共服务薄弱环节，进一步为保障和改善民生提供科学依据，因此对民生指数的研究至关重要.有关民生指数的概念，邓平[1]指出，中国民生指数的内涵包括3个方面:物质和财富的增长是民生与民富的重要基础;环境与生态的优化，是民生的基本条件;政府提供卓有成效的公共产品和公共服务是保障以人为本社会公平的重要条件.沙杰等[2]认为，民生统计指标体系的基本框架应由教育、就业和收入、医疗、社保、居住、稳定和谐等6大领域，38个指标组成.严卫华[3]认为，设置民生指数的框架和指标体系社会财富、人口素质、生活水平、生态环境、社会保障、社会安全和公益事业等七大领域，27个指标组成.

结合以上学者的分析，可以发现，各民生指数监测体系均包含了社会公众最为关注的就业、收入、教育、社会保障和社会安全等基本层面的内容.同时，通过深入的调查研究发现，合理民生指标体系的设置不仅要考虑客观的外部指标变量，而且要考虑主观的指标变量，例如民众个体满意度等，因此本文中设置了由客观指标与主观指标组成的民生指数监测指标体系.该体系由7个方面组成一级指标体系，即收入分配与就业B1、环境资源B2、社会安全B3、教育文化B4、医疗卫生B5、公共服务B6和社会保障B7，遵循监测体系建立的原则，每个一级指标又可以细化出若干个二级指标，共54个二级指标.

2 研究方法

根据对相关文献的研究发现，大部分对民生指数的研究只局限于定性的研究，对于民生指数具体定量算法的研究几乎是个空白.本文将采用分组主成分分析法与网络分析法相结合建立数学模型，从定量的角度对民生指数进行综合监测.

2.1 主成分分析法(PCA)

主成分分析主要是一个降低原始数据维数的过程，其目的是运用线性变换，将原来的多个指标组合成相互独立的少数几个能充分反映母体信息的指标，即用较少的指标来代替和综合反映原来较多的信息.这些综合后的指标就是原来多指标的主要成分，从而避开了变量之间共线性的问题[4].主成分分析所提取出的每个主成分都是原来多个指标的线性组合，比如有 p个原始变量 x1，x2，…，xp，则可提取出 p个主成分，如下:

原则上，提取出的主成分个数不多于原始数据的维数，一般提取已包含80%～90%以上信息的前几个主成分，其主要步骤是:

(1)计算相关系数矩阵 R

(2)计算特征向量

用Jacobi法对特征方程|λI－R|=0进行计算，求出特征值 λi(i=1，2，…，m)，使得 λ1≥λ2≥…≥λm≥0.

(3)计算主成分贡献率及累计贡献率.

(4)计算主成分荷载矩阵.

2.2 网络分析法

网络分析法(ANP)是美国匹兹堡大学Satty教授在1996年提出的一种适应非独立递阶层次结构的系统决策方法，特别适用于对存在内部依存和反馈效应的复杂网络结构进行系统的决策.ANP的递阶层次结构划分为两大部分，第一部分称为控制因素层，包括研究目标及决策准则，不一定每个层次结构都必须含有决策准则，但决策目标至少有一个，所有决策准则彼此独立且只受目标元素支配.第二部分称为网络层，由所有受控制层支配的元素组成的，元素之间及内部具有相互依存、相互支配的网络结构关系.进行ANP分析过程中有一个重要步骤就是在一定准则下，各指标元素需进行两两比较，从而获得判断矩阵，由于ANP结构是一个较复杂的网络结构，因此判断矩阵的获得主要通过直接优势度比较和间接优势度比较，前者适用于指标元素之间相互独立，而后者则适用于指标元素间相互依存和反馈的情况[5].

综合监测民生指数的ANP法的基本步骤为:

(1)构建民生指数监测指标体系的ANP网络结构模型.

(2)利用直接优势度和间接优势度比较构造判断矩阵群.控制层中的元素 a1，a2，…，an在以民生指数目标为准则进行直接优势度比较，采用1～9标度对各元素的重要性程度赋值;网络层有 B1，B2，…，BN，其中Bi中有元素 ei1，ei2，…，eini，i=1，2，…，N.以控制层元素 as(s=1，2，…，m)为准则，以 Bj中元素 ejk(k=1，2，…，nj)为次准则，将元素组 Bi中元素 eik(k=1，2，…，ni)按其对 Bj中元素 ejk的影响力大小进行间接优势度比较，最后可获得判断矩阵群.

(3)通过对各判断矩阵进行计算，得到超矩阵.由判断矩阵可计算出归一化特征向量并得到 Wij.

Wij的列向量指的是 Bi中的元素 ei1，ei2，…，eini对 Bj中元素 ej1，ej2，…，einj的影响程度所得到的排序向量.如果 Bj中元素不受 Bi中任何元素影响，则 Wij=0.对于 i=1，2，…，N;j=1，2，…，N的情况，重复上述步骤，最终可获得超矩阵 W[6].

(4)进一步对超矩阵进行加权计算，得到加权超矩阵和极限超矩阵，从而得到各指标元素的权重.有了权重便可以把原始数据标准化后利用加权均值法算出民生指数综合监测值.

3 泉州市民生指数实证分析

3.1 指标数据的采集及处理

以泉州为例对民生指数综合监测模型进行研究，考虑到民生指数监测体系中有客观和主观两种指标.对于客观指标数据主要是通过对2002－2011年《泉州统计年鉴》和《泉州市国民经济和社会发展统计公报》中所获取的数据进行计算整理而得.对于主观指标数据则是通过问卷调查获取相关数据，在本课题组成员及学生的共同协助下，共发放500份问卷调查，实际回收446份，回收率为89.2%，其中有效问卷430份，此次调查的范围较广，并且调查对象的选择也具有代表性和广泛性.

综合监测民生指数的目的是要用一个综合数值对民生质量的好坏进行全面描述，指标之间须具有可比性，但本文所选择的指标量纲是不同的，因此需要转换相应的指标，以消除量纲，便于统一运算.在进行主成分分析时，SPSS软件会自动用Z－Score对原始数据进行无量纲化处理.

3.2 主成分分析法确定评价指标体系

前面所确定的民生指数监测体系中包含7个一级指标和54个二级指标，考虑到二级指标比较多，而且这些指标间可能存在着一定的相关性.为了对数据有一个大致的了解，可采用主成分分析法对数据进行分析.但是，如果直接用主成分分析法对二级指标提取主成分会比较复杂而且往往达不到理想的结果，因此可考虑先分组进行主成分分析，即对每个一级指标下的二级指标进行主成分提取，在此只取第一主成分.下面以医疗卫生为例进行说明，将获取的医疗卫生各指标数据存放到SPSS软件中，进行相关性分析(见表1)，检验是否有进行主成分分析的必要.

从表1可以看出每万人拥有医疗床位数与城镇每万人口医生数这两个变量的相关系数较大(0.907)，且Sig值为0.000，说明这两个变量之间存在高度相关性.同样可以判断人均地方财政一般预算内卫生服务投入与城镇每万人口医生数这两个变量也显著相关，因此有必要进行主成分分析.公因子方差(见表2)表明大部分指标变量共同度的取值均在0.7以上，这说明提取出来的主成分对原始指标变量的解释效果不错.表3给出了医疗卫生组中提取出来的第一主成分所解释的方差已经达到71.031，说明提取出来的第一主成分能够解释原始变量所包含的近70%的信息量.从表4中可以看出第一主成分在城镇每万人口医生数与人均地方财政一般预算内卫生服务投入这两个变量上有较大的荷载，因此医疗卫生组中选择“城镇每万人口医生数”与“人均地方财政一般预算内卫生服务投入”这两个指标变量.同样的分析方法可以对其他6组一级指标用主成分分析法把第一主成分提取出来(需考虑第一主成分的方差贡献率，如果贡献率较大，才可用这种方法)，然后把对第一主成分有较大荷载的变量选出来，这样降维的目的就达到了，而且具有较科学的理论支持.由于篇幅受限，其它各组的主成分分析输出结果包括特征值、方差贡献率(各组第一主成分的方差贡献率均大于65%)和累计方差贡献率等均不列出.

表1 医疗卫生指标下各二级指标相关性矩阵

表2 公因子方差

表3 解释的总方差

表4 医疗卫生指标下二级指标的成分矩阵a

通过分组主成分分析法最终确定民生指数监测指标体系如下:

收入分配与就业B1=(全市新增劳动力就业岗位数B11，城镇居民人均可支配收入占人均GDP比重B12，农村文化教育娱乐支出占家庭消费支出比重B13)

环境资源B2=(人口密度B21，城镇居民人均住房建筑面积B22，建成区绿化覆盖率B23，市容环境卫生公共满意度B24)

社会安全B3=(食品、药品公众安全满意度B31，居民社会安全感满意度B32，万人口交通事故死亡率B33)

教育文化B4=(九年义务教育完成率B41，初中师生比B42，每万人中在校大学生数B43)

医疗卫生B5=(城镇每万人口医生数B51，人均地方财政一般预算内卫生服务投入B52)

公共服务B6=(公交运营线路网长度B61，政府廉政及行政效率满意度B62，人均公共图书馆馆藏图书B63)

社会保障B7=(社会保障和就业支出占财政支出比重B71，全市年底基本医疗保险人数B72)

3.3 网络分析法确定民生指数监测模型

对所提取的指标变量进行分析发现，各个指标变量不全是相互独立，而是具有一定的依存和影响关系.如B41与B43、B23与B24、B71与B72等都存在着影响关系.还可以发现，不是同一个一级指标中的变量也存在着影响关系，如B24与B52、B11与B71等也都有存在影响关系.因此可以确定民生指数监测体系并不是一个内部相互独立的简单的递阶层次结构，而是内部存在着互相依存和反馈的复杂的递阶层次网络结构，因此利用网络分析法确定各指标变量的权重.

经过反复推敲并进行专家访谈，最终给出了综合监测民生指数的ANP网络结构模型，如图1所示.该网络结构中的控制层中没有准则层，只有一个总目标—— 民生指数监测，因此民生指数监测既作为总目标又作为准则.在网络层中包括7个元素组，各元素组之间的相互影响关系都以箭头标出，每个元素组中又有若干个元素，共由20个元素构成.

图1 民生指数监测体系的ANP网络结构

以控制层中总目标为准则，以网络层中元素为次准则，各元素组中的元素进行两两比较.为了较客观、真实、准确地反映元素间的重要性，本课题组共发放400份问卷调查，其中回收的有效问卷359份，有效率达89.8%.问卷要求采用1～9标度对两两相关的元素，在准则和次准则下的重要性进行间接优势度比较，从而获得关系判断矩阵群.接下来需要计算的超矩阵、加权超矩阵和极限超矩阵等相关运算过程均通过super decision软件来完成.由于篇幅有限，判断矩阵群、超矩阵和加权超矩阵本文中不列出来，这里只给出由super decision软件计算出的极限超矩阵 W的一部分，见图2.

图3是利用super decision软件计算得到的二级指标相对权重的输出结果.图3中的第3列给出的是各个二级指标权重的条形图，第4列和第5列分别给出的是该指标的局部权重和全局权重.

图2 极限超矩阵W输出结果

图3 二级指标相对重要性权重输出结果

3.4 泉州市民生指数监测模型的建立

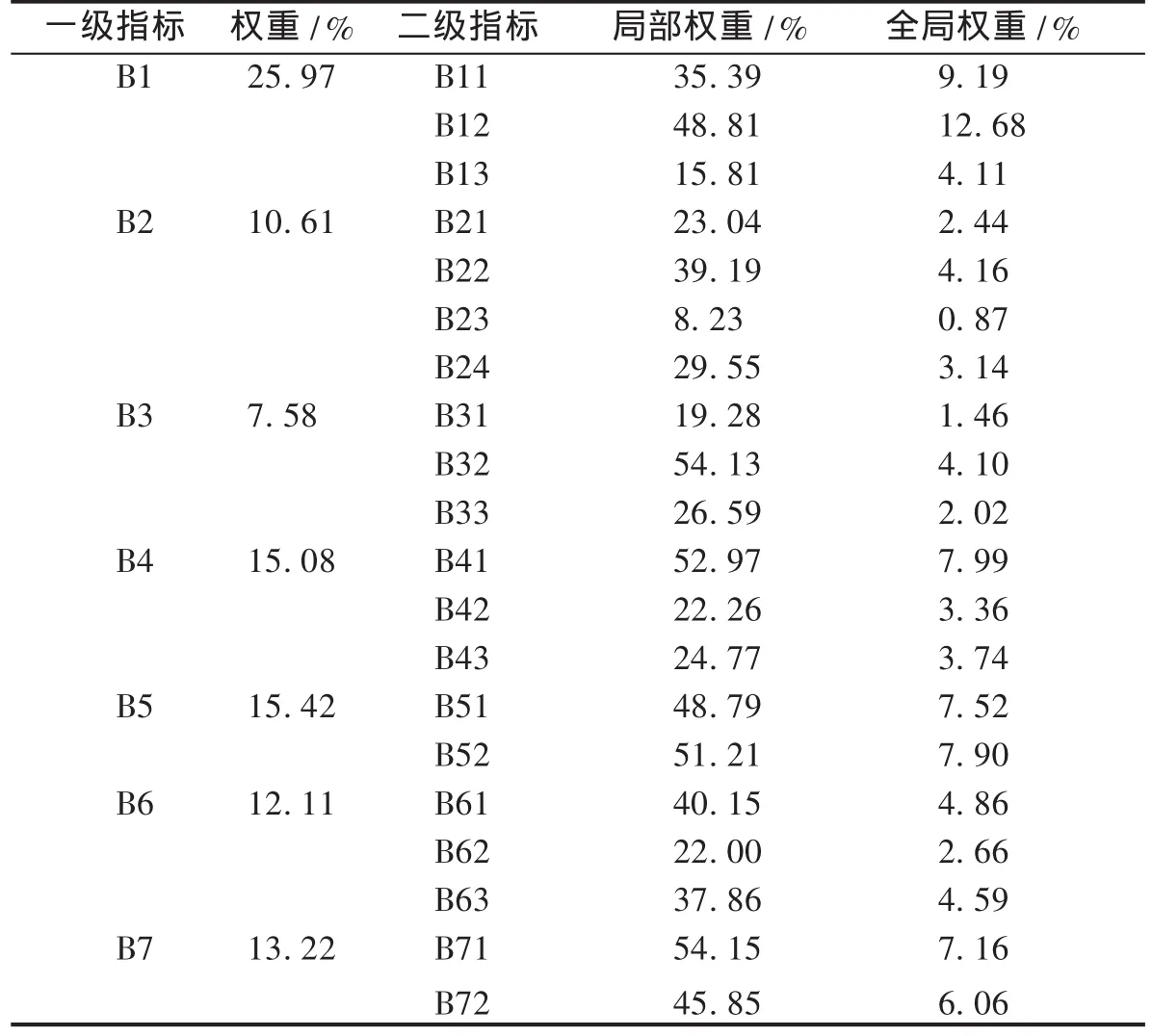
表5 民生指数监测体系指标的局部权重和全局权重

经过整理，表5给出了民生指数监测体系一级指标和二级指标的权重.由此，可以得到7个一级指标变量与其二级指标变量的函数关系式为:

B1=0.353 9B11+0.488 1B12+0.158 1B13

B2=0.230 4B21+0.391 9B22+0.082 3B23+0.295 5B24

B3=0.192 8B31+0.541 3B32+0.265 9B33

B4=0.529 7B41+0.222 6B42+0.247 7B43

B5=0.487 9B51+0.512 1B52

B6=0.401 5B61+0.22B62+0.378 6B63

B7=0.541 5B71+0.458 5B72

最终，可得到综合监测民生指数 A的数学模型为:

民生指数 A=0.259 7B1+0.106 1B2+0.075 8B3+0.150 8B4+0.154 2B5+0.121 1B6+0.132 2B7，其中模型中各指标变量的数值 Bi(i=1，2，…，7)均为原始数值无量纲化后的数值.

3.5 泉州市2002-2011年民生指数监测结果

根据所研究目标的特殊性，采用阈值法对各指标的原始数据进行无量纲化处理，使各指标变量值落在[0，100]区间内，把无量纲化以后的数值代入上述各数学模型，便可以得到每一年度不同指标变量值得分情况，以及每一年度的民生指数综合监测值 A，可以确定 A的取值范围在[0，100]之间，数值越大说明民生指数越高，人民实际生活景气程度越高，政府的民生工程建设做得越到位.具体的监测值见表6所示.

表6 泉州2002—2011年度民生指数监测值

从表6中可清楚的看出每一年泉州民生指数综合监测值 A以及每一年度各个指标变量 Bi(i=1，2，…，7)的监测值.利用这一表格可以方便对各个指标变量值 Bi(i=1，2，…，7)进行横向与纵向的比较，找出优势与不足，便于明确提高民生指数的着力点.可以看出，泉州市民生指数综合监测值 A年年都在提高，说明泉州市民实际生活中各方面的综合景气程度在逐年上升，但是在前5个年度里，民生指数监测值 A均较低，虽然一直有所提高，但是变化不大，总是在(61，70)区间内徘徊.而从2007年开始，泉州民生指数有了大幅度的提高，说明泉州政府的民生工程建设从2007年开始有了较大的发展，这一提高正好与党的十七大步伐相一致，与“十七大”报告中提出的“科学发展观的核心是以人为本，必须在经济发展的基础上，更加注重社会建设，着力保障和改善民生，推动建设和谐社会”相吻合.

4 结论

民生指数对贯彻落实科学发展观，构建和谐社会具有重要的导向作用，对各级政府的宏观决策具有不可或缺的辅助作用.民生工程的建设要有科学的决策依据，这就需要建立完善的民生指数监测指标体系，运用科学的监测方法对民生指数做出客观的综合监测.而民生指数监测体系是一个复杂的、多层次的综合监测体系，因此本文采用分组主成分分析法与网络分析法相结合建立综合监测民生指数的数学模型.实证结果表明，利用该方法建立民生指数监测模型是可行的.

应用该方法具有以下几个优点:首先，可以把影响民生指数的多种因素进行全面分析;其次，可以把反映民生质量问题的多个综合指标根据不同区域民生实际情况，通过降维的思想，在不丢失原有信息的基础上，减少为少数几个综合指标，这样可以便于下一步的分析;最后，利用网络层次分析法获得各指标的权重，建立综合监测民生指数的数学模型，从而获得各指标相对于民生指数影响力的大小，便于对各指标进行纵向、横向分析比较;同时，也使监测结果能够更科学地转化为具体的数值，便于政府及相关部门掌握民生工程建设的进程及成效情况，从而为有针对性的制定相应的对策提供理论依据，促进民生工程进一步发展.

[1]邓平.建立中国民生指数的建议[J].特区实践与理论，2009(2):42－44.

[2]沙杰，杨志刚.民生统计指标体系浅见[J].中国统计，2008(7):56－57.

[3]严卫华.重视民生指数对经济社会发展的导向作用[J].宏观经济管理，2008(3):51－52.

[4]赖国毅，陈超.SPSS17中文版统计分析典型实例精粹[M].北京:电子工业出版社，2010.

[5]SAATY T L.Decision making with dependence and feedback:the analytic network process(Second Edition)[M].Pittsburgh:RWS Publications，2001.

[6]王莲芬，蔡海鸥.网络分析法的理论与算法[C]∥决策科学理论与方法—— 中国系统工程学会决策科学专业委员会第四届学术年会论文集.北京:海洋出版社，2001:9－17.

Abstract:The people's livelihood indexmonitoring system is a complex，multi－layered comprehensivemonitoring system，we need to use scientific methods tomake objective monitoring index of livelihood.This paper constructs the indexmonitoring index system，by grouping principal component analysismethod and analytic network process to establish people's livelihood index comprehensive monitoring model.First of all，by grouping principal component analysis，to try not to lose the original on the basis of information index reduction;then，using the network analysis method to determine the index weight，establishing the comprehensive monitoring index of livelihood mathematicalmodel;finally，using themodel to calculate the Quanzhou city the ten years of the people' s livelihood index.The results show that，using the method to establish the people's livelihood index monitoring model is feasible.

Key words:the people's livelihood index monitoring index system;principal component analysis;network analysis;mathematicalmodel

On M athematical M odel of Integrated M onitoring of the Peop le's Livelihood Index

CHEN Yun
(Department of Public Education，Liming Vocational University，362000，Quanzhou，Fujian，China)

TP 393

A

2095－0691(2012)03－0034－08

2012－06－08

黎明职业大学2011年研究规划课题(LW 2011204)

陈 云(1978－ )，女，福建泉州人，讲师，硕士，研究方向:数学应用.