初中数学课堂实践活动教学实施的思考

◆赵菊平

(苏州市吴江芦墟二中)

初中数学课堂实践活动教学实施的思考

◆赵菊平

(苏州市吴江芦墟二中)

《全日制义务教育课程标准》指出:有效的数学学习不能单纯地依赖模仿和记忆，动手实践、自主探索与合作交流是学生学习数学的重要方法。课堂实践活动是教学的一个环节，也是一种教学方式，其实是一种数学活动，是学生根据已有的数学知识和生活经验，独立或在老师指导下，或小组讨论并借助于一定的物质工具对数学知识结论的探索、验证的过程，也可以是对数学知识的应用过程。重视数学实践活动教学，关注学生发展，它在中学数教学中有以下几方面的作用。

一、操作体验，形成正确的数学观

长期以来，数学无用、数学枯燥难学、数学学习就是“苦读+考试”。数学课就是老师讲学生听、学数学只要一张纸一支笔，数学只是数学家的游戏的观念正在被改变。数学课堂实践活动，改变了数学的学习方式，使学生更加关注数学的理解，关注数学过程、数学的本质。通过数学实践，可以使学生了解数学本质。对于中学生来说也许还不能理解其中所包含全部数学，但至少可以欣赏到由数学产生的美，知道数学枯燥的外表下蕴藏着有趣的、多姿多彩的世界，激发学生的求知欲，使学生体验到数学的优美，体验到数学学习的趣味性，这些都从根本上改变了学生对数学不正确的认识，有利于形成正确的数学观。

二、培养兴趣，树立学好数学的信心

数学实践就是动手算一算、画一画、量一量，一个题目，光想不动手，往往不得其门而入，动手做，常会有启发。譬如:代数问题，把字母代成数试一试，几何问题，多画几个图看一看，这比你冥思苦想效果好得多。如教“轴对称图形”时，组织学生进行折纸、剪纸实验，学生通过折、剪出多种多样的美丽的对称图形，如下图。

看着自己的作品，学生往往会产生一种喜悦的心情，成就感，进而产生强烈的求知欲，从而起到激发兴趣的作用。

三、激活思维，培养学生的创新能力

数学理论的抽象性，通常都有某种“直观”的想法为背景，作为教师，就应该通过数学实践，把这种直观的背景显现出来，帮助学生抓住其本质，了解它的变形和发展及与其它问题的联系，给学生更大的思维空间。例如，你能把一张三角形纸片剪成两个三角形，使它们恰好相似吗?教师就可通过学生的实践操作:剪纸活动，使学生领悟其本质。以一个贴近学生生活的问题引入，激发学生的学习兴趣。问题引发学生两点思考:一是能不能剪;二是若能的话，则如何剪。学生一般会先从特殊三角形入手，能迅速地解决等腰三角形和直角三角形能分割，然后推广到一般三角形的问题。通过剪纸这一直观形象的实验来阐述形象的数学内容，这在教材中是很多的，如“三角形中位线定理”、“直角三角形斜边中线等于斜边的一半”及“勾股定理”等，通过这些实践操作，一方面使学生能更深入、更扎实地掌握数学知识;另一方面，也使他们的思维方式不会犯浮夸和刻板的毛病，又能准确抓住事物的本质，提出符合实际的有创新的看法。它对激发学生的创新思维有着不可低估的作用。

四、突破难点，提高课堂教学的有效性

数学知识的形成与发展，是对某些生活经验的数学化，或对学生已有数学知识的进一步数学化的过程，也就是说，新知识总是基于学生现有的知识和经验而发生、发展的。而所谓难点，是学生缺乏新知识赖以生存和发展的知识和经验，而弥补或积累途径之一可以通过学生实践活动来体验、积累。

对于教学中一些疑难点，如不借助于一定的实践活动，就不能调动学生思维的积极性，也很难达到预定的教学目标。例如:“三角形内角形和定理”的教学。在小学已获得了结论，在初中阶段进行教学时，涉及到以下问题:在哪里找到180°的角?通过什么方法把这3个角集中到一起?如何说明或证明。可以设计以下的环节:让学生将3个角剪下来;让学生按照自己的理解将3个角拼起来;引导学生探究、交流，寻找方法，可能会得到如下拼图。图1到图2是原有经验的再现，由图1到图3、图4，是在新知识背景下对原有经验的正迁移。在图3、图4中使用平行线的性质说理，是客观知识和主体思维相结合的结果，是从感性到理性的一种过渡。

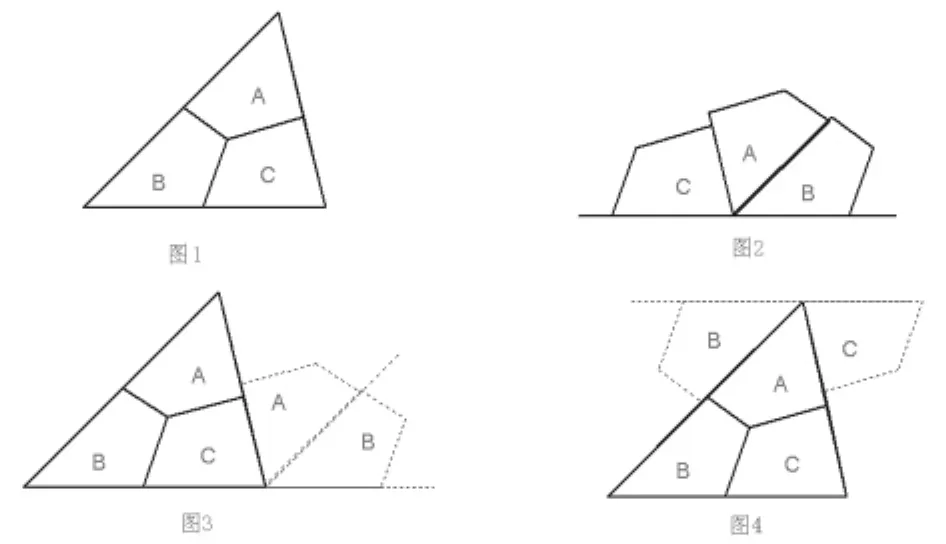
在上述活动过程中，学生获得了作辅助线的方法，上述经验的获得对学生后续知识的学习、提高数学素养是十分重要的。

五、感性到理性，呈现知识的形成过程

实践操作不仅手的操作，更注重的操作中思考;思考中操作的协同活动，有效地获得数学经验。例:“圆与圆的位置关系”教学时，组织学生运用两个不同的圆纸片作相对运动的操作，通过量一量、比一比，让学生根据自己的日常经验归纳，通过类比、归纳等思维方式，总结出两个圆的位置关系及其判定，同时对相应知识的形成过程也有了较深的了解。

六、探究交流，提升学生的自主探索和合作交流能力

《全日制义务教育课程标准》指出:数学知识不仅包括“数学事实”，即客观性知识，而且还包括属于学生自己的主观性知识，即带有鲜明个性认知特征的“数学活动经验”。其中，学生的自主探究与合作交流的能力是“数学活动经验”重要内容之一，形成于学生的自我数学活动之中。因此，数学教学应充分向学生提供实践活动的机会。把握《课标》，优化课堂设计，根据教材内容及深度特点，学生的能力情况，尽可能为学生提供实践活动的时间和空间，要着眼于学生的后续学习能力的培养。教师不能仅仅传授知识，更应引导学生自主获得知识、技能、思想、方法，以提高创新能力，即所谓“授人以鱼，不如授人以渔”。例:在要求学生解决“不过河测河宽”的问题时，学生们集思广益，结合课本知识提出了不下五种的解决方法:利用全等三角形;利用三角形或梯形中位线定理;利用等边三角形性质;利用平行四边形性质;利用相似三角形性质;利用勾股定理利用三角函数。通过这一问题解决，使学生对“不过河测河宽”所运用的相关知识有了深刻的理解。“做然后知不足”，在学生独立或合作完成实践的同时，激发了他们进一步学好数学的愿望，也促成数学教学的良性循环。

七、主动参与，培养学生应用数学的意识

强调数学与现实生活的联系现已成为各发达国家课程内容改革的共同取向，提出了“用数学于现实世界”口号。实践活动教学，可以帮助学生了解数学知识应用于现实生活中的形态，掌握常用的一些数学思想和方法，初步具备把现实生活中实际问题化为数学问题的能力。这就要求教师应努力创设一种实践的环境和空间，使学生能受到必要的教学应用的实际训练，为此，不仅要从教材中挖掘，还要从日常生活中寻找、发现数学问题。例如，初三学生每年都要参加体育中考，其中有个项目是投掷实心球，当投掷角度为多少时，球抛得最远?学校每年要举行运动会，当100m、200m、 400m、800m等跑步项目终点位置确定时，其起点位置如何确定?通过教师的指导，使学生领悟到跑道上也蕴含着丰富的数学知识。这样，通过学生的主体参与，强化了学生“问题解决”的能力，提高了学生“用数学”意识，让数学教学焕发出应有的生命活力。

智慧源于实践，实践是人们获取知识的最佳途径。但是，课堂实践活动教学方式使用，必须依据教材和学生情况而定，譬如:当学生缺乏学习新知识必须的知识经验时，才需实践活动以便积累经验，否则成课堂作秀，弄巧成拙。俗话说，教无定法，对于我们课堂教学，只有不断尝试、探索、总结、反思才会有收获和进步。

［1］刘兼等.数学课程标准.北京师范大学出版社，2002.

［2］郑毓信.从理论到实践.数学教育.上海:上海教育出版社，2001.

［3］中国数学教育，2009，(4).