对纽结的Vassiliev不变量的研究

霍承刚,王树新

（1.宿州学院数学与统计学院,安徽宿州234000;2.辽宁师范大学数学系，辽宁大连116029）

对纽结的Vassiliev不变量的研究

霍承刚,1王树新2

（1.宿州学院数学与统计学院,安徽宿州234000;2.辽宁师范大学数学系，辽宁大连116029）

介绍一类重要的纽结不变量，即Vassiliev不变量，给出了纽结Vassiliev不变量的一些性质及其作用在特殊纽结上的相关结论。

纽结；环链；Vassiliev不变量

1 引言

纽结是三维空间中的简单闭曲线，简单闭曲线意思是连通的（连成一体），封闭的（没有端点的），不自交的（自己与自己不相交，即没有粘连的）曲线。寻找拓扑不变量是拓扑学的重要议题之一，作为低维拓扑一个分支的纽结其任务亦然。1989年，V.Vassiliev和M.Goussarov各自独立的引进了有限阶纽结不变量的概念，也称为Vassiliev纽结不变量。显然，Vassiliev不变量是低维拓扑中相当新的一个概念，是基于对流形光滑映射的判别式（即带奇异点映射）研究而引入这一概念的。后来Birman和Lin给出了Vassiliev不变量的公理描述。本文采用Birman-Lin所引进的Vassiliev不变量的定义。Vassiliev不变量是一个极具特色的纽结不变量，比如它有着类似多项式的性质等。Vassiliev不变量引起了广泛的兴趣和关注，Vassiliev不变量被证明至少同琼斯多项式及其源于各种量子群的一般形式具有同等作用。像纽结的Goussarov多项式的系数，Jones多项式的导数在1的值等被证明是Vassiliev不变量，人们从不同的角度去研究刻画Vassiliev不变量的特性，例如Y.Ohyama利用纽结的相似性研究它；Ted.Stan ford利用辫交换子刻画其特点；Y.Ohyama和Harumi Yamada利用Cn-move进行研究等。近年来对其研究越来越多，相信在对纽结的分类过程中，它势必扮演比各色纽结多项式更重要的作用。[1]

本文将对纽结的Vassiliev不变量进行介绍，给出纽结Vassiliev不变量的一些性质及其在特殊纽结上的相关结论。

2 主要结果

对值域为阿贝尔群的纽结不变量，可以通过下述线束关系：

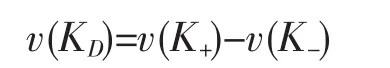
定义奇异纽结的不变量,其中KD，K+，K-表示局部，如图1。

图1

而其余部分完全相同的纽结图表。

定义1：设v为值域在阿贝尔群的纽结不变量，如果对任意多于n个奇异点的纽结有v(K)=0，则称此不变量为n阶Vassiliev不变量，通常记为vn，此定义可自然的扩充到环链上。

从不变量的定义及线束关系(1)可以得到如下事实：记Kn为有n个奇异点的纽结，则交换它的一系列交叉点而值vn(Kn)不变（其值仅由奇异点位置决定）。特别地)，其中n表示镜面像。再由vn(Kn+1)=0，这使人联想到如果f∶R→R为常值映射，则对∀x∈R有f(x)=v(-x)。

定义2[2]：设v,w为两个纽结不变量，定义它们的乘积如下：v.w(K)=v(K)w(K)。

利用归纳法易证明下面定理。

引理1[3]：令v,w为纽结J的Vassiliev不变量，K为有i个奇异点的纽结，则，其中。

此定理类似于分析上Leobniz的定理：若f,g∶Rn→R为函数，则

定理1：若v,w分别为m阶和n阶纽结不变量，则v,w为n+m阶不变量。

证明：当v,w作用于任意有n+m+1个奇异点的纽结时，由引理1可知和式中每项要么|J|＞m，要么|J|＞m.从而v(|J|)=0或w(|J|)=0，所以v,w(n+m+1)=0，Conway多项式即得证。

下面定理说明了纽结的系数与Vassiliev不变量的关系。

定理2：经过适当的变量替换，Homfly多项式的泰勒展式的系数为有限阶的。

证明：Homfly多项式的一种标准形式是以q和N为参数的多项式，且满足下列等式:

若令q=ex，然后展成x次幂形式，则上式可变形为：

上式子为关于x的“一团”的表达式，其中“一团”表示此部分比较复杂，但不管它是什么，此时多项式的系数是有限阶的。

注1：Jones多项式是Homfly多项式对N≡2的情况，所以由定理2的证明可知Jones多项式经过适当变量替换，它们泰勒展式的系数也为有限阶的。

注2：类似于定理2的证明，对Kauffman多项式也有相同结论成立。

另外，纽结的Jones多项式的阶导数在1的取值为n阶不变量。而且Jones多项式的系数不是有限阶的，但可以用有限阶不变量来逼近。[4]

引理2[5]：令{K|z∈Z}是扭转序列，若F: K→C是阶≤m的不变量，则F（Kz）是以z为变量阶≤m的多项式。

垂直扭转序列和水平扭转序列分别如图2。

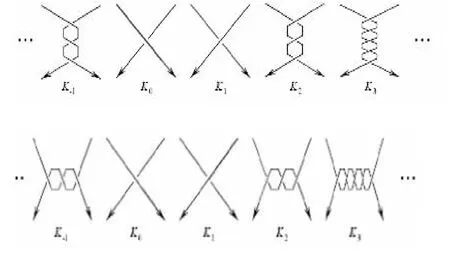
图2

定理3：纽结的不纽数不是有限阶的。

证明：考虑平凡纽结的Whitehead doubles的不纽数，

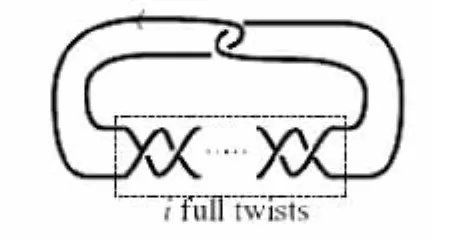
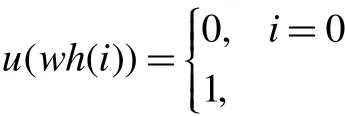
显然这不是关于i的多项式，从而不纽数不是有限阶的不变量。

对特殊纽结计算Vassiliev不变量有下面两个结论。

定理4：设Kn为有n个奇异点的纽结，由Vassiliev线束关系式去掉奇异点计算其Conway多项式，则当拆得为平凡纽结时，zn的系数为1；当拆得为分离环链时，zn的系数为0。

证明：令C(K)(z)表示纽结的Conway多项式，仍用C表示其在奇异纽结上的扩展，由Conway多项式的定义及线束关系有：

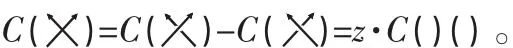
由上关系式知每去掉一个奇异点，z的次数升高一次再结合平凡纽结和分离环链的Conway多项式即得证。

下面将描述了一个关于有平凡Conway多项式的纽结当其对应的V3值（此处V3简记纽结Jones的多项式的3阶导数在1的值）满足一定条件时，它是Vassiliev值的特点。

定理5：若K为有平凡Conway多项式的纽结，则当K对应的值V3为72的倍数时，其3阶的Vassiliev值v3(K)为整数。

证明：polyak-Viro给出了不变量v3的计算公式：[6，7]

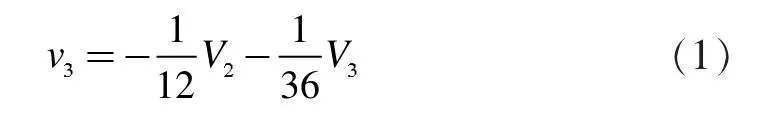
在[4]中，给出了v4的计算公式：

则当K有平凡的Conway多项式时有：

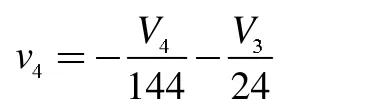
由v4的整性及事实144|V4有：

[1]D.Bar-Natan,On the Vassilliev knot invariants[J].Topology 1995,34:423-472.

[2]Y.Ohyama,Vassiliev invariants and similarity of knots,Proc.Amer.Math.Soc.1995,123:287-291.

[3]T.Stanford,Braid commutators and Vassiliev invariants[J].Pacific J.Math,1996,174:269-276.

[4]Yasutaka Nakanishi and Y.Ohyama,knots with given finite type invariants and Conway polynomial[J].Knot Theory Ramifications,2006,15(2):205-215.

[5]T.Stanford and R.Trapp,On knot invariants which are not of finite type[M].Preprint,1999：28.

[6]A.Stoimenow,On the Polyak-Viro Vassiliev invariants of degree 4[J].Canad.Math.Bull,XX(Y):1-15.

[7]J.S.Birman and X.-S.Lin,Knot polynomials and Vassiliev's invariants[J].Inventiones mathematicae,1993,111:225-270.

责任编辑：胡德明

Abstract:The paper introduces a class of important knot invariant,namely Vassiliev invariant.Some properties of Vassiliev invariant and some conclusions about its use on special knot are given.

Key words:knot;link;Vassiliev invariant

Some Vassiliev Invariants of Knot

Huo Chenggang1，Wang Shuxin2
(1.School of Mathematics and Statistics,University of Suzhou,Suzhou234000,China;2.Department of Mathematics,Liaoning Normal University,Dalian116029,China)

O189

A

1672-447X（2012）03-0001-003

2011-12-02

霍承刚（1980-），山东德州人，宿州学院数学与统计学院讲师，硕士，研究方向为低维拓扑研究。