项的代入定理

赵正波

(渭南师范学院数学与信息科学学院，陕西渭南714000)

项的代入定理

赵正波

(渭南师范学院数学与信息科学学院，陕西渭南714000)

引入两个引理分析了一阶语言中赋值的性质，简化了项的代入定理的证明，新的证明过程更能反映一阶语言的结构和等价的赋值之间的关系.

一阶语言;一阶谓词演算;项;赋值

0 引言

一阶谓词逻辑演算是比命题逻辑演算更广泛的一种逻辑系统.文献［1］对命题演算和一阶谓词演算都做了系统的论述，它们都是经典数理逻辑的重要组成部分.近年来，模糊命题逻辑得到迅速发展，文献［1］也对多值逻辑演算理论作了系统的论述，但是相应的模糊谓词逻辑的论述却比较少，我们对项的代入定理的证明进行改进，有利于我们把项的代入定理引入到模糊谓词逻辑中.另外一阶谓词本身也有许多实际应用［2－3］，文献［4］介绍了一阶模糊谓词系统的相关基本概念.

1 一阶语言的赋值与满足

下面我们先介绍一阶语言及其相关的项、合式公式、解释、赋值和满足等概念.本文中不加定义的概念参阅文献［1］.

定义1 一阶语言L含有以下符号:(i)某些变元符号:xi;(ii)某些个体常元:ai;(iii)某些谓词符号: A; (iv)某些函数符号:f;(v)连接词:¬与→;(vi)标点符号:(，)，’;(vii)量词符号:.

定义2 设L是一阶语言，则L中的项(term)定义如下:

(i)变元和L中的个体常元是项;

(iii)L中的项均由以上两种方式生成.

(i)原子公式均为合式公式;

(iii)合式公式均由以上两种方式生成.

合式公式也简称公式，L中的所有合式公式记为F(L).

定义5 设L是一阶语言，公式A(xi)是含有变元xi的公式，t是一个项.如果:

(i)xi不是A(xi)中的自由变元;

或

(ii)xi是A(xi)中的自由变元，且t中的变元在A(t)中都是自由变元，

则称t关于A(xi)中的xi是自由的.

定义6 设L是一阶语言，L的解释I的组成如下:

(i)一个非空集DI，叫解释I的论域;

(ii)DI中的一组与L中的个体常元a1，a2，…相对应的特定元

(iii)DI上的一组与L中的谓词符号 {A}相对应的关系，这里，即是DI上的n元关系;

(iv)DI上的一组与L中的函数符号 {f}相对应的函数，这里是DI上的n元函数.

一阶语言L在有了解释I之后，L中的个体常元、函数符号、项、谓词符号等就有了在DI中的明确涵义.L中的公式就成为论域DI中关于它的所有变元的一种论断，这个论断正确与否取决于所涉及的变元在DI中被怎样赋值而定，下面将给出赋值与满足的一些概念.

定义7 设L是一阶语言，I是L的一个解释.L在I中的赋值ν是从L的项集T到DI的一个映射ν: T→DI，满足条件:

(i)ν(ai)=，这里ai是L中的个体常元;

定义9 设L是一阶语言，I是L的一个解释，ν是L在I中的一个赋值，A是L中的一个公式.ν满足A可以归纳地定义如下:

(ii)若A是¬B，则ν满足A是指ν不满足B;

(iii)若A是B→C，则ν满足A是指ν满足C或ν不满足B;

2 赋值的等价关系的两个引理

引理1 设L是一阶语言，I是L的一个解释，ν，ν/，w，w/是L在I中的赋值，若

(1)t中不含xj的项(i≠j);

(2)ν/与ν是i－等价的赋值，并且ν/(xi)=v(t);

(3)w/与ν/是j－等价的;

(4)令w(xk)=w/(xk)(当k≠i，k≠j时)，w(xj)=w/(xj)，w(xi)=ν(xi)

则w与w/是i－等价的赋值，与ν是j－等价的赋值，并且w/(xi)=w(t).

证明 因为w(xk)=w/(xk)(当k≠i，k≠j时)，w(xj)=w/(xj)，所以w与w/是i－等价的赋值;

w(xk)=w/(xk)=ν/(xk)=ν(xk)(当k≠i，k≠j时)，w(xi)=ν(xi)，w与ν是j－等价的赋值;

另外，w/(xi)=ν/(xi)=ν(t)=w(t).

引理2 设L是一阶语言，I是L的一个解释，ν，ν/，w，w/是L在I中的赋值，若

(1)t中不含xj的项(i≠j);

(2)v/与ν是i－等价的，并且ν/(xi)=ν(t);

(3)w与ν是j－等价的赋值;

(4)令w/(xk)=w(xk)(当k≠i，k≠j时)，w/(xj)=w(xj)，w/(xi)=ν/(xi)

则w/与w是i－等价的赋值，与ν/是j－等价的赋值，且w/(xi)=w(t).

证明 因为w/(xk)=w(xk)(当k≠i，k≠j时)，w/(xj)=w(xj)，所以w/是与wi－等价的赋值;

w/(xk)=w(xk)=ν(xk)=ν/(xk)(当k≠i，k≠j时)，w/(xi)=ν/(xi)所以w/与ν/是j－等价的赋值;

另外，w/(xi)=ν/(xi)=ν(t)=w(t).

3 项的代入定理

定理1 设L是一阶语言，I是L的一个解释，A(xi)∈F(L)，xi是A(xi)中的自由变元.设t是关于A(xi)中的xi自由的项，ν是L在I中的赋值，ν/与v是i－等价的赋值且ν/(xi)=ν(t)，则ν满足A(t)当且仅当ν/满足A(xi).

证明 第一步，先考虑关于项中变元的代换问题.设u是L中的含xi的项，u/是在u中用t取代xi所得之项，则

事实上，我们有

(1)设u是L中的变元或个体常元，u/是在u中用t取代xi所得之项，则

ⅰ)若u=xi，则u/=t，则ν(u/)=v(t)=ν/(xi)=ν/(u);

ⅱ)若u=xj(j≠i)，则u/=u=xj，则ν(u/)=ν(xj)=ν/(xj)=ν/(u);

ⅲ)若u=ai，则u/=ai，则ν(u/)=ν(u)=

即(1)成立.

这就证明了(1)式.

第二步，回到公式中变元代换问题.先考虑原子公式.设A(xi)是A(u1，…，un)，则A(t)是A(u，…，u).设ν/满足A(xi)，即(u1，…un)在DI中成立，则由(1)式知(u，…u)在DI中成立，即ν满足A(t).

第三步，考虑一般公式变元的代换问题，用归纳法证明.

(1)设A(xi)是¬B(xi)，且定理对B(xi)已成立，则

ν/满足A(xi):当且仅当ν/不满足B(xi);

当且仅当ν不满足B(t);

当且仅当ν满足A(t).

(2)设A(xi)是B(xi)→C(xi)，且定理对B(xi)和C(xi)已成立，则

ν/满足A(xi):当且仅当ν/满足C(xi)或ν/不满足B(xi);

当且仅当ν满足C(t)或ν不满足B(t);

当且仅当ν满足A(t).

(3)设A(xi)是(xj)B(xi)(j≠i)，且定理对B(xi)已成立，因为t是关于A(xi)(即(xj)B(xi))中的xi自由的项，所以xj不在t中出现.

ⅰ)对于与ν/是j－等价的任意赋值w/，我们有赋值w如下:

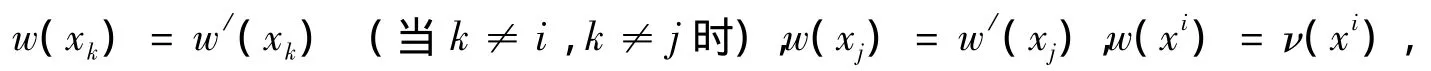
则有w与w/是i－等价的赋值，与ν是j－等价的赋值，且w/(xi)=w(t)，因而有，若ν满足A(t)，则w满足B(t)，w/满足B(xi)，ν/满足A(xi);

ⅱ)对于与ν是j－等价的任意赋值w，我们有赋值w/如下:

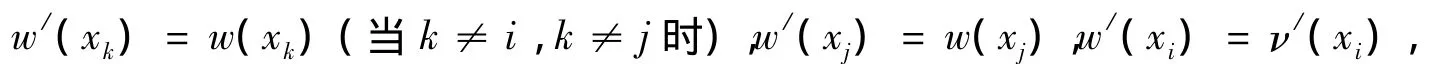
则有w/与w是i－等价的赋值，与ν/是j－等价的赋值，且w/(xi)=w(t)，因而有，若ν/满足A(xi)，则w/满足B(xi);w满足B(t);ν满足A(t).

这就证明了项的代入定理.对于项的代入定理，直接有下面推论:

推论 设L是一阶语言，I是L的一个解释，A(xi)是含有自由变元xi的公式，ν是L在I中的赋值.则

ⅱ)若ν满足A(c)，c是L中的个体常元，则ν满足公式(xi)A(xi).

4 结语

通过引理的引入改进了项的代入定理的反证法部分，证明过程更能反映一阶语言的结构，方便我们把项的代入定理引入到模糊谓词逻辑中，从而对项的代入定理的相关问题进行进一步讨论.

［1］王国俊.数理逻辑引论与归结原理［M］.第2版.北京:科学出版社，2006.

［2］赵正波.关于函数极限及其不等式性质的思考［J］.渭南师范学院学报，2004，19(5):49－52.

［3］赵正波.数列构造方法在否定命题中的应用［J］.渭南师范学院学报，2005，20(5):22－25.

［4］赵正波.模糊有效公式［J］.渭南师范学院学报，2011，26(10):54－57.

【责任编辑 牛怀岗】

On Substitution Theorem of Term

ZHAO Zheng-bo
(School of Mathematics and Information Science，Weinan Normal University，Weinan 714000，China)

The relationship of i-equivalence and j-equivalence of valuation predigests the proof of substitution theorem of term.And the proof shows structure of first-order language and the relation among valuations in first-order language.

first-order language;first-order predicate;term;valuation

book=104,ebook=77

O141.1

A

1009—5128(2012)06—0013—04

2012—02—17

赵正波(1966—)，男，陕西华县人，渭南师范学院数学与信息科学学院讲师，理学硕士.研究方向:非经典逻辑.