几个不常见的三角多倍角公式

刘小宁

（武汉软件工程职业学院 湖北 武汉：430205）

利用初等方法解决数学问题有时具有尖、深的特点［1－3］和取得意想不到的结果，文中利用复数棣莫弗定理等初等数学方法推导得到了几个不常见的三角多倍角公式，可供有关人员在教学与科研时参考。

1 三角多倍角公式

设n为正整数，则存在如下三角多倍角公式：

式（1）－（8）在有关的数学手册［4－5］及三角书籍［6］不常见。

2 引 理

为证明公式（1）－（8），先叙述2个引理。

引理1［4，6］对于正整数n，有

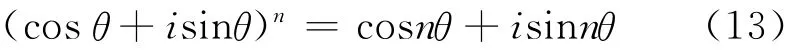
引理1是著名的复数棣莫弗（De Moivre）定理。

引理2［7］对于正整数n，有

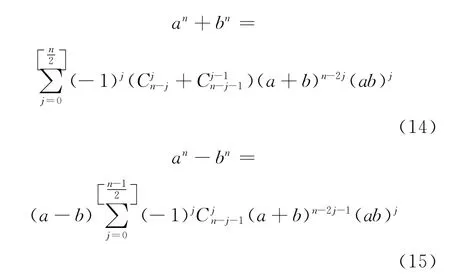
式（14）－（15）中，高斯符号［n］表示不超过n的最大整数。

引理2是二项式公式的2个等价形式［7］。

3 多倍角公式的证明

式（1）的证明：由引理2的式（14）可得

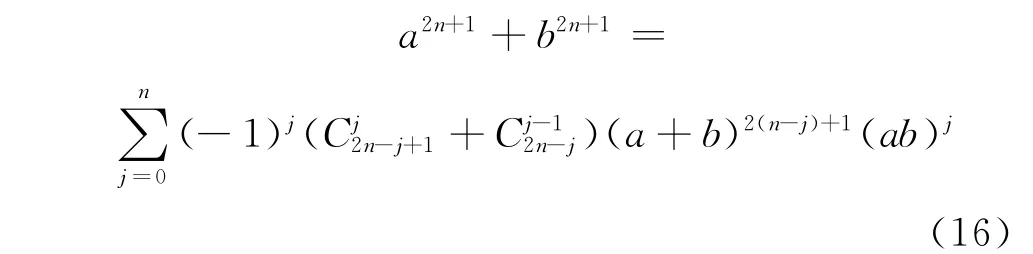
令式（16）中a＝cosθ＋isinθ，b＝－cosθ＋isinθ；由引理1可知：a2n＋1＋b2n＋1＝2isin（2n＋1）θ；因为a＋b＝2isinθ及ab＝－1，注意到i2（n－j）＋1＝i（－1）n－j，由式（16）即得式（1）。

式（2）的证明：由引理2的式（15）可得

令式（17）中a＝cosθ＋isinθ，b＝cosθ－isinθ；由引理1可知：a2n＋1－b2n＋1＝2isin（2n＋1）θ；因为a＋b＝2cosθ，a－b＝2isinθ及ab＝1，根据式（17）即得式（2）。

式（3）的证明：

令式（16）中a＝cosθ＋isinθ，b＝cosθ－isinθ；由引理1可知：a2n＋1＋b2n＋1＝2cos（2n＋1）θ；因为a＋b＝2cosθ及ab＝1，由此即得式（3）。

式（4）的证明：

令式（17）中a＝cosθ＋isinθ，b＝－cosθ＋isinθ；由引理1可知：a2n＋1－b2n＋1＝2isin（2n＋1）θ；因为a－b＝2cosθ，a＋b＝2isinθ及ab＝－1，注意到i2（n－j）＝（－1）n－j，根据式（17）即得式（4）。

式（5）的证明：由引理2的式（15）可得

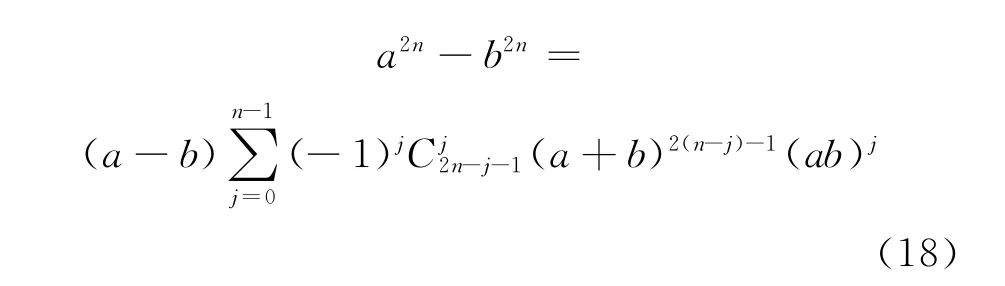
令式（18）中a＝cosθ＋isinθ，b＝－cosθ＋isinθ；由引理1可知：a2n－b2n＝2isin2nθ；因为a－b＝2cosθ，a＋b＝2isinθ及ab＝－1，注意到i2（n－j）－1＝i（－1）n－j，根据式（18）即得式（5）。

式（6）的证明：

令式（18）中a＝cosθ＋isinθ，b＝cosθ－isinθ；由引理1可知：a2n－b2n＝2isin2nθ；因为a－b＝2isinθ，a＋b＝2cosθ及ab＝1，由此即得式（6）。

式（7）的证明：由引理2的式（14）可得

令式（19）中a＝cosθ＋isinθ，b＝cosθ－isinθ；由引理1可知：a2n＋b2n＝2cos2nθ；因为a＋b＝2cosθ及ab＝1，根据式（19）即得式（7）。

式（8）的证明：

令式（19）中a＝cosθ＋isinθ，b＝－cosθ＋isinθ；由引理1可知：a2n＋b2n＝2cos2nθ；因为a＋b＝2isinθ及ab＝－1，注意到i2（n－j）＝（－1）n－j，由式（19）即得式（8）。

式（9）－（12）的简证：

把引理1利用二项式公式展开，比较其实部与虚部系数即可得到式（9）－（12）。

［1］刘小宁.用初等方法求一个无穷级数和［J］.武汉工程职业技术学院学报，2011，23（1）：79－80.

［2］刘小宁.直接计算贝努利数的新公式［J］.武汉工程职业技术学院学报，2011，23（3）：79－80.

［3］刘小宁.涉及变量个数的两个不等式［J］.武汉工程职业技术学院学报，2012，24（2）：61－62.

［4］叶其孝，沈永欢.实用数学手册（第2版）［M］.科学出版社，2006.

［5］《数学手册》编写组.数学手册［M］.高等教育出版社，1979.

［6］刘楚炤，李永银.复数与三角［M］.湖北教育出版社，1983.

［7］唐祐华.一个无名公式的问世 多个著名公式的等价［J］.湘潭大学自然科学学报，1986，（4）：1－7.