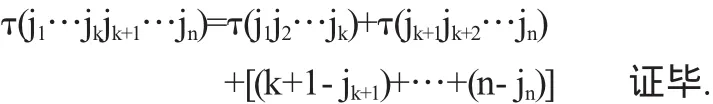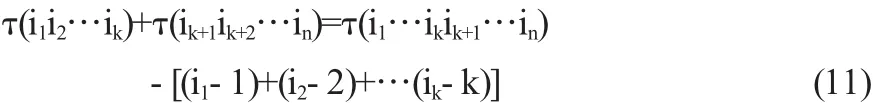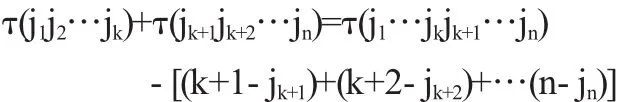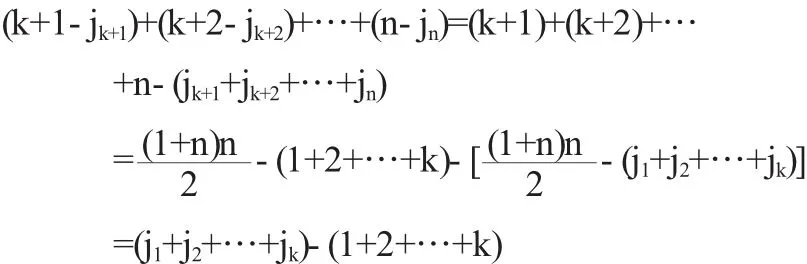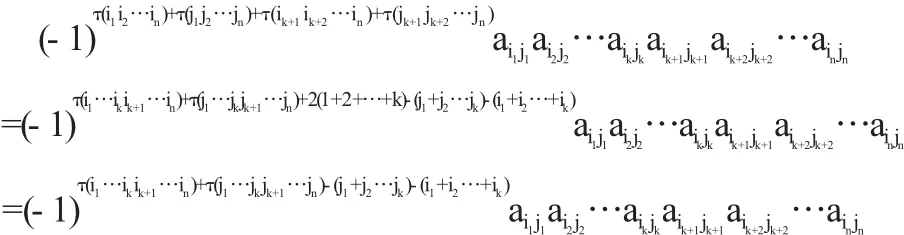拉普拉斯(Laplace)定理的新证明

殷红彩

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233000）

拉普拉斯(Laplace)定理的新证明

殷红彩

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233000）

利用排列和行列式的定义给出了行列式拉普拉斯展开定理一种简单证明,并得到了排列的两个性质.关键词：排列；行列式；拉普拉斯定理

1 拉普拉斯定理回顾

拉普拉斯定理是行列式展开的一个重要定理,该定理在理论上有重要的应用,为了叙述方便引述相关概念[1]如下:

定义1 在一个n级行列式D中任意选定k行k列(k≤n-1)，位于这些行和列的交点上的k2个元素按照原来的次序组成一个k级行列式M，称为行列式D的一个k级子式.在D中划去这k行k列后余下的元素按照原来的次序组成的n-k级行列式M'称为k级子式M的余子式.

定义2 设D的k级子式M在D中所在的行、列指标分别是i1,i2,…,ik;j1,j2,…,jk，则M的余子式M'前面加上符号(-1)(i1++i2+…+ik)+(j1+j2+…+jk)后称做M的代数余子式.

为了证明拉普拉斯定理用到了下面的引理,该引理的证明较为繁琐,在这里只叙述该引理,证明略去.

引理 行列式d的任一个子式M与它的代数余子式A的乘积中的每一项都是行列式D的展开式中的一项，而且符号也一致.

拉普拉斯定理 设在行列式D中任意取定了k(1≤k≤n-1)个行.由这k行元素所组成的一切k级子式与它们的代数余子式的乘积的和等于行列式D.

证明 设D中取定k行后得到的子式为M1,M2,…,Mt,它们的代数余子式分别为 A1,A2,…,At,定理要求证明D=M1A1+M2A2+…+MtAt根据引理,MiAi中每一项都是D中一项而且符号相同,且MiAi与MjAj(i≠j)无公共项.因此为了证明定理,只要证明等式两边项数相等就行了.显然等式左边共有n!项,为了计算右边的项数,首先来求出t.根据子式的取法知道

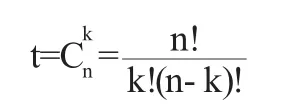
因为Mi中共有k!项,Ai中共有(n-k)!项.所以右边共有t· k!·(n-k)!=n!项.定理得证.

2 拉普拉斯定理新证明

先引入排列和行列式的定义[1]:

定义3 由1,2,…,n组成的一个有序数组称为一个n级排列.

定义4 在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序，一个排列中逆序的总数就称为这个排列的逆序数.

排列j1j2…jn的逆序数记为τ(j1j2…jn).

定义5 n级行列式

等于所有取自不同行不同列的n个元素的乘积

的代数和，这里j1j2…jn是1,2,…,n的一个排列，每一项(2)都按下面规则带有符号；当j1j2…jn是偶排列时，(2)带有正号，当j1j2…jn是奇排列时，(2)带有负号.这一定义可写成

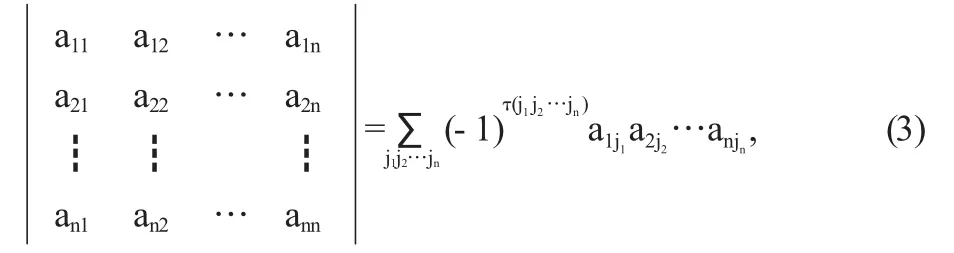
这里i1i2…in与j1j2…jk都是一个n级排列.同样可以把每一项按列指标排起来，于是定义又可以写成

为了证明引理,先给出下面两个关于排列的结论:

定理1 设i1,i2,…,ik,ik+1,ik+2,…,in是一个n级排列,若i1,i2,…,ik满足i1

证明 n级排列i1…ikik+1…in的逆序数可分为两部分:一部分是排列i1,i2,…,ik和排列ik+1,ik+2,…,in的逆序数,即分别为τ(i1i2…ik)与τ(ik+1ik+2…in);另一部分是排列i1,i2,…,ik中的数码和排列ik+1ik+2…in中的数码构成逆序产生的逆序数.注意到i1,i2,…,ik已是按顺序排列,故在排列ik+1,ik+2,…,in中,比数码i1小的数码有i1-1个.类似,在排列ik+1ik+2…in中,比数码i2小的数码有i2-2个,…,在排列ik+1ik+2…in中,比数码ik小的数码有ik-k个.故有等式

+[(i1-1)+(i2-2)+…(ik-k)] 证毕.

定理2 设j1,j2,…,jk,jk+1,jk+2,…,jn是一个n级排列,若jk+1, jk+2,…,jn满足jk+1

证明 n级排列j1,j2,…,jk,jk+1,jk+2,…,jn的逆序数可分为两部分:一部分是排列j1,j2,…,jk和排列jk+1,jk+2,…,jn的逆序数,即分别为τ(j1j2…jk)与τ(jk+1jk+2…jn);另一部分是排列j1,j2,…,jk中的数码和排列jk+1,jk+2,…,jn中的数码构成逆序产生的逆序数.注意到jk+1,jk+2,…,jn已是按顺序排列,比数码jk+1大的数码共有n-jk+1个,而jk+2,…,jn就是其中的n-(k+1)个.故剩余比jk+1大的数码的个数为(n-jk+1)-(n-(k+1))=(k+1)-jk+1,它们在在排列jk+2,…,jk中.类似,可知在在排列j1,j2,…,jk中,比数码jk+2大的数码有(k+2)-jk+2个,…,在排列j1,j2,…,jk中,比数码jn大的数码有n-jn个.故有等式

有了上面的准备,下面证明引理.

引理的证明 设D的任一个k级子式M取自的行列为i1,i2,…,ik,j1,j2,…,jk.其余子式M'取自的行列为ik+1,ik+2,…,in；jk+1,…,jn;其中i1,…,ik,ik+1,…,in与j1,…,jk,jk+1,…,jn分别为12…n的一个排列,对M按(3)式展开,其一般项为

其中i1,i2,…,ik满足i1

其中jk+1,jk+2,…,jn满足jk+1

显然,不考虑(10)式的符号,由(4)式,ai1j1ai2j2…aikjkaik+1jk+1aik+2jk+2…ainjn应是行列式(1)的展开式(4)中右边的项.下面再考察(10)式的符号,由定理1,即(6)式,得

由定理2,即(7)式,得

注意到

所以

由(11),(12)两式得

所以(10)式可化为

即行列式D的k级子式的一般项与其余子式的一般项的积是行列式D的一般项前多了符号

而这恰是行列式D的代数余子式的前带的符号,故行列式D的k级子式的一般项与其代数余子式的一般项的积是行列式D展开式中的的一般项,引理证毕.

显然用引理的新的证明方法,就文献[1]的内容安排可先在第二章的第一节给出了排列的两个新的性质,即文中的定理1和定理2,这样既分散了拉普拉斯定理证明的难度,又可使第一节的内容有了增加不再显得单薄,整个文章的安排上更为合理.

〔1〕北京大学数学系几何与代数教研室前代数小组.高等代数[M].北京:高等教育出版社，2003.

〔2〕陈志杰.高等代数与解析几何(上)[M].北京:高等教育出版社;海德堡:施普林格出版社，2000.

O151.22

A

1673-260X（2012）05-0006-02

蚌埠学院自然科学项目（2011ZR17）