常见行列式解法探析

张梦琇* 许梅兰

（[1]石河子大学理学院 新疆·石河子 832000；[2]乌鲁木齐市第八十七中 新疆·乌鲁木齐 830000）

0 前言

行列式是线性代数研究方程组的工具。求解行列式的值是解决方程组解的关键，在研究低阶行列式时，常用行列式的性质与展开式定理求解行列式的值；对于高阶的行列式，往往观察行列式的特点，根据该行列式的特点选择适当的方法，才是解决高阶行列式的关键。本文主要研究对于同一道行列式的习题，采用不同的方法求解行列式，并总结不同方法的优劣性。

1 习题解答

1.1 三阶行列式

分析：观察这个三阶行列式，会发现该行列式主对角线的元素均为，其余元素全为1，根据这个三阶行列式的特点，下面从加边法、拆分法、利用性质化简以及利用方阵特征值求解行列式的值。

解：

（1）加边法：

加边法的本质是逆用展开式定理，增加一行、一列元素使得前后两个行列式的值相等，利用行列式的性质将行列式化简成上三角行列式。其优点为：增加一行、一列元素，使得行列式的化简变得简单。

（2）拆分法：

拆分法主要是利用行列式的性质，行列式的某一行（或某一列）均是两个元素的和，这个行列式可以展开成两个行列式的和。根据行列式的特点，将行列式一分为二。其优点为：将复杂的行列式的求解过程，利用性质转成两个较简单的行列式的求解过程。

（3）利用性质进行化简：

利用行列式的性质化简行列式，主要是将行列式化成含0较多的等值行列式。这种方法适用于所有的三阶行列式的求解过程。

（4）利用矩阵的特征值求行列式的值：

利用方阵与行列式的关系，通过研究方阵的特征值，求解对应行列式的值。

1.2 n阶行列式

分析：观察这个n阶行列式，会发现该行列式主对角线的元素均为，其余元素全为1，根据这个n阶行列式的特点，下面从数学归纳法、加边法、拆分法以及特征值求解行列式的值，例题2的本质是例题1的有限推广。

（1）数学归纳法：

①当n=1时，

②当n=2时，

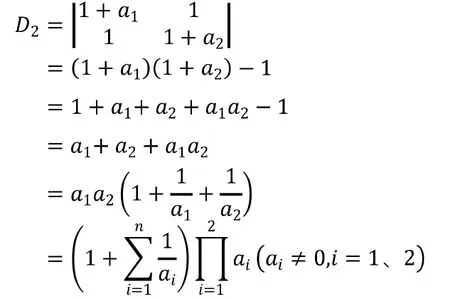
③假设当n=k时，

所以，

当n=k+1时，

所以，对于任意阶行列式D，都有上式成立。

数学归纳法一般是用在行列式值的形式与行列式的阶数有关的习题上。对于阶数别较低的行列式一般我们不采用数学归纳法。

（2）加边法：

（3）拆分法：

（4）利用方阵的特征值求解行列式的值：

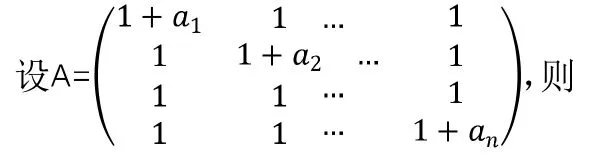
2 结论

比较这两道例题可以发现，随着行列式阶数的增加，拆分法、加边法以及方阵的特征值的方法具有普遍性，但比较发现拆分法、加边法以及方阵的特征值方法随着行列式的阶数增加，这三种方法的计算量会增大；而利用性质将行列式化简成上三角行列式不适用于高阶行列式求值问题；数学归纳法适用具有相同结构的行列式上。因此在求解行列式的值时，要先观察行列式的特点，根据行列式的特点选择适当的方法。