离散时间系统分析中初始条件的确定
赵立岭
(德州学院 物理系,山东 德州 253023)
离散时间系统分析中初始条件的确定
赵立岭
(德州学院 物理系,山东 德州 253023)
由于离散时间系统的差分方程具有迭代性,系统的全响应、零输入响应和零状态响应的初始条件可以相互转化.前向差分方程描述的系统,利用Z变换求解时,只需进行简单的初始条件替换,即可得到零输入响应的变换式.
离散时间系统;零输入响应;零状态响应;初始条件
对线性时不变系统来说,响应具有可分解性.线性时不变离散时间系统差分方程(式(1)、(2))的完全响应y(n)可分为零输入响应yzi(n)和零状态响应yzs(n)(式(3))[1-2].在时域分析中,系统完全响应、零输入响应和零状态响应表达式中的待定系数,需要根据各自初始条件进行确定.在Z变换域分析中,零输入响应也需要相应的初始条件确定.系统分析时,给定的条件往往是一组数据,可能是全响应的条件{y(n)|0≤n≤N-1},也可能是零输入响应的条件{yzi(n)|0≤n≤N-1}或{y(n)|-N≤n≤-1},还可能是零状态响应的条件{yzs(n)|0≤n≤N-1},其中N是系统的阶次.与连续时间系统的数学模型微分方程不同,离散时间系统的数学模型差分方程具有迭代性,不同响应的初始条件之间可以相互转换,这为离散时间系统地分析带来方便.

1 零输入响应的边界条件
零输入响应对应于系统激励为零时的响应,满足方程式(4).如果已知零输入响应的边界条件{yzi(n)|-N≤n≤-1},可通过式(4)迭代出零输入响应的初始条件{yzi(n)|0≤n≤N-1}.由于式(4)中激励为零,零输入响应的表达式在n<0时仍旧成立,故也可由边界条件{yzi(n)|-N≤n≤-1}直接计算零输入响应的待定系数.

对零状态响应而言,当n<0时,响应为零,由式(3)可得:

因此,零输入响应的边界条件{yzi(n)|-N≤n≤-1}也就等于全响应的边界条件{y(n)|-N≤n≤-1}.通过差分方程式(1),可以迭代出全响应的初始条件{y(n)|0≤n≤N-1},从而计算全响应中的待定系数.
由零输入响应的初始条件{yzi(n)|0≤n≤N-1}和全响应的初始条件{y(n)|0≤n≤N-1},通过式(3)可得到零状态响应的边界条件{yzs(n)|0≤n≤N-1},从而计算零状态响应表达式中的待定系数.
2 全响应的初始条件
如果已知全响应的初始条件{y(n)|0≤n≤N-1},可通过差分方程式(1)迭代出n<0的一组值{y(n)|-N≤n≤-1},由式(5)可知,该组数据就等于零输入响应的边界条件 {yzi(n)|-N≤n≤-1}.接下来,可按前述方法由{yzi(n)|-N≤n≤-1}确定零状态响应初始条件{yzs(n)|0≤n≤N-1}.
例 设离散系统差分方程为y(n)+3y(n-1)+2y(n-2)=x(n),激励x(n)=2nu(n),若(1)已知yzi(-1)=1,yzi(-2)=2,求y(0)、y(1)、yzs(0)、yzs(1);(2)已知y(0)=1,y(1)=2,求yzs(0)、yzs(1)、yzi(0)、yzi(1).
解 (1)y(-1)=yzi(-1)=1,y(-2)=yzi(-2)=2
由系统差分方程可得:y(n)=x(n)-3y(n-1)-2y(n-2)
n=0时,y(0)=x(0)-3y(-1)-2y(-2)=1-3-4=-6
n=1时,y(1)=x(1)-3y(0)-2y(-1)=2+18-2=18
同理,由方程yzi(n)+3yzi(n-1)+2yzi(n-2)=0及yzi(-1)=1、yzi(-2)=2,可迭代得出yzi(0)=-7,yzi(1)=19
则:yzs(0)=y(0)-yzi(0)=-6-(-7)=1
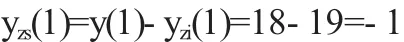
(2)由系统差分方程可得:
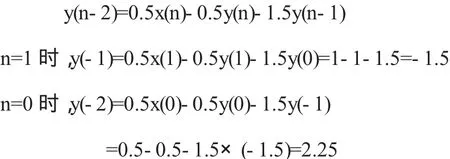
即:yzi(-1)=y(-1)=-1.5,yzi(-2)=y(-2)=2.25
分别令n=0、1,将yzi(-1)、yzi(-2)代入零输入响应方程

可得:yzi(0)=0、yzi(1)=3
则零状态响应的初始条件为:

3 前向差分方程初始条件的确定
对离散时间系统的零状态响应yzs(n)而言,n<0时,响应为零.对前向差分方程式(2)描述的系统,通过迭代可以得出,当n 也就是说,此时全响应的初始条件{y(n)|n≤N-M},就等于零输入响应的初始条件{yzi(n)|n≤N-M}.利用该结论在变换域中求解零输入响应时,会使分析变得简单. 设某离散时间系统的差分方程为: 其中x(n)=x(n)u(n),零状态响应满足yzs(n+2)+a1yzs(n+1) +a0yzs(n)=x(n),且yzs(-1)=yzs(-2)=0. 当n=-2时,yzs(0)=x(-2)-a1yzs(-1)-a0yzs(-2)=0 当n=-1时,yzs(1)=x(-1)-a1yzs(0)-a0yzs(-1)=0 从而可得:y(0)=yzi(0)、y(1)=yzi(1) 将式(7)所示差分方程进行单边Z变换并整理的: 上式右边第二项就是零输入响应的Z变换式. 当前向差分方程的N=M时,如: 将方程两边进行单边Z变换,整理可得: 式(10)右端第二项含有激励的值,是不是零输入响应呢?为此,我们分析式(9)所示系统的零状态响应方程: 把式(3)、(11)、(12),代入式(10)可得: 可见式(13)或(10)右端第二项是零输入响应. 将式(13)与式(10)、(8)相比较发现,利用Z变换求解前向差分方程的零输入响应时,只需将响应变换式中的激励初始项去掉,全响应初始值{y(n)|0≤n≤N-1}替换为零输入响应初始值{yzi(n)|0≤n≤N-1},即得到零输入响应的变换式. 综上所述,利用差分方程具有迭代性的特点,在对线性时不变离散系统进行分析时,可将全响应、零输入响应和零状态响应的初始条件进行转化,方便响应的求解.同时,在变换域分析前向差分方程所示系统零输入响应时,也可通过初始条件的转换,快速确定响应的变换式. 〔1〕吴大正.信号与线性系统分析(第4版)[M].北京:高等教育出版社,2006. 〔2〕郑君里,应启珩,杨为理.信号与系统(第二版)[M].北京:高等教育出版社,2003. O231 A 1673-260X(2012)05-0012-02 德州学院教育改革立项课题(JGLX-A09008)
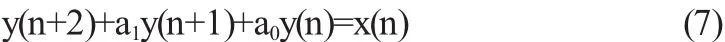


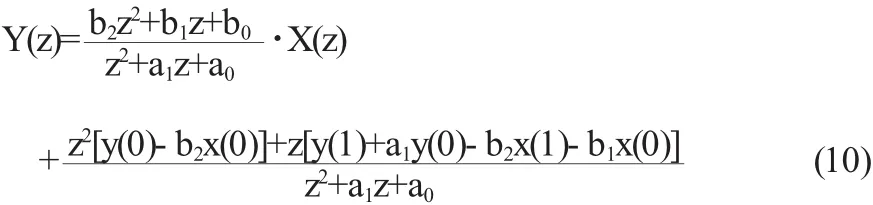

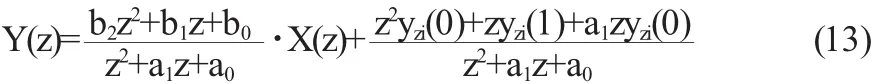
4 结论

