带Poisson跳的随机微分方程解的矩估计
崔静
(安徽师范大学 数学计算机学院,,安徽 芜湖 241000)
带Poisson跳的随机微分方程解的矩估计
崔静
(安徽师范大学 数学计算机学院,,安徽 芜湖 241000)
利用随机微分方程的基本理论及分析的技巧,研究了带Poisson跳的随机微分方程解的性质,在非线性系数满足线性增长的条件下,给出了带Poisson跳的随机微分方程解矩估计,丰富了现有文献的相关结果.
随机微分方程;Poisson跳;Ito公式;P-阶矩
众所周知,随机微分方程理论在系统与控制科学、金融学、经济学等诸多领域有着广泛的应用[1,2].近年来,带Poisson噪声的随机微分方程引起了许多学者的广泛关注,许多精美的结果参见文献[1-5].本文在现有结果的基础上,利用Ito公式、Burkholder不等式及分析的技巧,研究了带Poisson跳的随机微分方程解的性质,在非线性系数满足线性增长条件下,给出了带Poisson跳的随机微分方程解的矩估计,丰富了现有文献的结论.
1 预备知识
令|·|表示R上的欧几里得范数,R+=(0,∞)令(Ω,F,{Ft}t≥0, P)是一个完备的概率空间且满足通常的条件,即{Ft}t≥0是单增、右连续的σ-族且F0包含所有的P-零集,B={Bt}t≥0是定义在(Ω,F,{Ft}t≥0,P)上的标准的一维布朗运动.N(ds,dy)是(R+× U,B(R+)×A)上的特征测度为v(dy,ds)的Poisson随机测度且与B={Bt}t≥0独立,其补偿随机测度为N(ds,dy).考虑如下带Poisson跳的随机微分方程

其初始条件为x(0)=x0∈R对T>0假设b,σ:[0,T]×R→R, h:R×R→R为Borel可测的函数.
众所周知,当非线性系数b,σ,h满足相应的Lipschitz条件和线性增长条件时,方程(1.1)存在唯一的强解,以下若无特别说明,总假设方程(1.1)存在唯一的强解.为了研究方程(1.1)解的p-阶矩,需要作如下假设:
(H1)对q>2存在一个正常数 使得
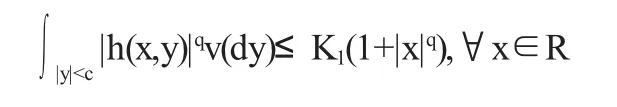
(H2)对所有的t∈[0,T]及y∈R存在一个正常数K2使得

2 主要结果及证明
引理2.1[2]若x(t)是方程(1.1)的解,则对p≥2,存在常数cp>0,使得对所有的t≥t0>0,都有

引理2.2[3]对任意p≥2,若,则
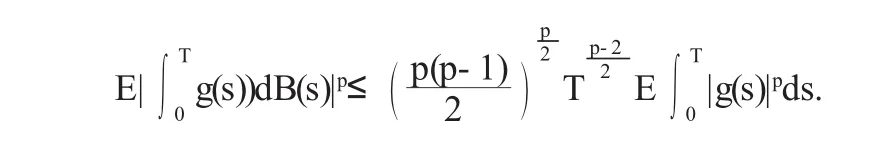
定理2.1 令x是方程唯一的解.若假设成立,则存在一对正常数c1,c2使得对p≥2及t∈[0,T]有

其中

c0=K2p(p-1),c(p,T)是一个仅依赖于p,T的正常数.证明 由(H2)可得

对t∈[0,T],由Ito公式可得,

利用(2.1)及(H2)进一步计算可得

从而可得

其中
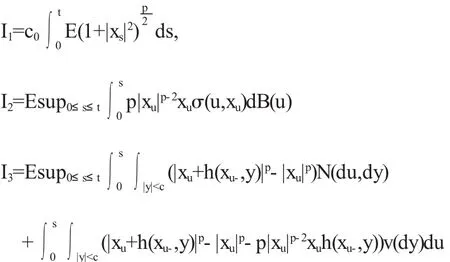
下面估计上述的Ii,i=1,2,3.易知,

由Burkholder-Davis-Gundy不等式、Holder不等式及(H2)可得


注意到由Ito公式可知

进而,由引理2.1及(H1)可得

由上述估计计算可得

由Gronwall不等式知定理得证.
定理2.2 在定理2.1的条件下,存在正常数ci,i=3,4,5使得对所有的p≥2,0≤s≤t≤T都有
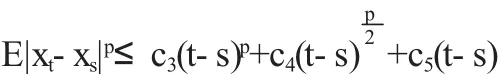
证明 运用Holder不等式及一个基本的不等式|a+b+c|p≤3p-1(|a|p+|b|p+|c|p)可得

由引理2.2,类似于定理2.1中I3的推导我们有
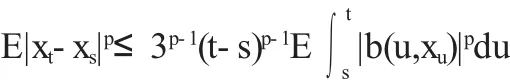

由(H1)及(H2)计算整理可得
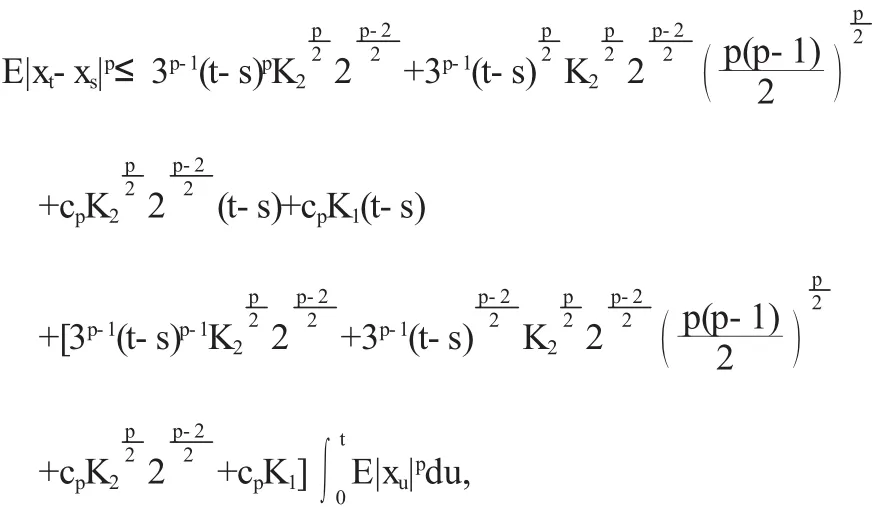
由定理4.1易知

其中
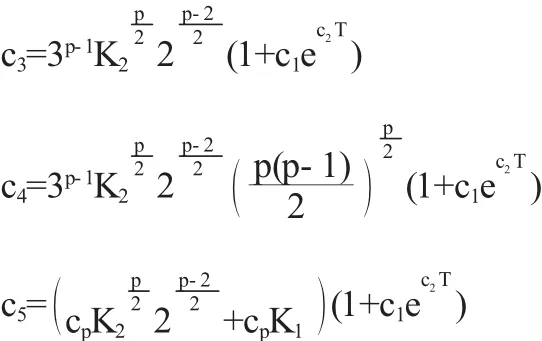
定理得证.
〔1〕D.Applebaum,Levy Processes and Stochastic Calculus. Cambridge University Press,2004.
〔2〕H.Kunita,Stochastic diffential equations based on Levy processes and stochastic flows of diffeomorphisms.Real and Stochastic Analysis,New Perspectives,M.M.Rao., 1984.
〔3〕X. Mao, Stochastic Differential Equations and Applications[M].Horwood,1997.
〔4〕M.Siakalli,Stability propertiesofstochastic diffential equations driven by Levy noise.University of Sheffield PhD thesis,2009.
〔5〕T. Yamada, On the successive approximation of solutionsofstochastic differentialequations.J.Math. Kyoto Univ.21,(1981)501-515.
O211.9
A
1673-260X(2012)05-0003-03
安徽省教育厅自然科学基金(KJ2011z147)

