在线测试系统中自动组卷数学模式的分析和建立

卢妙娜，王 润

（1.韩山师范学院 外语系，广东 潮州 521041；2.汕头大学 法学院，广东 汕头 515800）

在线测试系统中自动组卷数学模式的分析和建立

卢妙娜1，王 润2

（1.韩山师范学院 外语系，广东 潮州 521041；2.汕头大学 法学院，广东 汕头 515800）

随着教学的深入改革，传统的考试模式已经不能很好地适应改革的形势，在计算机技术迅速发展的时代，在线测试系统应运而生.试卷是由一道道试题组成的，那么在测试系统里，试题是存放在试题库里的，所以试题库结构的设计显得十分重要.在线测试系统通过一定的智能算法，在满足组卷的各种约束要求的前提下，从试题库中自动挑选出合适的试题，组成适合考核的试卷，把传统组卷过程中的多个环节缩小，不但提高工作效率，节约大量的人力、物力，而且实现了考教分离，大幅度提高考试成绩的客观性和公正性，提高考试的质量，克服传统考试的弊端.

在线测试；自动组卷；试题质量；数学模式；教学改革；考试模式

1 前言

随着教学的深入改革，传统的考试模式已经不能很好地适应改革的形势，在计算机技术迅速发展的时代，在线测试系统应运而生.在线测试系统通过一定的智能算法，在满足组卷的各种约束要求的前提下，从试题库中自动挑选出合适的试题，组成适合考核的试卷，把传统组卷过程中的多个环节缩小，不但提高工作效率，节约大量的人力、物力，而且实现了考教分离，能够确保考试成绩的客观性和公正性.要提高考试质量必须把握好组卷这个核心环节.组卷是否科学，关键在于试题是否有反映性和合理性.那么，如何设计和建立合理科学地试题库呢？下面将从自动组卷时必须遵循的基本原则、各类试卷的指标体系及关系、如何建立成卷模式，并进一步建立组卷问题的模型等方面进行分析.

2 遵循的基本原则

众所周知，试卷是用来考察学生对所学知识能否熟练运用；同时也是教师教学成效的检验，达到改进教学方法的目的.也就是说，通过试卷来考察学生学到什么，会做什么，因此属于目标参照性测验.

从这个角度出发，组卷应遵循下面几个基本原则：

（1）用户能够组合指标相同而考试内容不同的试卷.考试内容繁多，如何提高组卷的高效率，则必须从类型化方面入手，确保分类的合理与便于统计.可以多设计几套预案试卷，出题者预先自我测试，以选择最合理的用于学生检测.

（2）考试内容，试卷的各章节所占的分数比例都可以由用户决定.考试内容作为试卷的主体部分，必须能够保持合理的比例与章节分配，这样的试卷检测才会有主有次，能够突出重点学习内容.

（3）试题的难易程度要适中，要在考试大纲的范围内，要符合不同考试者和考试时间.试题的设置不能过难或者过于简单，应该在照顾学生学习水平的基础上，检测学生的实际学习能力，太难则会打击学生的积极性，太容易反而影响学生的进取心.

（4）考察的知识点要全面，在各个章节的分布要合理，能充分反映考试内容.学生在一段时间的学习之后，掌握了大量的知识点，在组卷的时候一定要全面覆盖这些知识点，以保证能够全面地检测学生的学习能力.

（5）试卷要有一定的区分度，分辨出学生不同水平和能力差异，才能达到测试的目的，避免考生的分数趋于一致.学生的水平良莠不齐，如果试卷过于简单或者复杂，没有一定的区分度，分数就容易“扎堆”出现，不适于用于检测，只有试卷有难有易，才能全面检测.

（6）选题要科学，题目类型所占比例因需要可以作调整.选题作为组卷的关键环节，一定要注意搭配、科学，各种类型的题目都要设计，并且根据题目类型的不同，来确定题目的数量和分数比值.

3 指标体系

大家都知道，试卷是由一道道试题组成的，那么在测试系统里，试题是存放在试题库里的，所以试题库结构的设计显得十分重要.由于试题本身含有固定的属性，这些属性指标不仅真实地体现其内在特征、外部属性，而且还体现出它在试卷中的比例，是选题组卷的根本，直接关系到组卷的科学性和时间.

通常，试题属性指标主要有题号、题型、考点、难度、分值、时间、区分度等.其中，难度、区分度都是十分重要的属性，但不是试题的固定属性.它们的确定有相当的难度，原因在于它们是通过考生的成绩而反映的特性，是与某批考生有关，会根据对象的不同而有所改变.因此，在建立试题库的时候，需要给试题的难度和区分度设置一个初始值，再根据每批考生的测试成绩，按某种算法进行更正和改进.

4 成卷模式

组卷是根据用户需求或预定规则，在测试系统的试题库中挑选合适的试题组合成试卷的过程，这个自动组卷的过程实际上是分值组成的矩阵分布.我们将每个矩阵看作是需要实现的约束条件.

4.1 考点与分值约束

考点与分值约束是指对每个章节在试卷中的比例，甚至是各章节的知识点能确定组成试题的比例进行约束，这样才能使试卷科学合理检测出学习成效.

由于考试科目的各章节分值不同，假如一份试卷，章节用Z代表，对于一套试卷T=(T1,T2,…,Tm)而言，m为试卷T总题数，Tj为第j道试题，m(j)为试题Tj的分数，c(j)为试题Tj所在章节.设zi为试卷的第i章节的分数，n为章节数，则考点-分值约束为：

其中，

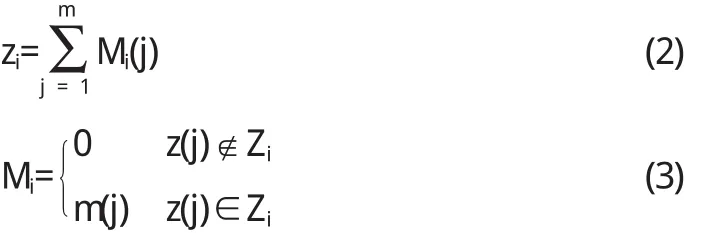
4.2 题型—分值约束

题型约束是指对试卷中各种类型的试题所占的比例进行约束，用T T表示试题类型，设题型—分值约束为：

与考点—分值相似.

4.3 难度—分值约束

对一套试卷T=(T1,T2,…,Tm)而言，m为试卷T总的题数，Tj为第j道试题，m(j)为试题Tj的分数，T D(j)为试题Tj的难度级别.用T D表示难度，设t di为试卷的第i个难度级别的分数，n为难度级别的个数，则难度-分值约束为：

其中

如果难度级别划分为三个等级，则T D={易，中，难}，那么n=3.

4.4 总分

设试卷期望总分数为M0，实际组成试卷T的总分数为M0(X).则

其中，m为试卷T的总题数，mj(X)为试卷T的第j道题的分值.

4.5 偏差计算

分别用N D，Z，T T，M分别表示难度、考点、题型、总分数的期望值，用N D(T)、Z(T)、T T(T)、M(T)表示对试卷T的预估计值，偏差分别表示为e r r o r(N D,T)、e r r o r(Z,T)、e r r o r(T T,T)、e r r o r (M,T)，则偏差越小T越接近期望值，所以：

4.6 目标函数

组卷的目标是从试题库I=(T1,T2,…,Tn)中，寻找一个子集T=(T1,T2,…,Tm)，使得这个子集T满足上面所描述的成卷模式中的各个约束分布.其中n是试题库的试题数总量，m是一套试卷的试题数总量.

假设试卷中每一道试题，都包含有题号、题型-分值、难度-分值、考点-分值的四维向量(a1,a2,a3,a4)，则一份拥有m道试题的试卷，就决定了唯一的m 4的矩阵S：

考虑到测试的合理性，防止试题的重复出现，我们要设置一个约束来控制试题出现重复的概率，因此，需要增加一个约束条件来控制重复率.设试卷T中任意试题T上一次在试卷C F1(X)中出现，本次组卷中试卷C F2(X).则对重复率的要求可以表示为：

这个约束条件和目标函数就是建立的实现成卷算法的数学模型.

5 结论

自动组卷问题在在线测试系统中是一项非常复杂的数学模型问题，首先组卷者要熟知大纲和命题的要求，了解考试类型、对象和目的；明确题型和题量.其次要科学组合题目，并附加详细试题答案.按照试题主要属性各个指标的约束分数得出组卷的目标函数，结合控制试题重复率的约束条件，最终实现成卷算法的数学模型.

〔1〕戴亚非，李晓明.计算机自动组卷算法分析[J].小型微型计算机系统，2005，16（9）：51-55.

〔2〕宋兆鸿，刘世表，张才美.现代教育测量[M].北京：教育科学出版社，1986.

〔3〕卢开澄.组合数学[M].北京：清华大学出版社，2001.10-100

〔4〕于志敏.刘延华.选题组卷策略研究[J].电脑开发与应用，2001，14（3）：32.

〔5〕刘方爱.一种通用试题库模型及试卷生成算法[J].计算机应用与软件，2008，15（4）：52-56.

T P 311.52

A

1673-260 X（2012）09-0039-02