同余理论在单循环比赛中的应用

李 文，邹 都

（平顶山学院 数学与信息科学学院，河南 平顶山 467000）

同余理论在单循环比赛中的应用

李 文，邹 都

（平顶山学院 数学与信息科学学院，河南 平顶山 467000）

在文献[4]给出的单循环比赛赛程编排方法的基础上，为了使比赛更具观赏性，利用同余理论对单循环比赛的赛程编排方法进行改进，并给出了具体证明.

同余理论；单循环比赛；赛程编排

单循环比赛的赛程编排存在着多种方法，比如“贝格尔编排法[1]”、“固定1逆时针轮转法[2]”、“蛇形编排法[3]”等等.文献[4]给出运用同余理论的相关知识来编排n支队进行单循环比赛赛程的一种方法（具体赛程编排方法请参看文献[4]第8章的内容）.

例1 利用文献[4]给出的单循环比赛的赛程编排方法求有7个球队进行单循环比赛的程序表.

解 此时n=7为奇数，增加一个编号为8的队，凡是与第8队比赛的队即为轮空.循环比赛安排程序表如表1：

表1 n=7

文献[4]给出的单循环比赛赛程编排的算法，能够实现计算机对其的操作，在实际中有很强的可运用性，但是在某些情况下它又存在着相应的不足之处.以表1为例，不难发现上述编排方法的缺陷：(1)当比赛的球队编号是按各队的实力强弱及上年比赛的成绩好坏而编排时，上述编排法确实存在着明显的弊端：1、2号队在第三轮比赛中相逢，使比赛的高潮过早出现，不能为全场比赛起到压轴作用，这显然不符合观众观赏的需要，影响整个比赛的观赏性.(2)当参赛队数为奇数时，在实力相当且最强的两队1、2相遇之前，1号队经历了两场比赛且第一场是与最弱队比、第二场比赛又是轮空，这对2号队显然很不公平，使其能“黑马”出现的希望变得更加渺茫.针对上述编排法存在的这两点不足，我们试着对其进行某些方面的改进，使其既保持了上述编排方法的优点又能弥补一下它的不足，进而使得整个比赛更加完美和合理.

若参赛队n为奇数时，我们把一个“假想的”队A加到这n个球队中，就有了n+1球队.现在，在每一轮比赛中对这n+1个球队进行安排，并且规定：凡被安排与队A比赛的球队就是轮空的球队.这样，n为奇数的情形即可转化为n为偶数的情形.因此，在下面的讨论中总假设n为偶数.

下面用同余理论给出改进后的n支队进行单循环比赛的赛程编排方法，并证明只进行n-1轮比赛即可.

用i(1≤i≤n-1)来表示轮次，用xi(1≤i≤n-1)表示第i轮比赛中与队x进行比赛的队，则要给出所要求的单循环比赛的程序表时，只须确定出第i(1≤i≤n-1)轮比赛中与队x比赛的队xi，且xi满足下列的两点要求：

(i)当x≠n且

时，取xi满足

(i i)当x=n时，取

显然n≠ni.

证明 首先指出，在每一轮比赛中，不同球队的比赛对手是不同的，即若x≠x'，则xi≠xi'(1≤i≤n-1)，分以下三种情况进行讨论：

(a)若x与x'都不等于n，且x,x'都满足式(1)时，xi与xi'由式(2)确定，由于1≤x,x'≤n-1，于是x-x'堍0(m o d n-1).由式(2)得

于是

因此得xi≠xi'.

(b)若x=n，x'=ni则xi=ni,xi'=n，显然xi≠xi'.

(c)若x=n，但x'满足(1)，则xi'可由式(2)定义，此时，如果xi=xi'=ni，那么由式(2)和(4)知，当i是偶数时，有

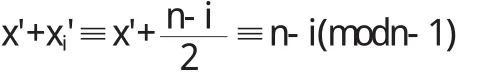
故

当i是奇数时，有

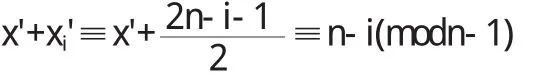
但是，根据对x'的假定，式(5)和式(6)都不能成立，因此xi≠xi'(1≤i≤n-1).

其次指出，每一个队x在每一轮比赛中的对手都不是他自身，即对于1≤i≤n-1，必定x≠xi.事实上，当x=n时，由式(3)可知n≠ni；当1≤i≤n-1且式(1)满足时，若x=xi，则由式(2)给出2 x≡x+xi≡n-i(m o d n-1).再根据一次同余式有解的充要条件和(2,n-1)=1可知：2 x≡n-i(m o d n-1)，在1≤x≤n-1内有且仅有一解.从而说明x≠xi.

最后指出，对于每一个确定的队，它在各轮比赛中的对手是不同的，即当i1≠i2时必有xi1≠xi2(1≤i1,i2≤n-1)，分两种情况讨论：

①先看球队n，如果

由式(3)可知，

因此i1=i2.

②再看球队x(1≤x≤n-1)，如果xi1=xi2=n，则ni1=ni2(1≤i1, i2≤n-1)，因此由①中的讨论可知i1=i2；如果xi1=xi2≠n，那么由式(2)得到

因此i1=i2.

以上讨论说明，用上面的方法可以在n-1轮比赛中完

故成n个球队的循环比赛.

例2 用“改进后的单循环赛的编排方法”求有7个球队进行单循环比赛的程序表.

解 此时n=7为奇数，增加一个编号为8的队，凡是与第8队比赛的队即为轮空.循环比赛安排程序表如表2：

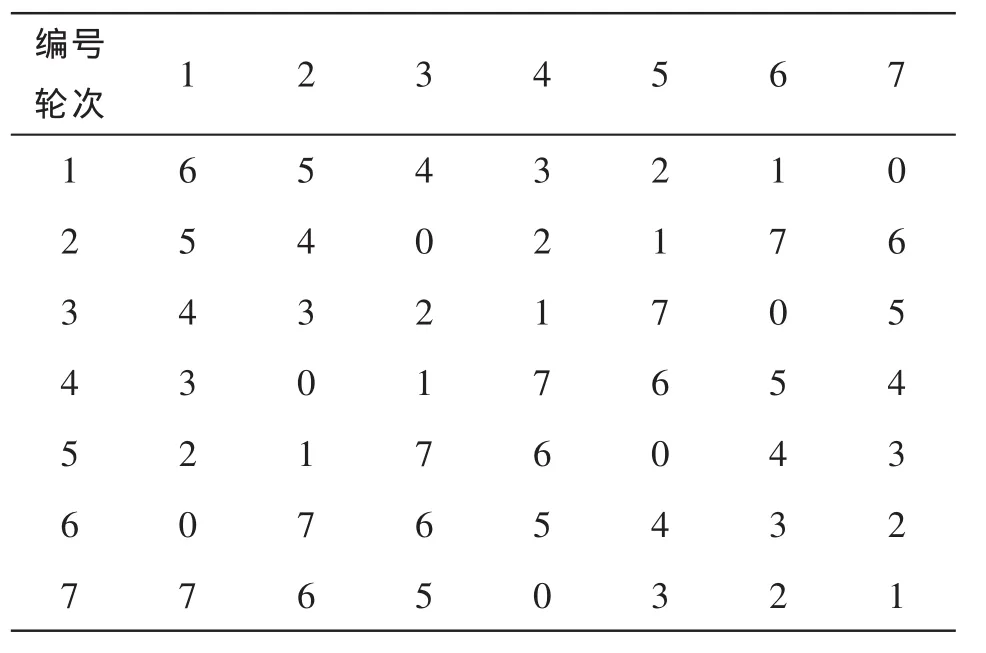
表2 n=7

通过比较改进前后的两种单循环赛的编排方法及表1、表2我们可以看出，改进后的编排方法不仅能够保留改进前的编排方法的优点：便于实现计算机对其的操作，而且改进后的编排方法确实在一定程度上能够避免改进前的编排方法中存在的一些不足.下面就以表1、表2为例来具体分析一下，从表1与表2的对比我们可以清晰的看到：(1)在第一轮中，实力相当的3、4队相逢，可以作为开幕式的开幕战，能够吸引观众，提高观众的看赛热情.(2)全赛的高潮放在了最后面的的三轮上，使比赛进行的波澜起伏.(3)表2中不仅对1、2队相当公平，而且对6、7号队也是比较公平的，尤其是对2队和7队的出线能够创造更大的可能性，使比赛进行的更加激烈，可观赏性更强.由表1、表2相比的优缺点可以看出：改进后的单循环比赛的赛程编排方法不仅有利于“黑马队”的出现，使其取得的成绩和平时的付出成正比，而且1、2号队在比赛的倒数第三轮相遇，使比赛的高潮在适当的时候出现，可以提高观众的看赛热情，使比赛更具观赏性.

〔1〕董东风，肖波.论循环赛“贝格尔编排法”[J].长沙通信职业技术学院学报，2010，9(3):92-95.

〔2〕傅企明，赵成，刘继领.增强循环制编排合理性的探索[J].中国体育科技，2007，43(2)：136-143.

〔3〕董东风，宋小春.循环赛中倒轮次编排方法的研究[J].长沙通信职业技术学院学报，2007，6(1)：93-96.

〔4〕王丹华,杨海文,刘咏梅.初等数论[M].北京:北京航空航天大学出版社,2008.

O 12-49

A

1673-260 X（2012）09-0003-02

平顶山学院校级教研项目（2010-YJ14）