基于固定宽度直方图的分布估计算法的一种改进

刘建军，韩 帅，石定元，武国宁

（中国石油大学理学院，北京 1 0 2 2 4 9）

基于固定宽度直方图的分布估计算法的一种改进

刘建军，韩 帅，石定元，武国宁

（中国石油大学理学院，北京 1 0 2 2 4 9）

基于固定宽度直方图分布的分布估计算法（F WH），提出一个改进方案，即在F WH算法中加入概率阈值的要素，不使用改变区间长度的更新方式，保证区间个数不增加，并在更新候选解步骤中加入模式搜索法（H o o k e-J e e v e s方法），构造出一种改进的优化算法（H J-F WH）。数值实验结果表明，改进后的算法在最优解精度和收敛速度方面均有了较大的提高。

分布估计算法；模式搜索法；直方图；概率模型

分布估计算法（E D A s:E s t i m a t i o n o f D i s t r i b u t i o n A lg o r i t h m s）是进化计算领域新近兴起的一类随机优化算法，它将传统的遗传算法的思想和统计学的概率模型结合起来，形成一种全新的智能优化计算模式。

分布估计算法可以按照概率模型的复杂程度进行分类，包括变量无关的P B I L、U M D A和c G A算法；双变量相关的M I M I C、B M D A算法以及多变量相关的E CG A、F D A、B O A等算法。美国卡耐基梅隆大学的B a l u j a在1 9 9 4年提出P B I L算法，是用来解决二进制编码的优化问题，虽然当时还没有提出分布估计算法的概念，但是P B I L算法被公认为最早的分布估计算法模型。

直到1 9 9 6年,分布估计算法的概念才第一次提出。其中U M D A算法由德国学者M u h l e n b e i n于同年提出，它与其他算法不同在于其概率向量的更新方式。之后的M I M I C算法，是由美国M I T人工智能实验室的D e B o n e t等人于1 9 9 7年提出的一种启发式优化算法，此算法是最先考虑两个变量相关。而B O A算法是由美国U I U C大学的P e l i k a n等提出的，此算法主要研究多变量相关的问题。

该文选取基于固定宽度的直方图模型的分布估计算法（F WH算法）为基本方法，加入概率阈值的要素，防止函数早熟，同时考虑到算法效率，而不使用改变区间长度的更新方式，保证区间个数不增加，可以加快迭代速度，并在更新种群步骤中加入模式搜索法（H o o k e-J e e v e s方法），可以有效地提高逼近解的精度。

一、基于直方图的分布估计算法

（一）基本介绍

基于直方图的分布估计算法的模型一般分为两种，一种是区间宽度固定的直方图模型F WH(t h e f i x e d-w i d t h h i s t o g r a m)，另一种是区间高度固定的直方图模型F H H(t h e f i x e d-h e i g h t h i s t o g r a m)。其中，F WH将变量的定义域划分为宽度相同而高度不同的小块区间，小块的高度决定了该范围取值的概率大小。而F H H则将变量的定义域划分为宽度不同而高度相同的小块区间，小块的宽度代表了该小块取值的概率大小。同基于高斯分布的分布估计算法相比较，F WH和F H H使用了更加简单的均匀分布概率模型，而且通过控制每个小块的宽度或高度，能够有效地求得相对精度较高的结果。由于F WH和F H H都在优化连续问题时得到结果精度的大小，基本取决于在定义范围内各维小区间划分的个数，所以，既要保证小区间分得要细，算法迭代速度也不能太慢。该文考虑变区间算法的计算复杂性较高，故选取F WH算法作为基本算法来改进。

（二）F WH算法步骤：

S t e p 1初始化候选解，给定初始参数。

S t e p 2构造初始概率模型，现将变量的每一维进行等分，保证每个小区间初始概率相等。

S t e p 3通过随机方式构造初始候选解，保证各点均匀分布在各个小区间上。

S t e p 4计算候选解的适应值，根据各点适应值，选择所要的优势候选解。

S t e p 5更新概率向量，根据优势候选解的变量所在区间，用更新公式更新每个小区间概率向量。

S t e p 6达到给定迭代次数，输出结果。

二、基于模式搜索法的固定宽度的直方图分布估计算法（H J-F WH）

（一）模式搜索法

模式搜索法的基本思想，从几何意义上讲，是寻找具有较小函数值的低谷，试图通过迭代产生序列沿山谷向极小点逼近。算法首先从初始点开始进行两种类型的移动，即探测移动和模式移动。探测移动是依次沿个坐标轴进行，用来确定新的基点和有利于函数值下降的方向。模式移动是沿相邻两个基点连线方向进行，试图沿着山谷方向使函数值更快地减小。

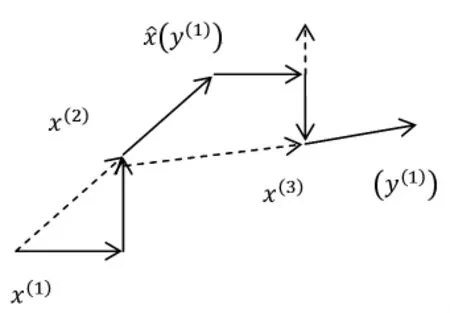
图1 模式搜索法示意图

（二）结合模式搜索法的直方图分布估计算法

在模式搜索法结合直方图分布估计算法（H J-F WH）中，在更新种群步骤中应用模式搜索的思想，先对种群的每一维进行探测移动，完成后再进行模式移动，找到新的基点，若无效则退回原基点，按照初始步长γ及缩减率β更新步长，再从这个基点出发，依次沿各坐标轴方向进行探测移动。如此继续下去，直到满足精度要求，即步长δ小于事先给定的某个小的正数ε为止。

在H J-F WH算法中的概率阈值按以下方式更新：当某一个小区间概率大于阈值时，对需要更新的变量区间的概率变为原来的，其他的每个区间的概率加上这个区间概率的。即第i个小区间的概率Pi≥G，则将这个区间的概率变为，其他区间的概率变成，（k=1，2…，i-1，i+1…，N）保证每一维小区间概率和为1。H J-F WH算法步骤：

S t e p 1初始化：对参数如候选解规模M、细分等分数N、优秀候选解规模δ（δ＜M）、概率阈值G、学习概率α、迭代次数Gen等给定初值。

S t e p 2构造概率模型：需要先对变量的连续空间进行等分。例如某一维的变量的连续空间为[a，b]，如果进行N等分，则每一份区间的长度是。因为是进行N等分，所以开始这N个区间的取值概率都是相同的，也就是对于每个变量的连续空间，进行了N等分以后，每个小区间取值的概率都是。

S t e p 3构造新解：即对每个个体的每一维变量进行赋值。一般通过产生随机数采用轮盘赌的方式确定每个变量的取值。

S t e p 4确定新的优秀候选解：计算候选解的适应值，根据其适应值，对候选解进行排序，选择前δ个适应值较好的解作为优秀候选解δ（k）。

S t e p 5模式搜索法更新当前最优解：将这前δ个适应值较好的解中最好的一个解采用模式搜索算法，得到一个新的最优解，完成更新。

S t e p 6更新概率向量：对于变量某一维取值的连续空间，在它的N个划分小区间里，统计含有优秀候选解的个数，设某个小区间中含有优秀候选解的个数为ni，更新前该小区间的概率为pi，则更新后的概率为。

S t e p 7判断概率是否超过阈值：当某个小区间的概率大于G，则将区间概率进行重新更新，否则不需要更新。

S t e p 8算法停止条件：当算法进行了一定数量的迭代次数后，算法停止，并输出结果。

三、数值实验

（一）实验对象及参数设置

选取三个连续优化问题的经典函数作为测试函数进行数值实验，实验中候选解规模M=1 0 0 0，优秀候选解规模δ=1 5 0，区间细分等分数 N=1 5 0，学习概率α=0.5，概率阈值 G=0.8，最大迭代次数Gen=2 0 0，初始步长γ=0.5，加速因子λ=1，缩减率β=0.5。

表1给出了三个函数的表达式、定义范围及维数、最优解和最优值，表2列出了F WH算法与H J-F WH算法针对各函数的数值实验比较结果。

表1 测试函数

表2 结果对比（2 0次实验结果的平均水平）

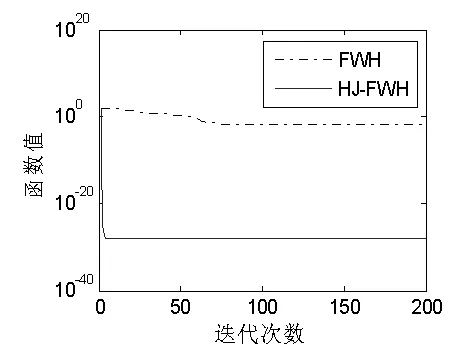
图2 F WH与H J-F WH对f1的收敛图

图3 F WH与H J-F WH对f3的收敛图

图4 F WH与H J-F WH对f3的收敛图

通过上面的图表可以明显看出，改进后的H J-F WH算法的最优解精度有大幅的提高，而且比起F WH算法逼近最优解的收敛速度要快，改进效果比较明显。

（二）参数调整

一般来说，参数的选取对算法的性能影响很大，下面对H J-F WH算法中的参数进行数值比较，这里采用控制变量法，即每次只改变一个变量。表3、表4、表5和表6分别只列出了在H J-F WH算法中解的取值区间细分等分数N、优秀候选解规模、概率阈值G和允许误差分别对算法获得最优值的影响。

表3 区间细分等分数N

表4 优秀候选解规模δ

表5 概率阈值G

表6 允许误差ε

对于H J-F WH算法，通过以上参数调整的实验结果表明，只有允许误差的影响对于解的精度影响较大，即ε越小解精度越高，而其他参数对于解的精度影响较小。而对于F WH算法区间细分等分数N、优秀候选解规模δ、概率阈值G等参数对于解的精度相对来说影响较大，尤其是细分等分数N，这里不做详述。

通过上述几组数值实验结果表明，改进后的H J-F WH算法比起改进前在解的精度和收敛速度方面有明显提高，而且对于部分高维问题（低于1 0维）效果也有一定程度的提升。

四、结论

论文通过对于固定宽度的直方图模型的分布估计算法加入概率阈值的要素，可以防止函数早熟，使用固定区间宽度提高算法的运行速度，在更新种群步骤中加入模式搜索法，可以有效地提高逼近解的精度。

针对更高维的问题如何找到一些好的改进方法以及如何进一步提高最优值的精度，都需要继续深入研究。

[1]周树德,孙增圻.分布估计算法综述[J].自动化学报,2007，（2）:113-121.

[2]陈宝林.最优化理论与算法(第二版)[M].北京：清华大学出版社，2009:332-336.

[3]严宇平.运用改进直方图模型的分布估计算法求解连续空间优化问题[D].中山大学硕士学位论文，2010.

[4]张庆彬，吴惕华，刘波.自适应实值分布估计算法[J].清华大学学报（自然科学版），2008，(S2):1859-1862.

[5]熊盛武，刘麟，汪洋等.基于贝叶斯网络的并行分布估计算法研究[D].武汉理工大学硕士学位论文，2005.

O

A

1 6 7 3-0 0 4 6（2 0 1 2）8-0 1 4 7-0 3