基于FANUC-0i系统下螺旋槽宏程序的研究
张 斌
(江苏省张家港职业教育中心校,江苏 张家港 215600)
在数控编程中,常见的编程方法有手动编程和自动编程。手动编程在院校教学中应用的较多,因为手动编程是编程的基础,需熟练掌握才能为今后的自动编程打下基础,而自动编程则在企业生产中应用较广,主要是为了提高加工精度和生产效率,以便获得更多的经济利润。手动编程不仅可以实现简单的轮廓编程,如直线、圆构成的轮廓,还可以实现二次函数曲线轮廓编程,如:椭圆、抛物线、双曲线构成的轮廓。上述轮廓编程比较常见,那对于螺旋槽这样的宏程序又是怎样编程的呢?现通过实例来介绍FANUC 数控系统螺旋槽宏程序的编制。零件图尺寸及实体模型,如图1 所示,函数方程为R=0.035×a+22。
1 螺旋线槽的宏编程
1.1 分析图形特征
(1)零件分析:毛坯直径为120 mm 的圆柱体,中间是截面沿螺旋线构成的槽。具体尺寸见图1 左所示。
(2)工艺分析:用精密平口钳装夹底部合适位置,先粗、精铣表面外圆轮廓,保证精度,再铣削螺旋槽。
(3)刀具选择:T01,准8 mm 硬质合金铣刀。只进行螺旋线编程,其余程序省略,最后加工形状见图1右所示。
1.2 建立数学模型
螺旋线方程为R = 0.035 × a + 22,a ∈ [0 ~450°],其数学模型参照图2 所示。
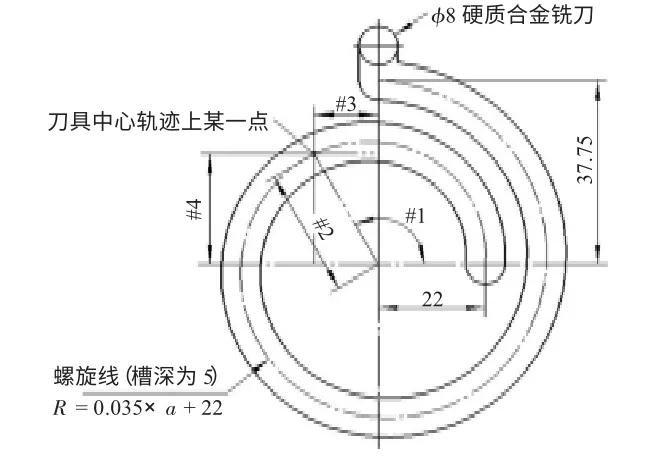
图2 螺旋线槽数学模型
1.3 编程思路
根据螺旋线方程R=0.035×a +22,a ∈[0~450°]可知,该螺旋曲线的半径值R 是随角度a 的改变而变化的,只要把角度a 作为变量,就可以计算出该角度时的半径R 值,并通过圆的参数方程X=R×cos a,Y=R×sin a,就能得出X,Y坐标。采用铣刀中心编程,即铣刀中心沿该螺旋线轨迹走刀。
1.4 变量设定
螺旋线角度初始赋值#1 =450;螺旋线半径值#2=0.035×#1+22;螺旋线半径在X 向的坐标值#3=#2×cos[#1];螺旋线半径在Y向的坐标值#4 =#2×sin[#1]。
2 实例加工
2.1 参考程序
实例参考程序如表1 所示。
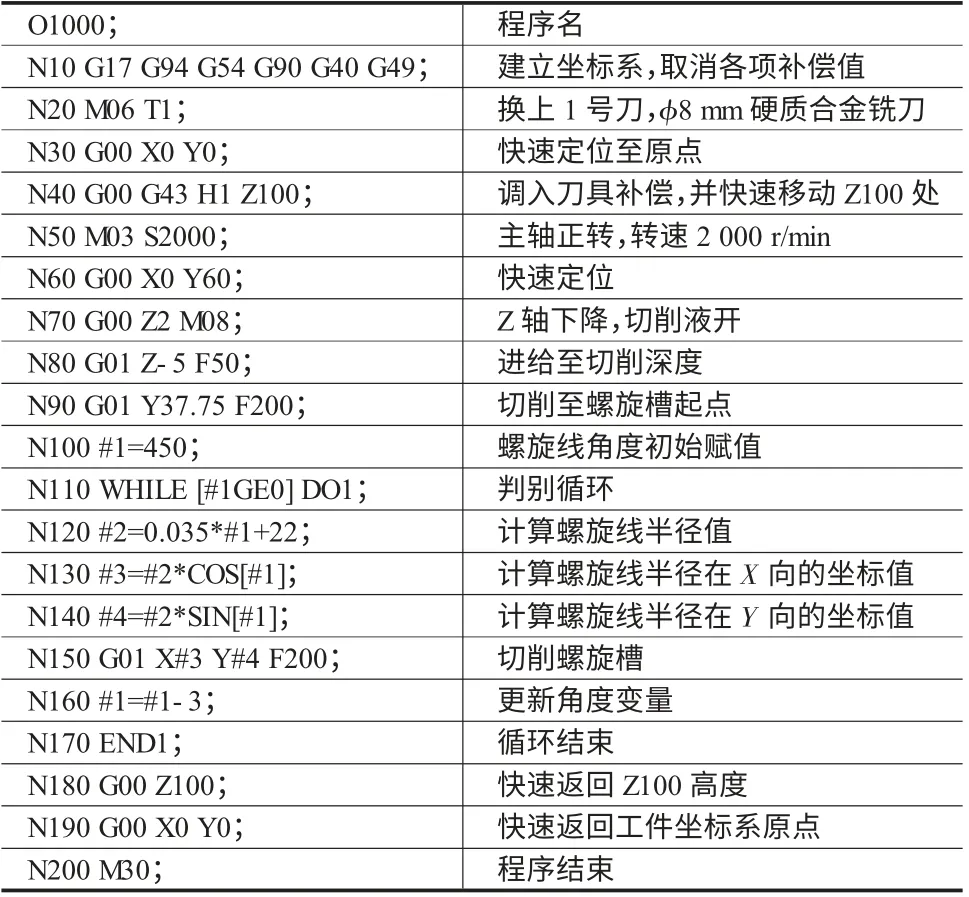
表1 实例参考程序
2.2 实物零件
根据上述分析,输入程序,并进行对刀与加工,其最后加工零件如图3 所示。

图3 螺旋槽零件
3 结束语
在铣削平面的曲线轮廓时,只要给定曲线的函数方程,确定好变量值,通过计算该曲线上的点的坐标值,即可实现正确的宏编程。那么在铣削螺旋线槽时,也是采用同样的方法。可见,在进行平面曲线编程时,只要掌握宏程序编程方法,不管遇到什么样的曲线轮廓,都能轻松解决。
[1]陈海舟.数控铣削加工宏程序及应用实例[M].北京:机械工业出版社,2007.

