基本过程能力指数的分析与应用问题研究
韩亚利
(长沙航空职业技术学院,湖南 长沙 410124)
在生产过程的质量分析与控制中,计算与评价过程能力指数是一项非常重要的工作。特别是近年来,随着计算机技术的迅速发展,开发了很多质量管理和质量控制软件,使得在计算过程能力指数值时,所需要的大量数据的实时收集、计算和分析,可以借助于计算机软件来轻松地实现,极大地促进了过程能力指数的理论研究和在生产实际中的应用。
过程能力(Process Capability,PC)以往称工序能力,现已根据ISO 标准规定,统一称为过程能力,是指在生产过程处于稳定状态时,该过程所生产的产品能满足质量要求的能力。而过程能力指数(Process Capability Index,PCI)则是将过程能力量化后的评价标准,表示过程能力满足质量技术标准(产品规格、公差)的程度。
经过长期的理论研究和实践,从事数理统计质量控制的研究人员提出了许多种过程能力指数。根据文献的不完全统计,目前已在实践中应用和正在进行研究的单变量过程能力指数多达20 多种,多变量过程能力指数也有7 种。但从研究的原理和过程来看,这些过程能力指数都是从Cp、Cpk、Cpm和Cpmk等4个基本指数的基础上发展、变化而来的[1]。它们之所以被称为基本指数,首先,是因为它们是最早提出来的(1986年,美国质量专家V.E.Kane 在公开发表的文献中就系统地介绍了这4个指数)、也是最简单的指数(单变量指数);其次,还因为这4个指数都是建立在过程特性值服从最常见的正态分布假设之上的,是当生产过程处于稳定状态时进行过程能力分析与评价的、最常用的几个指数。因此,正确理解、把握、解释这几个基本过程能力指数的定义、概念和应用特点就显得尤为重要。
1 过程能力指数
对于稳定受控的生产过程,由于不可避免地存在各种随机因素的作用,其过程特性值总呈现一定的分散性。在一般情况下,过程特性值服从正态分布N(μ,σ2),其中μ 为过程特性值的总体均值,σ 为过程特性值的总体标准差。在正态分布曲线图上,T=Tu- Tl为技术规格的公差幅度,Tu、Tl分别表示上、下规格界限,技术规格的公差中心
1.1 第一代过程能力指数Cp、Cpk
(1)过程能力指数Cp。美国著名质量专家朱兰(J.M Juran) 在1974年首先提出了用统计控制状态下的6σ 表示的过程能力指数Cp,其定义式为:

在Cp定义式中,T = TU- TL反映产品质量的设计要求,总体标准差σ 反映了过程特性值的分散程度,可通过计算样本标准差S 来估计。所以Cp定义式将6σ 与T 比较,就反映了过程质量满足产品质量设计要求的能力,定量的表征了该工艺过程满足技术规范要求的能力。Cp值越大,表明该工艺过程满足技术规范要求的能力越高,但对设备和操作人员的要求也越高,相应的经济成本也越大。
Cp就是通常所说的过程能力指数,该指数讨论的是过程特性值均值μ(分布中心)和技术规格的公差中心M 重合一致的情况,即μ=M,但这只是一种理想的状态。因此,Cp值仅表示工序过程能力的潜力,又称为潜力过程指数。
(2)实际过程能力指数Cpk。在实际生产过程中,经常有分布中心与公差中心不重合的情况,即μ≠M有偏移量ε,如图1 所示。
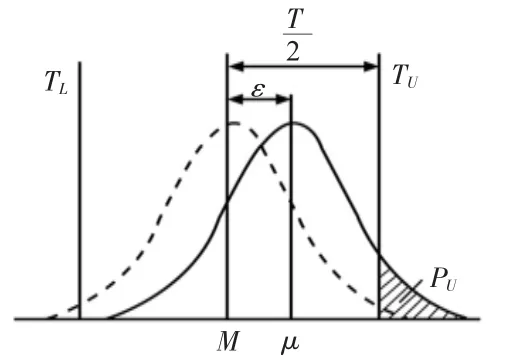
图1 μ≠M 有偏移量ε 时的情形
从图1 可得知,当μ≠M 有偏移量ε 时,不合格品率PU明显增大,过程能力减小。此时,Cp已不足以反映有偏移的实际情况,需要加以修正。
美国质量专家V.E.Kane 在1986 提年出了需要定义一个校正因子来表征偏移量的大小,并将修正后的指数Cpk定义为:
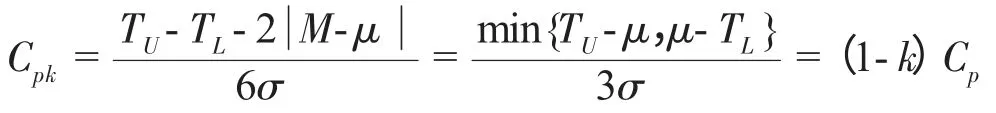
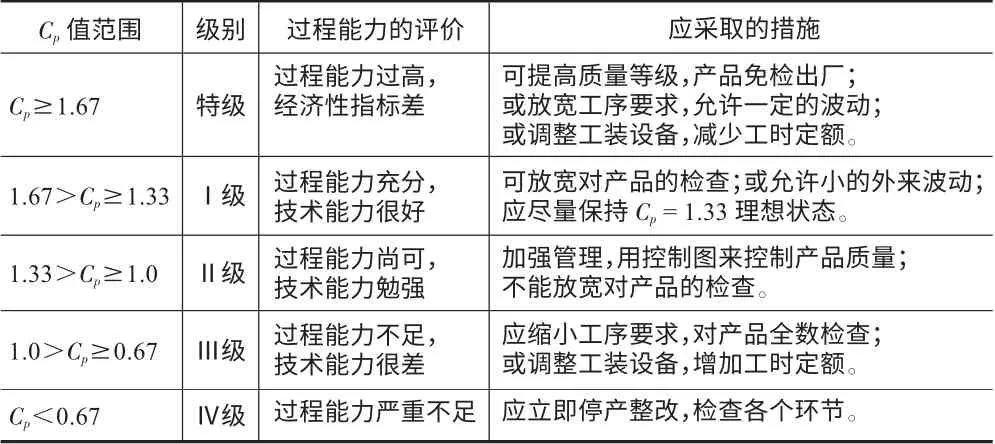
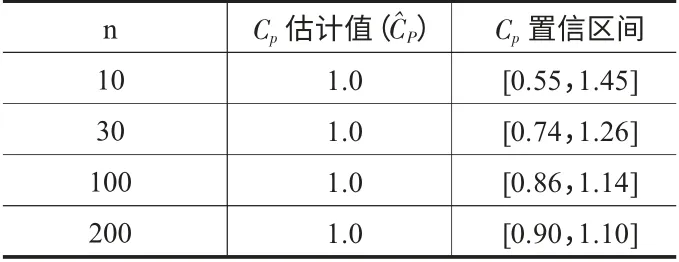
显然,偏移系数0≤k≤1。即:当μ≠M 时,Cpk CPk的定义式充分考虑了分布中心μ 与公差中心M 之间的位置关系,克服了Cp指数的缺陷。因此,Cpk在实际生产过程中比Cp应用更多,很多质量研究学者又称其为实际过程能力指数[2]。 虽然Cpk考虑了μ 偏移M 的程度,但对于μ 偏离目标值T 的情况仍无法反映。无论Cp还是Cpk的定义式,对于给定区间(TL,TU)内的μ 值,当σ →0 时,Cp和Cpk都会发散至无穷大,因此Cp和Cpk不能很好的用于过程集中程度的度量。针对指数Cp和Cpk的缺点,一些质量研究学者又在此基础上进行了修正,并引入田口损失函数期望值的概念,将其定义为“田口指数”CPm: 其中:σ'2= E[(Y-T)2],表示Y 偏离目标值T 的方差的期望。 由于田口指数CPm的设计考虑到μ 与T 之间的关系,故无论使过程方差变大,还是过程偏离目标变大,都会引起CPm的减小,因此,CPm能综合反映过程偏离目标的离散程度。 该指数把顾客期望的理想值(也即目标值)引入进来,体现了Taguchi 质量管理思想——产品偏离目标值就会有质量损失。所以CPm在反映过程期望损失的能力上要明显优于CP和CPk,通过计算CPm可以对过程的经济性进行客观的估计。这就是CPm与Cp、Cpk的本质区别。 Pearn Kotz 和Johnson 将CPk和CPm的 优 点 相 结合,于1992年提出了过程能力指数CPmk的定义: 由定义可知,CPmk同时考虑了μ 与M 及T 之间的关系。Peam Kotz 同时还证明,当T=M 且μ=T 时,CPmk指数比CPk和CPm都灵敏,即CPmk的下降速度最快。因此,CPmk指数能同时反映过程的不合格品率和期望损失[2]。 CPmk又称为混合指数,由CPk的分子与CPm的分母混合而成,其对过程能力的综合评价效果要好于CPk和CPm。但是,研究表明在很多情况下该指数与实际生产过程也还是有一些差距[3]。 对过程能力评价的基本原则是:既要考虑生产过程有充足的过程能力,又要考虑生产过程有合理的经济性指标。在一般情况下,由抽样采集的样本数据计算出过程能力指数后,即可根据Cp、Cpk值对过程能力进行评价,如表1 所列;如果存在偏移系数k,则需要根据Cp、Cpk值的大小对某些参数进行处理,如表2 所列。 表1 过程能力指数Cp 值评价标准 表2 存在偏移系数k 时的处理 上述Cp值评价标准只是传统的一般要求,只能作为实际工作的参考,其它几个过程能力指数的评价标准可参考有关文献资料。 需要说明的是,所谓过程能力不足或过高,都是针对特定生产制造过程以及特定产品的特定工序过程而言,不应理解为统一的模式。例如,当Cp叟1.33时,过程能力充分满足质量要求,故在ISO9000 标准中要求Cp叟1.33;而在一些企业推行的六西格玛管理模式中,则要求Cp值达到2,这是现代企业的高标准、严要求,也是高新技术发展的必然。 由已知条件计算可得,公差中心M=20.007 5;又已知分布中心向右偏移,偏移量ε=偏移系数k=0.2,过程能力指数Cp=0.933。 由表1 所知,Cpk=0.933,在1.0>Cpk叟0.67 范围内,属于Ⅲ级过程能力,表现为该工序的过程能力不足,质量保证能力较差;应分析原因,采取工艺措施,提高过程能力以保证产品质量。具体有以下几种途径: (1)针对零件设计功能,适当加大内孔公差范围,减少工序加工难度; (2)选用高精度机床设备,减少偏移量ε,提高工序加工精度; (3)查找原因,确定质量改进方向,减少过程特性值的分散程度σ。 随着计算机技术的发展,过程能力指数的计算和分析已非常简便、快捷,但在实际工作中,质量管理人员还是会出现一些技术问题,使得他们不能很好地利用这一质量工具来分析、评价过程能力。本文主要涉及与过程能力指数的定义、特征有关的两个技术问题的处理。 在实际生产现场的质量控制中,有些质量管理人员为了节省抽样时间,只抽取少量的样本数据就计算过程能力指数,这样往往会导致其分析结论和生产过程的实际情况产生很大差异。 根据数理统计学原理,这种基于样本得到的过程能力指数估计值本身就会产生估计偏差。特别是,当抽取的样本容量n 太小、且样本中还存在某一个或几个异常值时,就将很难保证抽样结果反映出随机性变量的主要特征。即这些异常值的存在会影响到数据分布的正态性,对样本均值和标准差的计算带来很大误差,从而使过程能力指数严重失真。 当样本容量n 很小时,过程能力指数的置信区间也会很大。我们可以根据抽取的样本数据,计算当过程能力指数的估计值=1 时,不同的样本容量n所对应的CP置信区间,如表3 所列。 表3 与样本容量n 对应的Cp 置信区间 事实上,在小样本条件下(n 小于20 ~ 30)难以判定过程特性值数据分布的正态性,也很难说明在抽样时,过程是否处于稳定或受控状态,计算出的过程能力指数值可能和实际值有很大的偏差。因此,有些统计质量学专家质疑、反对在小样本条件下计算过程能力指数[4]。 在抽样的过程中,难免会发现有些抽样数据明显与其它数据不同(异常值)。因此,在计算和分析过程能力指数时,应结合使用控制图等质量工具,通过数据分布检查有无异常波动或异常值存在。异常波动对质量的影响大,但采取措施不难消除,故在过程中一旦发现异常值,就应该尽快追踪其原因,采取措施加以消除,并纳入标准,保证它不再出现。若找不到导致异常值的原因,则不能随便剔除抽样数据。 基本过程能力指数的定义都设定过程特性值服从正态分布,当数据分布为非正态分布时,基本过程能力指数定义的理论基础就不成立,此时计算过程能力指数是毫无意义的。因此,在得到样本数据后,首先就要检查数据分布是否为正态分布。有些现场质量管理人员在计算过程能力指数时,往往会忽视对数据分布的正态性检验,直接就根据抽取的样本数据计算均值和标准差,这样往往会造成误判。 当过程特性值不服从正态分布时,对基本过程能力指数进行修正的理论研究成果很多,但这些非正态分布总体下的指数设计方法,均具有一定的主观性,大多比较抽象,不便于实际使用者掌握。但是,对于某些由于特殊的工艺原因导致数据分布非正态的情况,为了仍然能够应用过程能力指数表征工艺过程的质量保证能力水平,可通过一些简单的转换方法,尽量把非正态数据转换成正态,然后根据转换后的数据计算过程能力指数[5]。 等效指数转换是一种能应用于生产实际的、较为简便的方法。等效指数转换的主要思路是通过计算过程特性值的不合格品率,以在同样不合格品率的情况下,当质量特征值的均值和目标期望值重合时的过程能力指数作为等效过程能力指数。这样,过程能力指数就和过程特性值分布类型无关,且只与工艺成品率对应。对于总体均值与公差中心不重合时存在的偏离,也可以计算得到存在偏离时的等效过程能力指数。用这种方法处理非正态数据比较直观,容易理解,具体的转换方法可参考有关文献资料。 科学地计算和分析过程能力,可以清楚地了解和评价过程质量水平,对于产品设计、工艺制定、计划安排、生产调度和技术改造等方面都具有重要意义,同时也是一项非常复杂的、技术难度很高的专业性工作。本文通过对上述几个基本过程能力指数的定义、特点的研究,给出了各种指数的应用特征和范围,能够为生产现场的质量管理人员进行过程能力分析、评价提供指导,也为建立计算机系统模块提供了清晰的数学模型和相应的数据支持。 [1]刘光第.质量管理学(第二版)[M].北京:清华大学出版社,2003. [2]龚益鸣.质量管理学[M].上海:复旦大学出版社,2000. [3]钱中侯,张公绪.质量专业理论与实务[M]. 北京:中国人事出版社,2001. [4]张公绪.质量专业工程师手册[M].北京:企业管理出版社,1994. [5]张公绪,孙 静.新编质量管理学(第二版)[M].北京:高等教育出版社,2003.1.2 第二代过程能力指数CPm
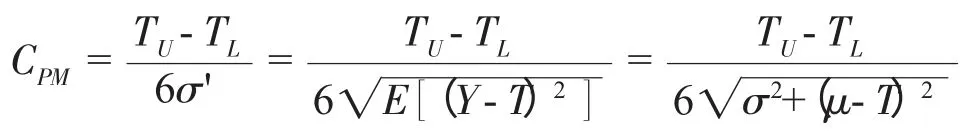
1.3 第三代过程能力指数CPmk

2 过程能力的分析和评价

3 几个技术问题的处理
3.1 样本容量和异常值的处理
3.2 非正态分布的等效指数转换
4 结束语

