小型蛇形机器人的蠕动运动分析与仿真

陈 涛，李连波

（南京理工大学泰州科技学院，江苏 泰州 225300）

蛇形机器人，又称机器蛇，其是一种能模仿生物蛇运动的新型机器人。由于其能像蛇一样进行“无肢运动”，因而被国际公认为“最富于现实感的机器人”。

随着机器人研究领域的迅速发展，航空航天、军事侦察攻击、水下地下管道勘测、疾病检查治疗、救灾抢险、星际探索等非结构环境下的自主作业已成为了重要的热门研究发展方向。针对未来的机器人未知的工作环境，蛇形机器人的研究开创了一个新的仿生机器人的研究领域，其多关节、多自由度，多冗余结构可实现多种运动模式，颠覆了靠轮子或者履带通过连续转动的方式实现地面运动的传统方案，具有极强的灵活性、稳定性和环境适应能力，在完成非结构环境下的自主作业方面具有极强的研究价值。蛇形机器人研究的广阔前景和潜力，使得近年来国内外很多研究者都在致力于推动蛇形机器人的研究和发展，并取得了许多成绩。

1 蠕动运动的运动分析与仿真

蛇形机器人的蠕动过程可以近似看作是运动连杆依次传动的过程[1]。将蛇形机器人简化为八段固定长度的连杆系统，蛇形机器人的蠕动过程需要多关节的协调运动[2]。本文以4 连杆组成的蠕动运动分析为重点，对如何使得波形过渡得较平滑，不会出现大的角速度变化，且尽量避免静止端出现滑动等问题进行分析讨论。

依据蜿蜒曲线的定义，可得蛇形机器人在进行近似于蜿蜒曲线半波形状态的向前伸缩运动时，相邻的连杆间的角度变化函数，即关节角度函数

设定T 为半波形传播周期。其中，

i 的取值为[1，n-1](n 取4)；

A 表示关节角度函数的幅值；

B 表示相邻关节间的相位角；

R 为关节角度的相位偏差，由于蠕动运动中总保持直线向前，故R 取0；

w 为波形推进的速度[3]。

令t =0 时，可以得到各个连杆在初始位置的关节角

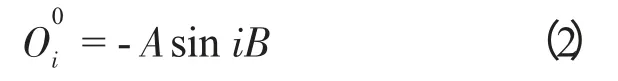
由于在初始位置时刻的波形是关于Y 轴对称的，因此，可以求出运动波形在第1 和第n 杆件的初始角度[4](n 取4)

当相邻两波形推进时，理想情况下，运动波形的第1，2…，6 的关节角，同Oi一样，也是发生正弦变化，因而可得出各个关节的相对角速度为：

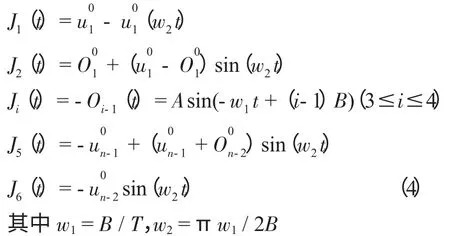
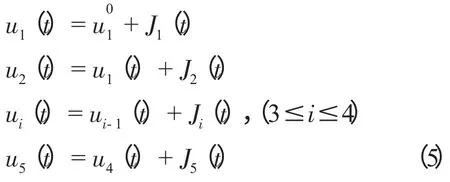
根据上面所推导的公式，可以对蛇形机器人的蠕动运动过程进行仿真，取n=4，因此相位差B=180/n=45°，杆长l 为0.075 m,w1=B/T=π/4T，w2=πw1/2B =π /2T，(T 取2) 仿真结果如图1 所示，横纵坐标分别为关节运动时在水平面和垂直面的位置。通过仿真实验，可以得到各个时刻动杆的位置，同时可以得出幅值A 对蠕动轨迹的影响规律，A越大，产生的波峰越陡。取A =45°时，波形曲线最佳，另外半波形传播周期T 的取值对其运动轨迹没有影响。

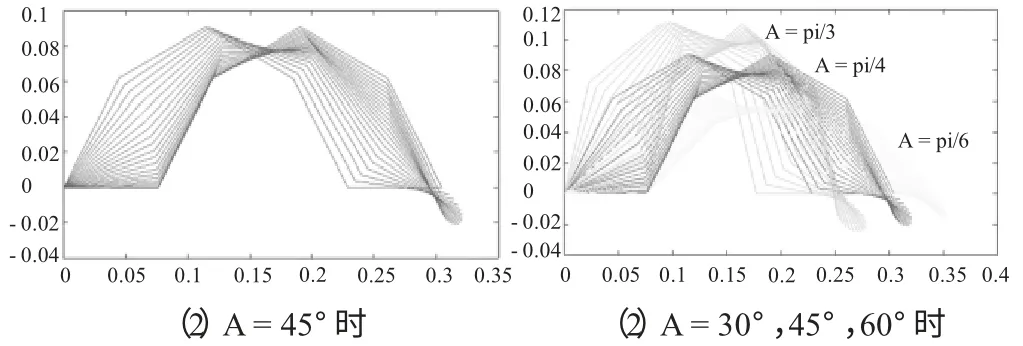
图1 蠕动运动半波形传递过程仿真

2 蠕动运动的动力分析与仿真

在对蛇形机器人蠕动运动过程的运动学进行了分析的基础上对其动力学方面进行分析，为蛇形机器人的运动控制提供理论依据。对蛇形机器人的蠕动过程动力分析，其中一个重点是对马达进行驱动校核。本文以校核运动中，对舵机的驱动力矩是否满足这部分的要求为重点，对蛇形蠕动运动过程展开研究。

运动中舵机的驱动功率，取决于其施加给关节的力矩和转速。力矩大、转速高的电机，其输出功率就大，当然电流也会相应增大。如图2 所示，由受力分析可看出，关节所受的压力由波形的顶端向两端逐渐增大。故相应电机所受力矩也逐渐加大。所以波形两端所受的力矩是最大的。

对蛇形机器人的四连杆机构的蠕动运动过程中所需的最大的驱动力矩进行校核，通过仿真实验可得：最大驱动力矩(单位N·m)与时间t 的关系如图3所示(取n=4，B=180/n=45°，w1=B/T=π/4T，w2=πw1/2B =π / 2T，l =0.075 m，m =0.12 kg)，由图3 可以看出对于蛇形机器人的蠕动运动过程中的所需的最大驱动力矩不随运动周期T 的变化而变化，但随A 的增大而减小。结合之前的运动仿真分析，取A =45°较合适。从图中可读出最大驱动力矩为0.252 N·m，又由于舵机的效率η =80 %，可得出以下结论：当n=4，B=45°(相位差)，A=45°(幅值)，l =0.075 m(杆长)，w1=π / 4T，w2=π / 2T 时，完成蛇形机器人的蠕动运动，其舵机的驱动力矩至少为0.315 N·m。

图2 蛇形机器人蠕动运动过程中的动力学模型

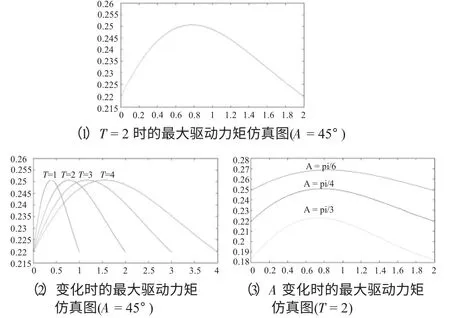
图3 四连杆组成的蠕动运动中最大驱动力矩仿真图

3 结束语

本文建立了蛇形机器人的关节轴平行于的面的蛇形机器人的蠕动运动的动力学和运动学模型，进行蠕动运动轨迹的设计，根据蜿蜒曲线方程推算出了一种近似于蜿蜒曲线的半波形传动的蠕动运动轨迹公式，通过仿真验证了四连杆组成的蠕动运动规划是合理的，校核最大驱动力矩。

[1]赵铁石，林永光，缪 磊，王春雨.一种基于空间连杆机构的蛇形机器人[J].机器人，2006，28（11）：629-636.

[2]胡友耀，丁建宁，杨继昌，范 真，张占立，等.蛇类表皮的生物摩擦学性能研究.润滑与密封，2006，(11):56-59.

[3]孙 洪，马培荪，王光荣. 蛇形机器人一种基于serpenoid 曲线的蠕动步态[J]. 机械设计与研究，2008，24（1）：39-41．

[4]薛瑞彬，苏 中，张夏丽，万承军.蛇形机器人直线运动的研究[J].北京信息科技大学学报，2011，（5）：65-69.