立体几何解答题处理策略

☉浙江省温州市啸秋中学 郑上典

立体几何解答题处理策略

☉浙江省温州市啸秋中学 郑上典

本文下面介绍解答立体几何问题的几个切入点，虽然这些方法对于老师并不陌生，但对学生而言，能够较快地找到解题的入口，则对教学有借鉴.

立体几何的解答题是高考的必考题型，这类问题以空间的线、面关系为载体，主要考查学生的空间想象能力、推理论证能力等.但学生在解答这类题时，往往有畏惧感，盲目探索，浅尝辄止，甚至感到无从下笔.因此有必要对这类问题的解题策略作一些探讨.

一、作好辅助线

证明线线平行、线面平行时，若有三角形、梯形一边的中点，常取另一边的中点作出中位线，利用三角形、梯形中位线的性质证题.

当有等腰、等边三角形时，常找底边的中点连成中线，利用等腰、等边三角形的底边的中线即为高线，从而作出垂直关系.

有正方形这个条件时，常连接对角线，利用正方形的对角线互相垂直平分来得到垂直关系.

例1 图1是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC.已知A1B1=B1C1=1，∠A1B1C1=90°，AA1=4，BB1=2，CC1=3.

（1）设点O是AB的中点，证明：OC∥平面A1B1C1；

（2）求二面角B—AC—A1的大小；

（3）求此几何体的体积.

证明：（1）由题意四边形AA1B1B是直角梯形，且点O是AB的中点，所以想到取A1B1的中点O1，连接OO1，则OO1是梯形AA1B1B的中位线.

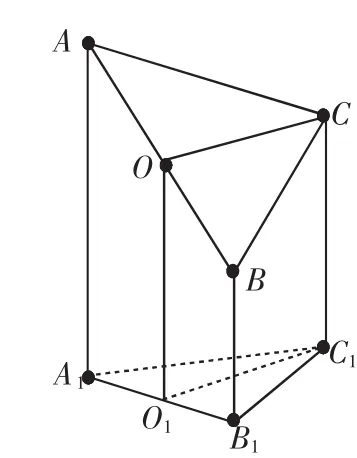
图1

点评：此例就是利用三角形、梯形的中位线的性质证题，过程自然、合理.

二、合理猜想

例2 如图2，在直四棱柱ABCD－A1B1C1D1中，已知DC=DD1=2AD=2AB，AD⊥DC，AB∥DC.

（1）求证：D1C⊥AC1；

（2）设E是DC上一点，试确定E的位置，使D1E∥平面A1BD，并说明理由.

证明：（1）在直四棱柱ABCDA1B1C1D1中，连接C1D.

由DC=DD1，得四边形DCC1D1是正方形，则DC1⊥D1C.

点评：DC1⊥D1C就是利用正方形的对角线互相垂直证得.

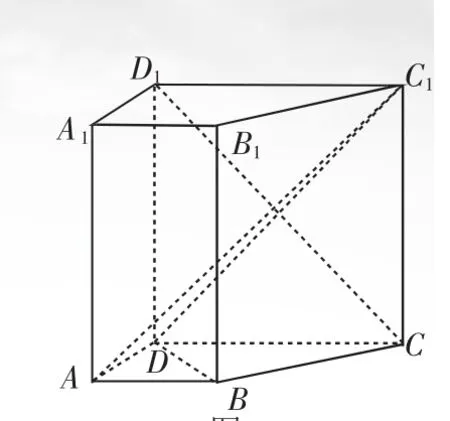
图2

（2）由于本题证明的是线面平行，平行的问题多和中点有关，所以先猜想使E成为DC的中点时的情况再论证，理由如下：当E是DC的中点时，连接BE，则有BE∥ADA1D1，则四边形A1D1EB是平行四边形，D1E∥A1B.

点评：利用平时积累的经验“猜想”也是数学发现的重要手段，在日常教学中要注重培养学生“先猜想后证明”的数学意识.

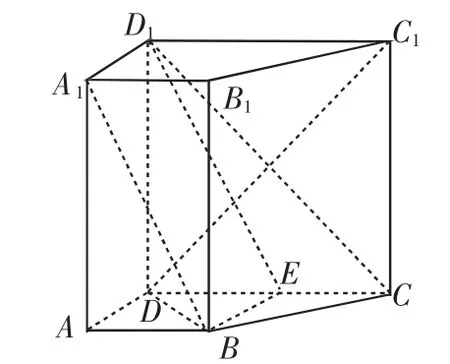
图3

三、挖掘隐含

当题目中告诉一些边长或角的值时，一定要记得通过计算或论证发现有等腰、等边三角形或通过a2+b2=c2或者计算角的度数发现有直角三角形.

例3 如图4，在三棱锥S－ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC=90°，O为BC的中点.

（1）证明：SO⊥平面ABC；

（2）求二面角A－SC－B的余弦值.

证明：（1）连接OA，由题设SB=AB=SC=AC，BC是公共边.

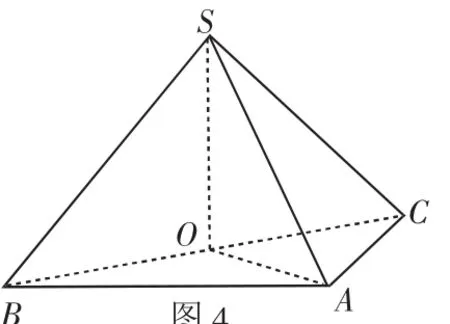
图4

（2）略.

点评：本题容易发现SO⊥BC，但若不利用边长间的关系SO2+AO2=SA2，不易发现SO⊥AO.

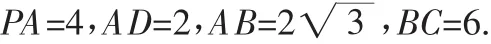
图5

（1）求证：BD⊥平面PAC；

（2）求二面角A－PC－D的大小.

证明：（1）由PA⊥平面ABCD，BD⊂平面ABCD，得BD⊥PA.

（2）略.

点评：本题易得BD⊥PA，只要有“利用好边长计算的意识”，计算出∠ABD=30°，∠BAC=60°，就能证得BD⊥AC.

高考解答题是能力与时间的角逐，赢得考试时间对考生来说至关重要，这就要积累平时的解题经验与捕捉他人之“玉”，要善于总结和比较，总结出题目类型，比较出最优方法，考场上就会胸有成竹，就会在竞争中占得先机.