应用数形结合理解三角形四心的向量形式
2012-08-28 01:42:02江西省赣县中学北校区李春满
中学数学杂志 2012年19期
☉江西省赣县中学北校区 李春满
应用数形结合理解三角形四心的向量形式
☉江西省赣县中学北校区 李春满
数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以相互转化.中学数学研究的对象可分为数和形两大部分,数与形是有联系的,这个联系称之为数形结合,或形数结合.作为一种数学思想方法,数形结合包括两个方面:第一种情形是“以数解形”,而第二种情形是“以形助数”.
下面以三角形的四心为出发点,结合向量相关知识,应用数形结合的思想,解决三角形四心所具备的一些特定的性质.既学习了三角形四心的一些特定性质,又体会了向量带来的巧妙独特的数学美感.
一、重心的向量形式应用

A.外心 B.内心 C.重心 D.垂心
解析:如图1所示,△ABC中,D为边BC的中点.


图1
所以点P的轨迹一定通过△ABC的重心,即选C.
二、垂心的向量形式应用

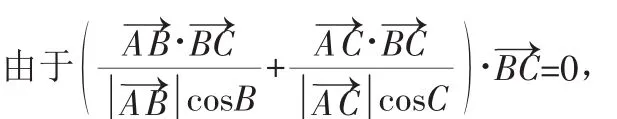
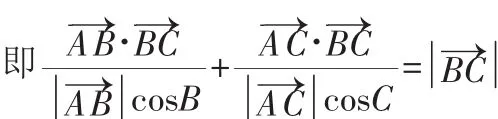

图2

直于BC的直线上,所以动点P的轨迹一定通过△ABC的垂心,如图2,即选D.
三、内心的向量形式应用


图3
四、外心的向量形式应用

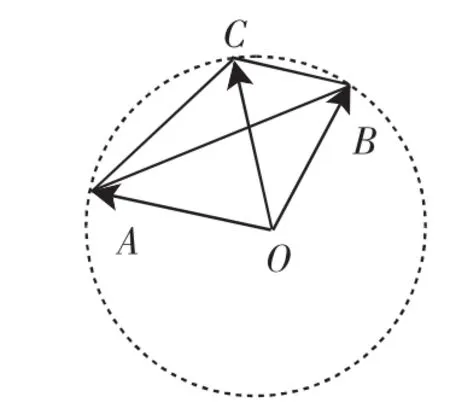
图4
编者注:在平面向量的应用中,用平面向量解决平面几何问题时,首先将几何问题中的几何元素和几何关系用向量表示,然后选择适当的基底向量,将相关向量表示为基向量的线性组合,把问题转化为基向量的运算问题,最后将运算的结果再还原为几何关系.向量不仅是平面解析几何入门内容,而且是解有关数形结合问题的重要工具.它一般通过概念的移植、转化,将坐标与向量结合起来,从而使一些难题在思路上获得新的突破.
猜你喜欢
中学生数理化·高一版(2023年2期)2023-03-23 02:17:02
江苏科技报·E教中国(2021年9期)2021-07-23 16:28:20
少先队活动(2020年8期)2020-09-11 06:43:12
少先队活动(2020年7期)2020-08-14 01:18:12
广州文博(2020年0期)2020-06-09 05:13:44
蜜蜂杂志(2020年8期)2020-03-05 11:44:26
教师博览(2019年5期)2019-05-21 05:56:12
老年教育(老年大学)(2017年5期)2017-07-03 14:48:49
新闻前哨(2016年11期)2016-12-07 11:41:34
新教育时代·教师版(2016年27期)2016-12-06 18:19:56

