从消参的角度探析一道解析几何题的简解

☉河南省登封市实验高级中学 杨建筑

从消参的角度探析一道解析几何题的简解

☉河南省登封市实验高级中学 杨建筑

2011年郑州市高中毕业年级第三次质量预测理科第20题（文科压轴题）是一道较难的解析几何题.该题主要考查直线与椭圆的位置关系，其解答的核心思想是消去“非对称目标函数”中的参数.试题和标准答案如下：

（1）当D点到两焦点的距离之和为4，直线l⊥x轴时，求k1∶k2的值；

（2）求k1∶k2的值.

解：（1）本小题的结果为k1∶k2=3.解答过程略.

所以k1∶k2=3为所求.

12直接消去参数.

点评：本解法的消参方法，思路简捷，操作简便，运算简单，既没有原答案中的两个“转化”和一个“判断”（即将关于y1、y2的对称式转化为关于x、x的对称式，将非对称代数式升幂转化

12为对称代数式③，判断的符号），又没有应用韦达定理（这与新课标初、高中都没有涉及韦达定理相一致）.其最大优点是：无论“目标函数”是否对称，运用此方法消去参数都适合，也是处理此类问题的通性通法.

分析2：利用式①整体消去y1·y2，代入消去y1或y2.

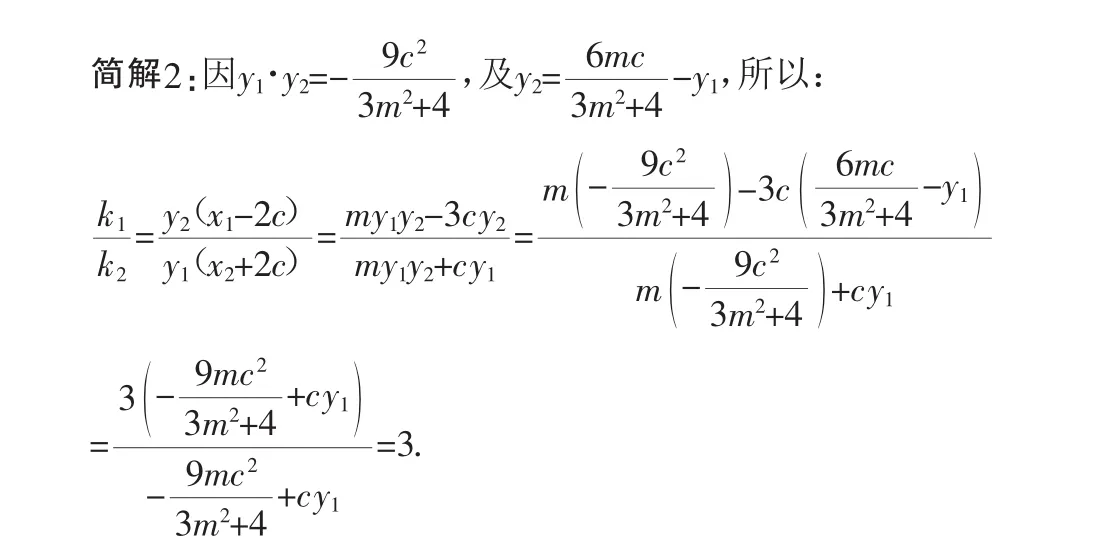
点评：本解法的特点是整体消参和代入消参联合运用.

点评：此解法的特点是代入消参和逆消参综合使用.

分析4：显然，第一小题是第二问的极特殊情况，由此可大胆猜想结论为k1∶k2=3，然后证明之.

点评：此解法的特色是将非对称的消参求值题转化成对称的消参证明题.