直线和圆锥曲线综合题的四个突破口
☉江苏省宝应县安宜高级中学 程守权
直线和圆锥曲线综合题的四个突破口
☉江苏省宝应县安宜高级中学 程守权
直线和圆锥曲线的综合问题是以直线与圆锥曲线为载体,以函数、不等式知识为工具,融几何、代数、三角于一体,具有较强综合性的一类题目,多年来一直是高考命题的热点.然而笔者在教学中发现,许多同学做这类题时,常因找不到问题的突破口而苦恼不已.下面给出解决这类问题的四个突破口,供参考.
一、找定点、定值为突破口


评注:求解直线和圆锥曲线的最值问题时,首先要弄清题意,理顺各变量之间的关系,分清“变”中的“不变”.当问题中有定点、定值时,应尽量先求出来,然后充分利用定点、定值的性质解题.
二、构造目标函数为突破口

图1

(1)求椭圆C的方程.


评注:解决此类问题的方法是根据已知条件和信息,结合相关知识,建立目标函数或不等式,然后求出所求范围.
三、巧选变量为突破口
例3 设以原点为圆心,r为半径的圆与抛物线y2=x-1相交于P、Q两点,设θ=∠POQ(0<θ<π),当r为何值时,θ最大?

解:设抛物线y2=x-1与圆在第一象限的交点为P(x0,y0).
因P在抛物线y2=x-1上,则点P的坐标为(y20+1,y0)(y0>0).


图2

评注:本题求解的关键是选定变量,搞清“动”与“静”的关系,在“变化”中求“不变”(最值).
四、利用几何性质为突破口
例4 设P是直线l:x-y+9=0上的一点,过点P的椭圆以双曲线4x2-5y2=20的焦点为焦点,试求P点在什么位置时,所求椭圆的长轴长最短,并写出这个具有最短长轴的椭圆方程.
分析:题中要求的是长轴长最短的椭圆,且椭圆必须过直线x-y+9=0上的一点P,联想到椭圆定义,椭圆上任意一点到两焦点的距离和为定长2a,问题转化为在直线l上求一点P,使它到l外两定点F1、F2的距离和最短.这个问题在平面几何中用对称的办法就可解决.
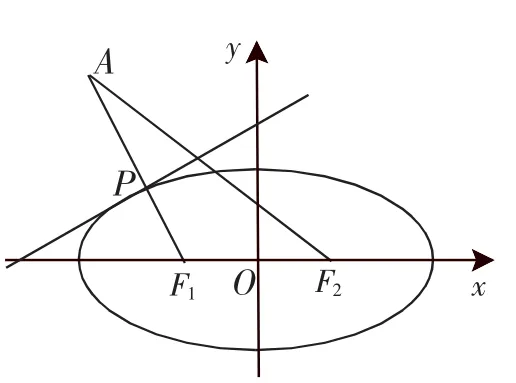
图3

评注:充分利用圆锥曲线的定义和平面几何性质,使最值问题的求解简捷明快.一般来说,可借助平面几何中的对称关系、三角形三边关系、两点之间线段最短等来处理.
总之,求解直线和圆锥曲线的最值问题的方法虽很多,但不管使用哪种方法,其前提都是首先要弄清题意,通过数形结合,找到题目的突破口.

