让数学课堂教学行走在生活的道路上——《向量加法》教学案的设计示例

☉山东省枣庄市第三中学 杨华文（特级教师）

让数学课堂教学行走在生活的道路上
——《向量加法》教学案的设计示例

☉山东省枣庄市第三中学 杨华文（特级教师）

新课程改革的背景下，学生想要的是：自由遨游在数学的天空中，自由呼吸在数学的花园里，自由徜徉在数学的长廊里．在数学的天空里，飞翔着生动，闪烁着鲜活，蕴育着智慧，然而，数学的抽象与逻辑就像一堵墙，在定格数学的同时，也凝固了人们对数学的兴趣．怎么办？……答案无他：实现数学的生活化，让数学课堂教学行走在生活的道路上．

一、导入新课要实现“生活化”

很多老师在教学过程中对导入新课环节不是很重视，其实中学课堂教学的导入新课环节，是整个课堂教学中不可缺少的有机组成部分，是通往精彩的桥梁，是遥控高潮的序幕，更是指引思维的路标．反之，一堂课如果一开始就波澜不惊，学生对接下来的内容是难以提高兴趣的．

向量的加法新课导入案例：

创设情境 直观感知

图1

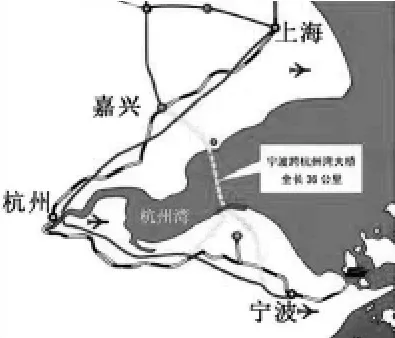
图2

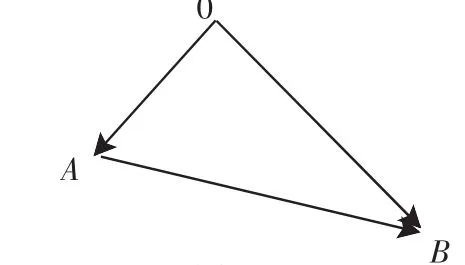
图3

图4

以杭州湾大桥（如图1）为整体背景，设计两个问题情境如下：

问题1：建桥之前如何从嘉兴到达宁波（如图2）？建桥之后可以从嘉兴直达宁波，此时的位移与前面两次位移的结果有何关系（如图3）？两次位移的结果可称为两次位移的和，如何用等式来刻画这三个位移的关系？

问题2：这是大桥南端的A型独塔斜拉桥，其中两根拉索对塔柱的拉力分别为F1、F2（如图4），则它们对塔柱的共同作用效果如何？合力可称为力与的和，如何用等式来刻画这三个力的关系？

力与位移都是物理中的矢量，既有大小又有方向，若去掉它们的物理属性，就是数学中的向量．它们的和也就可以抽象成向量与向量之间的一种运算——向量的加法（引出课题）.

［设计意图］从学生已有的生活经验和物理知识出发，以杭州湾大桥为背景创设问题情境，从而让学生在位移合成、力的合成的基础之上，抽象出向量加法的概念，进而引导学生总结出向量加法的三角形法则和平行四边形法则，以及各自的操作方法与要领，使学生体会到向量加法的实际背景，经历概念形成的过程，领悟到数学概念的本质，体现“数学教学是数学思维活动的过程教学”，容易激发学生的学习兴趣和探究欲望．通过对两个具体问题的分析翻译提炼转化，引出课题．不仅让学生学会对实际问题进行提炼转化的能力.更让学生有耳目一新的感觉，极大地调动了他们探究的欲望和学习的兴趣，并且在向量加法的起始课上，就拉近了生活与数学的距离，实现新课导入的“生活化”．

二、教学手段要接近“生活化”

针对以上两个问题，笔者先是放手让学生小组合作探究，对问题1和问题2有的小组讨论，有的在练习本上边写边画，同学们展开了积极的尝试探究，最后形成全班同学的大合作，使问题得以解决．按照诱思探究教学理念的引领，笔者在大屏幕上投放出了下面的系列问题及解决时间和解决方式．

向量的加法新课探究内容：

1.抽象概括，形成定义

（1）建立数学模型

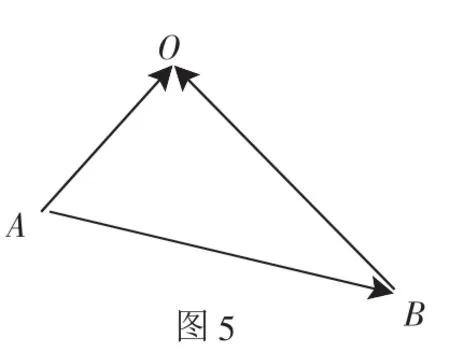
图5

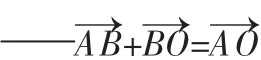
（2）抽象数学概念

问题4：由此，你们能概括出一般的两个向量a与b和的定义吗？

学生活动：在平面内任取一点O，平移a使其起点为点O，平移b使其起点与a向量的终点重合，再连接向量a的起点与向量b的终点．

①平移的目的是什么？——平移后使得两个向量能在同一个三角形中.

②平移后两个向量的终点与起点有何关系？——使得第二个向量的终点与第一个向量的起点重合.

③和向量又是什么？——连接向量a的起点与向量b的终点，并指向b的终点，得到的向量O—→B即为向量a与b的和.

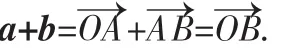
向量的加法的定义：求两个向量和的运算叫做向量的加法．

向量加法的法则：和的定义给出了求向量和的方法，称为向量加法的三角形法则．

问题5：用三角形法则求向量和的过程中要注意什么？——平移两个向量使它们首尾顺次相连．

问题6：还可以用什么方法求两个向量的和呢？——向量加法的平行四边形法则．

问题7：平行四边形法则有何特点？——平移两个向量至同一起点．

两种方法求和的结果是一样的，可见，向量加法的三角形法则与平行四边形法则在本质上是一致的．在具体求和时，应根据情况灵活地选择．

（3）尝试运用法则

试一试：如图6，已知a、b，作出a+b.

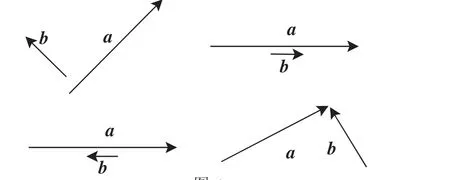
图6

向量加法的三角形法则对共线向量的求和仍然是适用的，反映了三角形法则具有广泛的适用性．

［设计意图］给学生充分的感性材料，在教学中采用了“以问题为中心”的讨论式教学模式．把问题作为教学的出发点，精心设计问题情境，组织相关的数学成分，加强相关内容的联系，使问题处于学生思维的最近发展区，即接近“生活化”，以此激发学生的好奇心与求知欲．并能够较好地培养学生数学地发现问题、提出问题、解决问题的能力．通过学生发现知识从问题中来，培养学生提炼、概括、建立数学模型的能力（一般性探究）．暴露由具体到抽象的思维规律，培养学生的交流合作意识，在探索的过程中获得成就感．避免直接将结论抛给学生，让其从中享受发现的快乐．

2.类比猜想，探究性质

问题8：加法其实我们并不陌生，从小就开始学习数、字母、式的加法，实数的加法有哪些运算性质？向量的加法是否也满足类似的性质？如果满足，具体形式是什么？

实数的加法 向量的加法a+0=a a+（-a）=0 a+b=b+a（a+b）+c=a+（b+c）性质a+0=a a+（-a）=0 a+b=b+a(a+b)+c=a+(b+c)

交换律的验证让学生通过画图自己检验，结合律的验证师生借助于多媒体共同完成.

研究结果表明：向量加法也满足交换律和结合律，这与数的加法是一致的.有了交换律与结合律，向量的加法就可以按任意的组合与任意的次序进行，从而丰富向量加法的内涵.

［设计意图］向量加法运算律的教学，是引导学生通过与数的加法进行类比得到的，并让学生自主探索，构图进行验证．这样不仅体现了学生的主体地位，同时还培养了学生科学的探究能力，归纳推理能力，渗透了数形结合、类比推理等思想．体会数学运算规律的和谐美，和知识来源的“生活化”．

三、教学内容要体现“生活化”

学生在课堂活动中学习的过程就是学生的智慧、情感、体验、思维，生活能力不断生成的过程．所以必须把多种多样的生活化的教学手段引入课堂，让学生真正动起来，活起来，实现师生之间、生生之间的多维互动、思考、交流、讨论，只有这样才能把学生的潜能充分发挥出来．

向量的加法新课探究案例：数学运用深化知识

例1 如图7，O为正六边形A1A2A3A4A5A6的中心，作出下列向量：

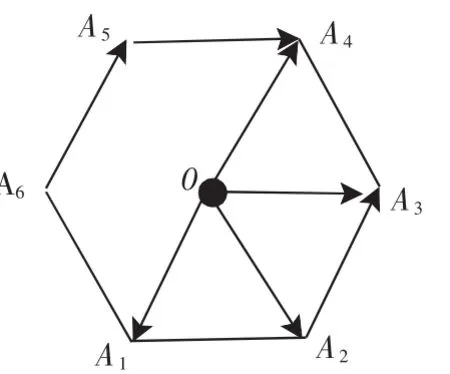
图7

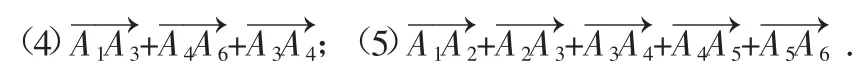
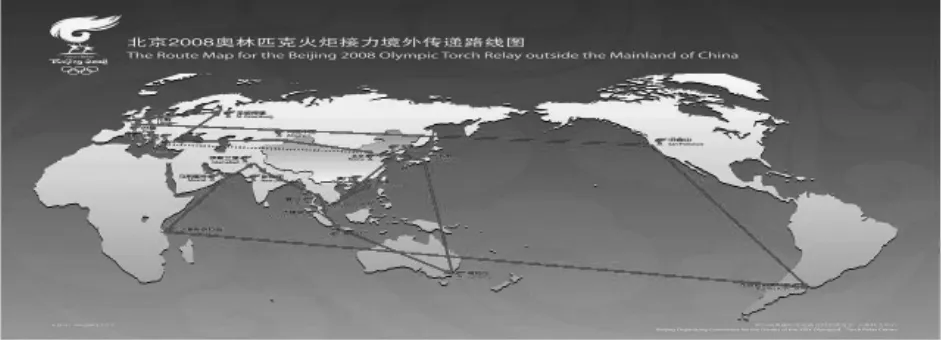
图8

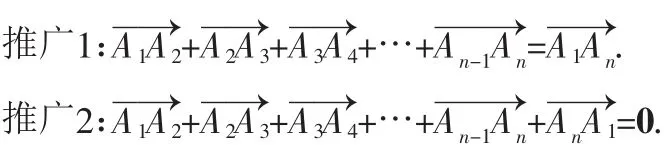
并以2008年北京奥运圣火的传递提供了现实原型（如图8）．

最后我们再回到这座宏伟壮观的大桥来解决这样一个实际问题：

［设计意图］数学课程既要讲逻辑推理，更要讲道理，通过对典型例子的分析和学生自主探索活动，使学生理解数学概念、结论逐步形成的过程，体会蕴涵在其中的思想方法，体现教学内容的“生活化”，追寻数学发展的足迹，把数学的学术形态转化为学生易于接受的教育形态．这是新课程理念中特别强调的，也是笔者备课过程始终如一的追求．

图9

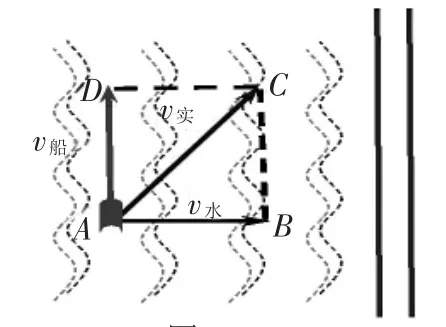
图10

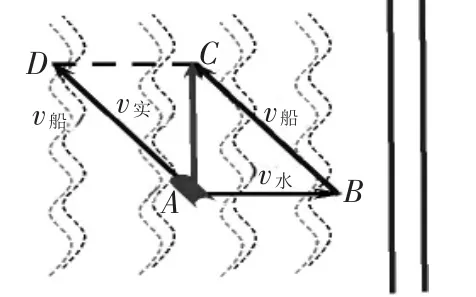
图11

例2 已知桥（如图9）是南北方向，受落潮影响，海水以12.5km/h的速度向东流，现有一艘工作艇，在海面上航行检查桥墩的状况，已知艇的速度是25km/h，若艇要沿着与桥平行的方向由南向北航行，则艇的航向如何确定？

答：若要游艇沿着与桥平行的方向由南向北航行，其航向应为北偏西30°．

［设计意图］以学生比较熟悉的生活问题作为例题，从生活原型中抽象出数学模型，在此基础上去研究数学模型，最后应用到生活实践中去．并再一次告诉我们，数学源于生活，又服务于生活，体现了数学“生活化”平易近人，让学生切身感受生活创造了数学，同时数学美化了生活．

至此学生不仅顺利解决了引例所提出的问题，还自行探究出了向量加法的运算法则，并且还明确了它所满足的运算律，整堂课学生都群情振奋、情绪高昂．因此，实现数学教学生活化、让数学课堂教学行走在生活的路上，是新课程改革的必然趋势，也是我们数学教学的生命之泉．其实，要做到数学教学的生活化，方法远不止这些，“教无定法，贵在得法”，只要我们每一位数学教育工作者抓住新课程改革的重要机遇，切实践行课程改革新理念，做教学的有心人，就一定能给学生营造出一个又一个生活化的数学课堂，奉献出一堂又一堂数学教学的精品.

四、教学感悟

1.精心设计问题，促进深度学习

美国心理学家布鲁纳指出：“教学过程是一种提出问题和解决问题的持续不断的活动，思维永远是从问题开始．”因此，怎样精心设置问题系列，为学生的学习活动搭建恰当的平台，对于一节课的教学走向，促进学生的自主学习和深度学习是非常关键的．本节课，笔者在深入研读教材的基础上，对教材内容进行了重组，共设计了8个问题和2个例题，而且实现了问题的“生活化”．难度由低到高，形式由简洁直观到隐晦抽象，内容由数到形再到数．通过这些问题串，让学生们一起自然地建构新概念，应用新概念，反思新概念，从不同的角度理解新概念，最后提升到综合运用所学概念解决实际问题的思维水平，追求一种自然、流畅的教学节奏，取得良好的教学效果．

2.稚化教师思维，引领学生探究

现代认知心理学认为，新学习的知识必须纳入原有的认知体系，并在原有的认知结构中找到联系点，才能将新知识同化，牢固地掌握新知识．新课标提倡关注学生的认知特点，注意站在学生的角度，精心创设问题情景，诱发学生思维的积极性，用卓有成效的启发引导，促使学生的思维活动持续发展．备课首先应该备学生，教师应非常熟悉学生的知识基础和认知水平及学习的薄弱之处，要善于改变自己的身份，稚化自己的思维，把自己当做学生，从学生的角度审视问题，为学习者设计教学．要知道：在教师看来，清澈见底的问题到了学生那儿可能就是浑浊一片．本节课中的问题设计，坚持低起点，高落点，引导学生观察、归纳、验证，进行自主探究，激发学生的学习兴趣，培养锻炼了学生的思维能力．

3.及时调整预设，实现精彩生成

在新课程改革的教育理念下，数学课堂逐渐走向“学生参与、交往互动、共同发展”．课堂教学过程是一个个活泼的头脑在教师预设好的问题情境中的交流、对话与活动的过程，是“精心预设”与“动态生成”和谐统一的过程．课堂上，学生的深思顿悟、灵机一动、节外生枝和思维遇阻、疏忽大意等，都可能催生出一个个鲜活的教学资源，为创设智慧、高效的课堂带来可能．本节课中，笔者注意及时调整课前的预设，给学生创设了尽量多的发挥的空间，为积极的生成提供了丰富的可能性，让学生在自主学习的交流和互动中逐步完善认识，为丰富的生成提供了更大的空间，使课堂在师生的共同创造中变得充满灵性、充满智慧、充满活力．

1.章建跃.理解学生 理解数学 理解教学［J］.中国数学教育（高中版），2010（12）：1-5.

2．陈继理.“生”动的课堂才是高效的课堂［J］.中国数学教育（高中版），2012（1-2合刊）：43-45.

3．杨华文.看山还是山 看水还是水［J］.中学数学（高中版），2012（6）：16-18.