公式巧解涂色问题

☉江西省新干中学 胡勇彪

公式巧解涂色问题

☉江西省新干中学 胡勇彪

数列内容历来是高中数学课程的一个重点和难点，同时涂色问题也是近年高考，甚至竞赛的一个考试热点．通过对各种涂色问题的分析，不难发现它们之间存在着某种特定的规律，下面笔者就借助于数列的线性递推公式来巧解一类涂色问题．

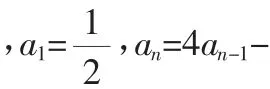
分析：题中所给出的数列递推公式，是一类形如an+1=pan+r·qn+m（p≠1，p≠0，r≠0，m≠0）型的线性递推公式，这种类型的数列通项一般利用待定系数法构造新的等比数列来解答，即可令an+1+x·qn+1+y=p（an+x·qn+y）化简，与已知递推公式对应比较，求出待定系数x和y，从而转化为新数列{an+x·qn+y}是公比为p的等比数列，进而可求出an.

［问题拓展］如图1，将一个圆环分成n（n≥2）个扇形区域，现用k（k≥2）种不同颜色对这n个区域染色，要求相邻区域颜色不同，问有多少种不同的染色方法.

解：用k种不同颜色对n个区域染色，记种数为an（n≥2，k≥2）.

A1有k种染法，A2有k-1种染法，…，An有k-1种染法（不论是否与A1同色），共有k（k-1）n-1种染法，但这k（k-1）n-1种染法分为两类：一类是An与A1不同色，另一类是An与A1同色，可看成An和A1合为一个区域，即an-1，an=（k－1）n+（－1）n（k－1）（n为区域数，k为颜色种数）.

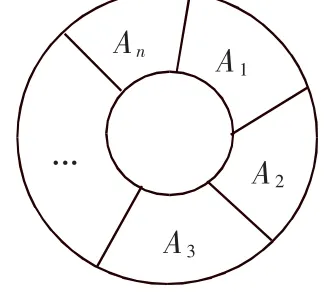
图1

［应用］

1.用红、黄、蓝、绿4种颜色给图2中的A、B、C、D4个小方格涂色（允许只用其中几种），使邻区（有公共边的小格）不同色，则不同的涂色方式有多少种？

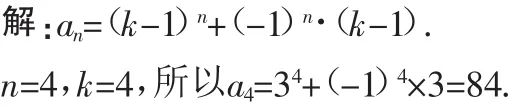
2.如图3，在一个正边形的6个区域中栽种观赏植物，要求同一区域中种同一种植物，相邻（有共同边）的2个区域种不同的植物，现有4种不同的植物可供选择，则共有（ ）种不同的栽种方案.

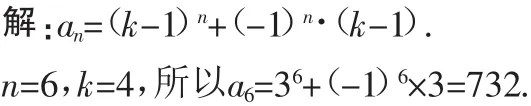
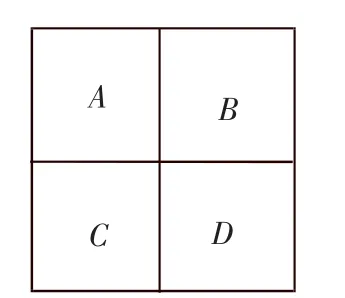
图2

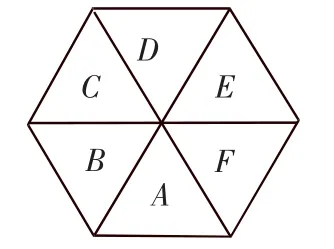
图3

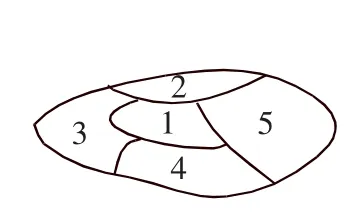
图4

3.如图4，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有_______种.（以数字作答）

解：对区域1着色：C14=4，然后再转化为用3种颜色对4个圆环区域（图5）的涂色问题．

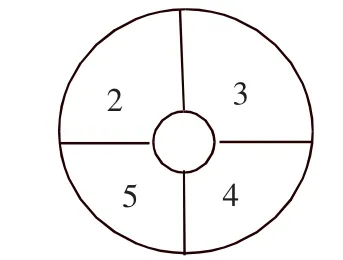
图5

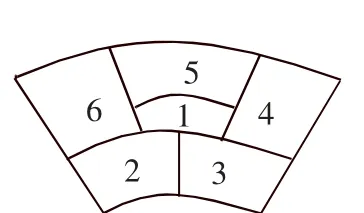
图6

4.（2003年全国卷理）某城市在中心广场建造一个花圃，花圃分为6个部分（如图6），现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有__________种.（以数字作答）

解：解题方法同第3题，共有120种.

5.用5种不同的颜色给图7中的“5角星”的5个顶点染色（每点染一色，有的颜色也可以不用），使每条线段上的两个顶点皆不同色，则不同的染色方法有_______种.

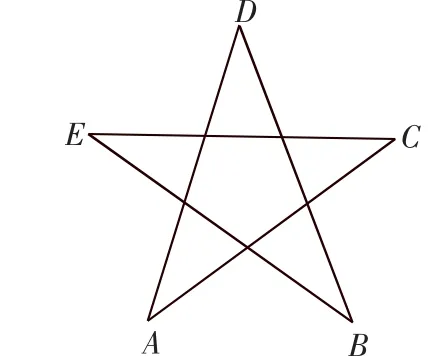
图7

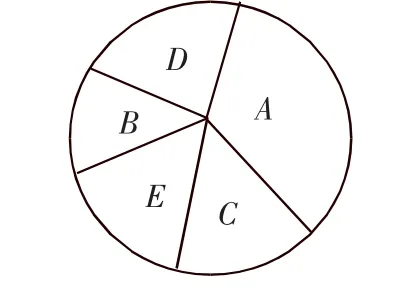
图8

解：问题转化为对图8所示的5个区域着色，要求相邻区域不同色.

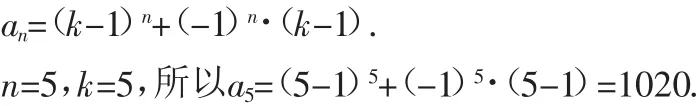
6.将一个四棱锥（如图9）的每个顶点染色，并使一条棱的两端异色，若只有4种颜色可供选择，则不同的染色方案有_______种.

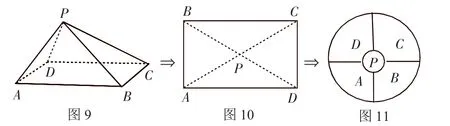
解：由题意可转化为图10并进而转化为图11所示的着色问题.

n=4，k=3，得a4=18.

所以染色方案共有：4×18=72（种）.