反思问题的分析与解题思路的形成

☉江苏省泗洪中学 彭晓珊

反思问题的分析与解题思路的形成

☉江苏省泗洪中学 彭晓珊

编者语：该文通过问题解决过程的反思这一方式让学生学会在解题中在分析问题的特征中寻找问题解决的途径，这对解题教学有借鉴意义.但要在反思的基础上能形成新的解法或发现解题规律.

从近年的高考数学试题来看，对能力的要求逐年提高，“题海战术”的功效明显下降，在教学中如何摆脱“题海战术”，提高数学素质，培养数学能力呢？这就要求在教学中教师应引导学生学会分析问题和解决问题，并从中发现问题解决的规律.本人试从一道试题的标准答案的分析来谈谈如何通过解题分析来获得问题解决的新视角，并从中提高学生的数学解题能力.

一、问题的提出

评析：这个解法运算正确，书写规范，过程完整，推理严密，还有没有更好的解决办法，还有反思的余地吗？下面我们不妨先研究一下解题步骤，是怎么解的，为什么这样解？

二、解题分析

1.题中主要抓住了三个主要问题依次来解决的

（1）求出u的值域.

（2）从f（u）=0的根u的范围来得到a、b所满足的条件.

（3）求出a2+b2的最小值.

2.解题步骤结构图

我们把整个问题的解决步骤简练地提炼出来，由这样一个解题步骤结构图：

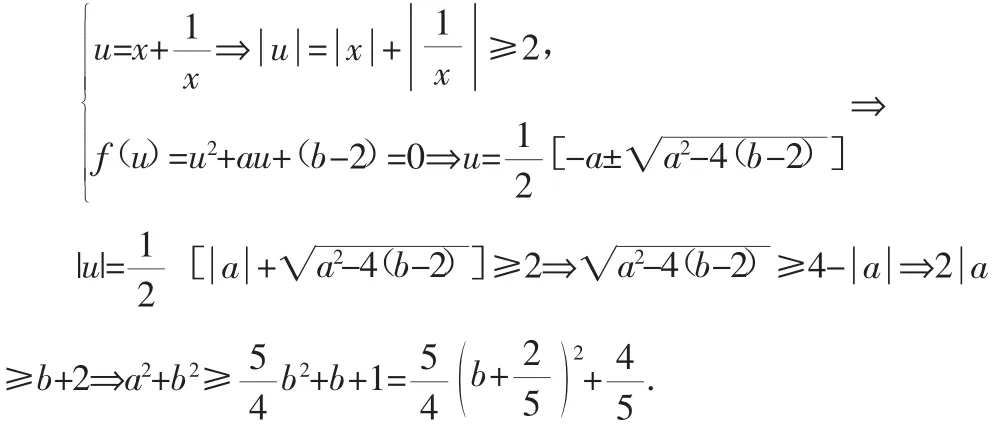
在这个解题步骤结构图中，我们可以清楚地知道在解这道题的过程中依次用到的知识为下面的框架图.

3.逻辑结构的初步分析

（1）在此解法中，利用f（u）=u2+au+（b－2）=0的根得到绝对值不等式，然后化为求解根式不等式是这道题目得以解决的关键.也是这道题的难点所在，一般而言作为学生是很难想到的.

（2）在这个答案中第二问的解决是起到桥梁的作用，是第一问和第三问的联系纽带.

（3）这道题目的标准答案是从正面入手，一环紧扣一环.

由以上初步分析知，对于上述的解决问题是循着先求u，然后求出a、b满足的不等式，最后求出a2+b2的最小值.这种思路是从正面入手，一环扣一环地得出最终结果.

三、题后反思

由以上初步分析知，对于上述的解决问题是循着先求u，然后求出a、b满足的不等式，最后求出a2+b2的最小值.这种思路是从正面入手，一环扣一环的得出最终结果.我们能否从其他角度入手，如反面考虑，换位思考.我们对每一步提出这样的想法：如果这一步不这样，那会是怎样？先进行如下反思.

1.反思问题的结构特征：

从上面的结构分析中可以看到，原解法中有三个未知数a、b、u，在原解法中突出了u的地位，强调了u的优先使用权，a、b退居二线，所以我就他们的地位不同得到下面的结构特征.

第一问的情况较简单，我们分析的重点放在第二问和第三问，在第二问的解决中始终围绕f（u）=u2+au+（b－2）=0至少有一实根，它的结构特征的探讨如下：

特征1：u2+au+（b－2）=0看成关于u的一元二次方程，在这里突出u的地位.

特征2：f（u）=u2+au+（b－2）看成二次函数y=f（u）与u轴的交点的个数至少有一个，这里还是突出u的地位.

特征3：u2+au+（b－2）=0看成一个恒等式问题，a、b、u，地位是相同的.

特征4：u2+au+（b－2）=0看成关于a、b的直线方程，把u看成常数，a、b地位突出.

与此同时，第三问a2+b2的最小值的解决办法将决定整个解题的方向，下面a2+b2的最小值就本题而言选取的策略如下：

a2+b2的最小值转化为二次函数问题来解决；

利用基本不等式来求解a2+b2的最小值；

利用a2+b2的几何意义来解决a2+b2的最小值.

在这里多种特征方式的出现，体现了知识间结构的清晰度和连通性，同时也开辟了解题途径的多样性，为我们下面的新解法做好基础性的铺垫.

2.反思资源利用

资源的利用是涉及到解题过程中的全过程和每一步，我们重点分析一下比较实质性的第二问的解决.

在第二问的解答的主要是找出根与系数的关系，这使得我们思考，除了这个关系外，还有其他的关系么，（特征2、3、4）其中哪一个关系对我们处理更加容易入手，我们有哪些资源可用，应该做怎样的安排？