三角形全等一则命题的新证

☉浙江省台州市黄岩区新前中学 汪嫣嫣

☉浙江省台州市黄岩区高桥中学 蔡历亮

三角形全等一则命题的新证

☉浙江省台州市黄岩区新前中学 汪嫣嫣

☉浙江省台州市黄岩区高桥中学 蔡历亮

文［1］呈现的课堂实录中有如下片断：

问题1：如图1，点D、E分别在线段AB、AC上，BE、CD相交于点O，AE=AD，要使△ABES△ACD，可以添加的一个条件是______.（请提供尽可能多的方法）

学生3（吞吞吐吐）：可以添加BO=CO.

教师：把你的证明思路说一下.

学生3：连接AO……不行，连接BC……也不行，看来证不了！

教师：证明需结合图形把条件与结论综合起来加以分析，有些条件看似可行，但从逻辑上并不一定行得通……

文［2］根据上述文本片断，给出了如下有关三角形全等的一个命题（以下简称命题［1］）：

如图1，点D、E分别在线段AB、AC上，BE、CD相交于点O，AE=AD，要使△ABES△ACD，可以添加的一个条件是BO=CO.

文［2］对命题［1］进行了证明，本文在此基础上，对证明的思路和过程进行了改进，不仅缩短了篇幅，而且更加易于理解，现呈现如下，供读者参考.

证明：连接DE，因AE=AD，所以△ADE是等腰三角形.过D作DM⊥AC，垂足为M；过E作EN⊥AB，垂足为N.当∠BAC是锐角时，线段DM、EN在△ADE的内部（如图2）；当∠BAC是直角时，线段DM、EN在△ADE的边上（如图3）；当∠BAC是钝角时，线段DM、EN在△ADE的外部（如图4）.不管哪一种情况，都有：

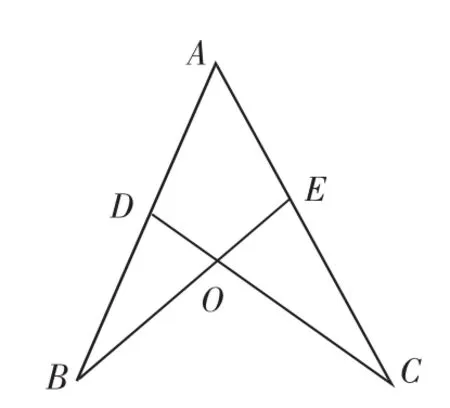
图1

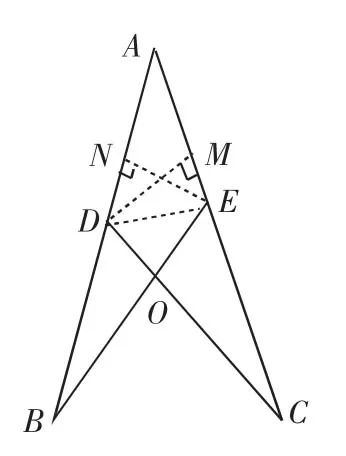
图2

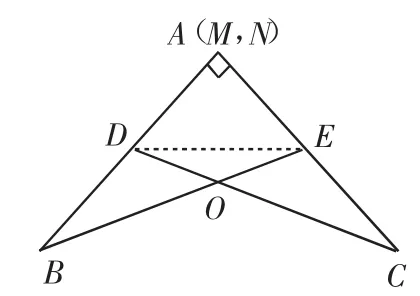
图3

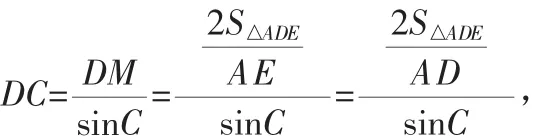
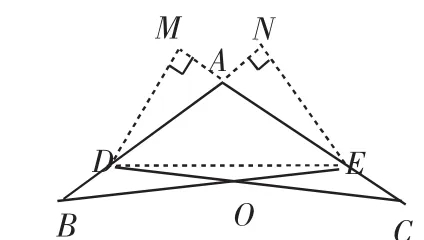
图4

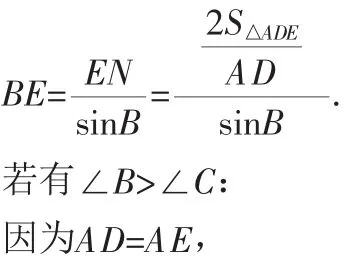
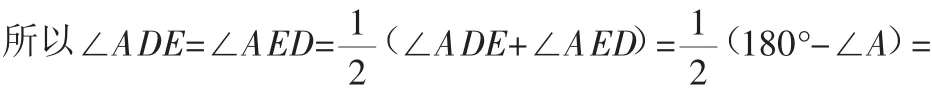
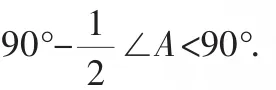
1.张宏政.一节“全等三角形复习课”的课例与说明［J］.中学数学教学参考（初中版），2011（3）.

2.任燕，蔡历亮，张智伟.一则教学片断引发的解题探究［J］.中学数学（初中版），2011（10）.