这样执著究竟为什么
☉江苏省南京金陵中学河西分校 李玉荣
这样执著究竟为什么
☉江苏省南京金陵中学河西分校 李玉荣
2012年湖北武汉市中考数学填空题第15题为:

图1
解:连接DC.
因为AE=3EC,△ADE的面积为3,所以△CDE的面积为1.
所以△ADC的面积为4.设A点坐标为(a,b),则AB=a,
OC=2AB=2a,而点D为OB的中点,
解完此题,笔者联想到2006~2011年湖北武汉市中考试卷,填空题的最后一题就是以反比例函数为背景命制.研究这些题的解法,不难发现:试题打破一贯单一的命题模式,立意高远,将几何图形自然地融入到反比例函数图像中,体现了数学内在的和谐、统一,凸显数形结合思想.关注过程与方法,考查学生可持续学习的能力,突出数学的思维价值,对于有效学习数学也有积极的启示,的确是高一级学校选拔学生的适宜考题.现结合这些试题进行分析,与大家分享.


图2
解:设A(x,y),作AB⊥x轴于点B,则AB=OB=x.

点评:此题由“反比例函数”+“线段长”组合命制,过图像上的点作坐标轴的垂线,将线段与坐标有机结合,利用勾股定理得解,难度适中.
2.3 并发症与复发情况对比 改良组的并发症发生率(2.4%)低于传统组(11.9%);传统组的复发率为16.7%,改良组的复发率为4.8%,改良组低于传统组;各组差异均显著(P<0.05)。见表3。
解:因为F是矩形OABC边AB的中点,

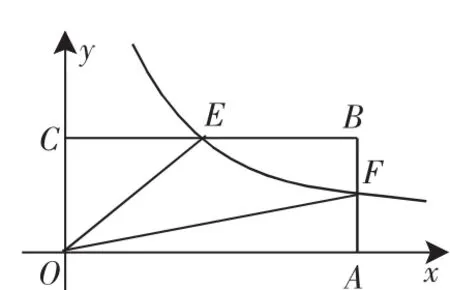
图3
点评:此题由“反比例函数”+“矩形”组合命制,将线段与坐标有机结合,利用“S=k”得解,难度适中.△
例3 (2008年)如图4,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=(x<0)的图像过点P,则k=______.

图4
解:连接PM,过点P作PH⊥y轴于点H,则MH=NH=3.

点评:此题由“反比例函数”+“圆”组合命制,过图像上的点作坐标轴的垂线,将线段与坐标有机结合,利用垂径定理及勾股定理得解,难度适中.


图5
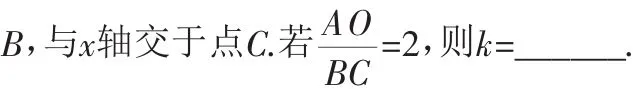
解:作BD⊥x轴于点D,AE⊥x轴于点E.

点评:此题由“反比例函数”+“平行线”组合命制,过图像上的点作坐标轴的垂线,将线段与坐标有机结合,利用相似三角形得解,难度教高.

图6

点评:此题由“反比例函数”+“线段积”组合命制,过图像上的点作坐标轴的垂线,将线段与坐标有机结合,利用一元二次方程根与系数的关系得解,难度颇高.
例6 (2011年)如图7,▱ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),顶点C,D在双曲线y=上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k=______.

图7
因为四边形BCDE的面积是△ABE面积的5倍,
所以▱ABCD的面积是△ABE面积的6倍.
又BC可看做AD向右平移1个单位,再向下平移2个单位得到,所以C(3,m-2).
点评:此题由“反比例函数”+“平行四边形”组合命制,过图像上的点作坐标轴的垂线,将线段与坐标有机结合,利用面积关系及相似三角形得解,难度颇高.
编者注:《函数》是初中数学的一个重要板块,主要包括一次函数、反比例函数、二次函数.相对而言,反比例函数比其他两种函数知识点少,图像又分布在两个象限且与坐标轴不相交,命题的思考空间似乎较狭窄,一般不受中考命题者的青睐.然而,武汉市却在中考填空题围绕“反比例函数”连续七年命制思维含量高、有创意的试题,这绝非易事,体现了命题者高超、精湛的技艺和功底,也为考生复习提供了明确而又广阔的空间,彰显了试题的人文关怀,2013年武汉市中考第16题,值得期待!
——《李叔同——弘一大师行踪图典》评介

