如何增强数学课前预习作业的有效性

☉江苏省海门市德胜中学 黄 华

如何增强数学课前预习作业的有效性

☉江苏省海门市德胜中学 黄 华

课前预习是学习过程中的一个重要环节，而作业是学生学习生活的重要组成部分.通过预习，学生可以了解学习内容的重难点，并有的放矢地进行学习.预习作业设计的质量高低，直接影响学生的学习兴趣和教学效果.但实践中，大多数教师对预习从思想上不重视，设计上不到位，往往流于形式，效果不明显，造成学生预习的主动性、积极性减弱.因此精心设计相应的预习作业显得尤为必要.以下就增强课前预习的有效性，谈谈自己对预习作业设计的几点想法.

一、预习作业的目标要明确

预习作业是巩固已学知识，对知识体系查漏补缺的同时，能够启迪学生对新知识、新方法的初步了解，逐步培养学生的自主学习能力.预习作业中设计每一个环节都应有明确的目标，即训

坛练什么，意在巩固哪些知识、初步形成哪些技能、了解哪些思想方法、哪些知识是重点、哪些知识点需加以综合、哪些知识点需加以提升等，教师要了然于心、目标明确，否则很容易形成无效预习.教师应根据《新课程标准》来确定预习作业的具体目标，要找准知识点的本质，不做漫无边际的训练，这样才能收到事半功倍的效果.

例如 人教版七年级数学“§3.1.1一元一次方程”的预习作业目标是：了解什么是方程，什么是一元一次方程；会将实际问题抽象为数学问题，通过列方程解决问题；能结合具体例子认识一元一次方程的定义，体会设未知数、列方程的过程，会用方程表示简单实际问题的相等关系；增强用数学的意识，激发学习数学的热情.

二、预习作业的体系要完善

预习作业要有整体性，是针对学科体系中涉及当前课堂教学中的重点知识和能力的准备训练.教师要根据《新课程标准》的总体要求，根据教材的重点和学生的实际，认真研究课时目标、单元目标及学科总目标，形成一个操作性强的目标训练体系.在这个训练体系中，准备训练是基础的训练，它是整个训练体系的目标能够顺利完成的保障.新授课的预习作业设计以简略复习已学知识和新知导入及简单运用为重点，单元复习课的预习作业设计应以在基础知识和基本能力的基础上，帮助学生建立起阶段性的知识体系为主要目的，而总复习的预习作业设计则在查漏补缺的基础上，以构建完整的学科知识体系为最高要求.

例如 第三章一元一次方程中第一部分的预习作业目标，让学生认识什么是方程，什么是一元一次方程，能结合具体例子体会设未知数、列方程的过程，会用方程表示简单实际问题的相等关系；而第二部分等式性质的预习作业目标，通过回顾小学已学的“等式性质”，自学初中的“等式性质”，并会用等式的性质解简单的一元一次方程；第三部分解一元一次方程的预习作业目标，在掌握了等式性质的基础上摸索一元一次方程的解法及步骤；第四部分实际问题与一元一次方程的预习作业目标类似于本章总复习目标，以方程为工具分析问题、解决问题（即建立方程模型），这也是本章的重难点所在.

三、预习作业的难度要适当

建构主义者认为，学生的学习有一个最近发展区，即对学生的学习应该提出一个适当的要求，这个适当的要求应该是适当高于但又不能过高于现有水平和能力，要求过高或过低，学习的效果都不理想.

例如 在作业中设计这样的训练：1.小红将自己的年龄乘3减5，得数为31，则小红的年龄为＿＿__岁；2.已知方程（m-2）x|m-1|+4=7是关于x的一元一次方程，则m=____.对于学生来说前者显然太简单，学生仅用小学知识也完全可以解决，低估了学生的能力；而后者考查知识点较多，大部分学生会顾此失彼，错误率高，这样又会打击学生学习的积极性.像这种题目可将其分解训练，如：a.（m-2）x+4=7为关于x的一元一次方程，则m=____；b.x|m-1|+4=7为一元一次方程，则m=____.

设计预习作业要循序渐进，要体现出梯度，这样才能提高学生自主探究的热情，达到有效预习的目的.

四、预习作业的方式要多样

预习作业需要教师依据课程标准来精心设计，防止繁、难、偏、怪的题目或题型出现.对于难点，可通过判断、选择等题型进行有针对性的练习；重点知识可通过一题多解、一题多变等题型进行强化训练.从训练的形式看，既有独立完成，又有讨论、探究等.同时，预习作业要符合学生的兴趣特点和注意特点，注意激发兴趣，防止死记硬背、机械重复的训练方式.

例如 “§3.1.1一元一次方程”的预习作业：

（Ⅰ）充分预习教材第102-104页的内容，找出本课的主要内容，并作上记号，提出自己的疑惑和困难，提交小组解决，未能解决的提交作好记录，提交全班讨论.

（Ⅱ）完成下列问题（独立思考后，与同桌交流）.

1.判断下列各式哪些是方程，哪些不是方程.

2.请你写出一个你喜欢的一元一次方程是________.

A.0 B．1 C．2 D.3

4．根据下列题意，设未知数，列出方程：

①小明年龄的3倍比他的爸爸的年龄多2岁，小明爸爸今年40岁，问：小明几岁？

②某校女生人数是全体学生数的52%，比男生多80人，这个学校有多少学生？

这样的作业设计，将知识目标细化、问题化，将知识点、主要数学思想、方法融入设计的问题中．学生在探索、回答设计的问题时，既激活了思维，又增加了求知欲，同时又培养了创造力和合作意识．

五、预习作业的过程要富有启发性

预习作业设计时应注意题目形式的新颖性和创造性，要富有创意，有助于充分调动学生的思维，激发学生的兴趣，同时要注重新旧知识的对比和迁移，注重活学活用知识，有效地提高学生的能力.在作业设计过程中，教师一定要有意识地组织设计探索题，促进发现、类比、总结和反思等思维活动，引导他们探索发现数学规律，总结提炼数学的思想方法与策略，使学生不断受到启迪，从而达到增强能力和发展智力的目的.

例如 “§3.1.2等式的性质”的预习设计：

（Ⅰ）回顾小学已学的“等式性质”.

1．读一读：小学解方程的方法和依据．

解方程：2x－22=64.

解：2x－22＋22=64＋22（等式两边加同一个数22，结果仍相等）；

2x=86；

2x÷2=86÷2（等式两边除以同一个数2，结果仍相等）；

x=43.

检验一下，上述结果是否正确？写出你的检验过程.

2．写一写：小学解方程的依据是“等式性质”，请把它写出来.

3．做一做：用小学学过的“等式性质”解下列方程：

（1）x－2=3；（2）2x=4．

提醒：（1）如果忘了，请看看小学六年级上的课本或问问同学！

（2）初中很多内容与小学类似，要认真体会，并积累这种“类比”或“新旧对比”的学习方法！

（Ⅱ）自学初中的“等式性质”

1．读一读：带着下列问题阅读“书本第82-84页内容”.

（1）“等式性质”是怎么发现或得到的？用简要的语言归纳.

（2）“等式性质”的具体内容是什么？用红笔在书中画出，并背出.

2．比一比：初中的“等式性质”和小学的“等式性质”在表述上有什么不同？

3．想一想：下列变形的依据是什么？

（1）从a＋3=b＋3，得到a=b.这是根据等式性质1，等式两边______，结果仍相等.

（2）从－2a=－2b，得到a=b.这是根据______，_____，______.

（3）请你再举两个类似的变形，并说明变形的依据.

4．做一做：利用等式的性质解方程.先阅读第83页例2，再模仿其解题的过程，解下列方程：

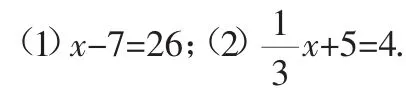
这样的预习设计一方面使预习内容问题化、具体化，增强了预习的目的性，便于学生阅读时集中注意力，增强思维量，能有效地提高学生独立思考和独立探索的能力，培养学生自主学习，获取知识的习惯，有利于学生在听课过程中把握重点和难点，为参与课堂教学、提高学习接受度打下基础.另一方面人与人的友情提醒拉近了师生之间的距离，激发学生充满自信，充满热情地学习数学，变“要我学”为“我要学”.

六、预习作业的讲评要适时和到位

在预习作业实施的过程中，讲评环节非常重要，预习作业讲评与试卷讲评不同，既需要教师在课前充分考虑到学生在训练的过程中可能出现的各种问题和应对方面，更需要教师在训练过程中密切关注学生，及时准确地捕获训练中出现的各种信息，发现学生存在事先没有预料到的新问题，这些新问题需要教师在很短的时间内作出判断和分析，通过讲评给学生一个准确的结论，这对教师的专业水平提出了更高的要求.预习作业的讲评，还要把握好讲评的时机和尺度.

一般来说，还可以将讲评贯穿在师生共同讨论的过程中，及时纠正学生不正确的认识和思维方式.讲评的语言要准确，讲评的内容要精练，要在充分肯定学生成绩的基础上，用简洁的语言指出训练中的问题所在，并且帮助学生分析问题存在的原因，避免类似问题的再次出现.对于学生在训练过程中的有创意的见解要予以充分的肯定.教师通过讲评引导学生对知识体系加以归纳和总结，举一反三，帮助学生掌握本质和规律.

俗话说：“精彩的背后必然有艰苦卓绝的准备与付出.”预习正是为学生们精彩绝伦的展示提供了充分的准备，更使他们懂得了“凡事预则立，不预则废”的含义.学生学会预习，形成了良好的习惯，就意味着掌握了自学方法，为更好地学好数学奠定了扎实的基础.

1.全日制义务教学数学课程标准解读.北京：北京师范大学出版社，2002：41-52.

2.章飞.数学教学设计的理论与实践.南京：南京大学出版社，2009：61-86.

3.徐强.让数学预习充满活力.中学数学教学参考，2010（1-2）：29-30.