盘点有关折叠问题

☉河南省滑县枣村中心学校 李玉春

盘点有关折叠问题

☉河南省滑县枣村中心学校 李玉春

折叠问题在近几年的中考中屡屡出现，试题灵活多变，用以考查学生的抽象思维能力，已成为中考题型的一朵奇葩，而有些同学解题时感到十分困惑.其实折叠的图形基本上就是我们学过的一些特殊图形如：直角三角形、平行四边形、矩形.涉及的知识点无非就是全等形、对称、勾股定理等.要想快速、准确地解决有关折叠的问题，我认为应注意以下几个方面.

一、注意分析题中折叠前后的变量与不变量，特别是不变量

例1（2012年江苏宿迁市）如图1，将一张矩形纸片ABCD沿EF折叠，使顶点C，D分别落在点C′，D′处，C′E交AF于点G. 若∠CEF=70°，则∠GFD′=______°.

解题思路：先根据“两直线平行，内错角相等”求出∠GFE的大小，再利用“两直线平行，同旁内角互补”求出∠DFE的大小，然后根据折叠后图形的形状与大小没有改变，得到∠EFD′的大小，最后利用角的差的意义即可解答.

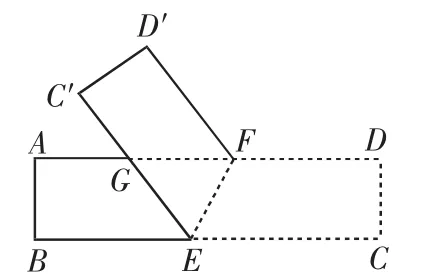
图1

解答过程：因为四边形ABCD是矩形，

所以AD∥BC.

所以∠GFE=CEF=70°，∠CEF+∠EFD=180°.

所以∠EFD=110°.

由折叠可知∠EFD′=∠EFD=110°，

故∠GFD′=∠EFD′－∠GFE=110°－70°=40°.

所以答案为40.

点评：本题的命制为了降低难度，将问题改为求角度，这就大大地方便了考生最短时间内快速求解，这也能算得上是命题的一种新的尝试.

二、要注意利用对称性寻求等量关系，注意矩形与直角三角形中直角的条件，计算时可用勾股定理寻求数量关系

例2（2012年福建南平市）如图2，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，则EF的长为（ ）.

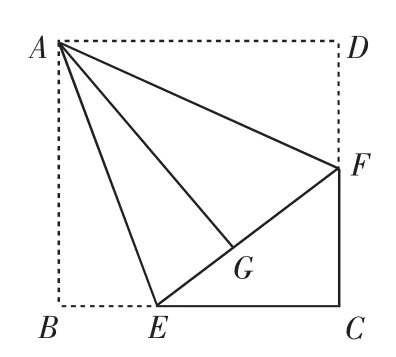
图2

解题思路：由折叠可知EF=BE+DF.设DF为x，用x的式子表示出EF和CF，然后在Rt△EFC中根据勾股定理列出方程，解之即可.

解答过程：因为折叠，所以EG=BE=1，FG=DF.

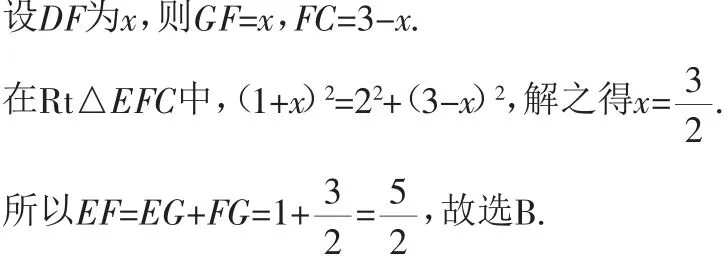
点评：折叠后图形的形状与大小没有改变，这是解决本题的关键所在.另外，如何综合地利用所学勾股定理求相关的线段的长度是正确解答的基础.

三、注意发现图中的全等图形，利用全等图形的性质提供某些条件用来解题

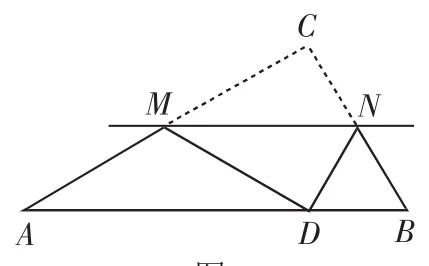
图3

例3 （2012年四川资阳市）如图3，在△ABC中，∠C=90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC=6，NC=2，则四边形MABN的面积是（ ）.

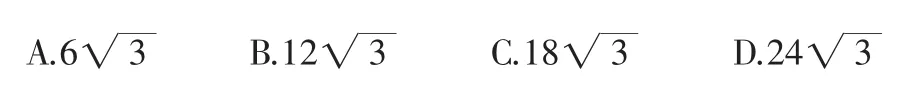
解题思路：四边形MABN的面积=△ABC的面积-△CMN的面积.

规律总结：将△ABC沿直线MN翻折后可得到全等图形，灵活运用△ABC的中位线的性质得到边与边之间的关系.

例4 （2012年湖北荆门市）如图4，已知正方形ABCD的对角线长为2，将正方形ABCD沿直线EF折叠，则图中阴影部分的周长为（ ）.

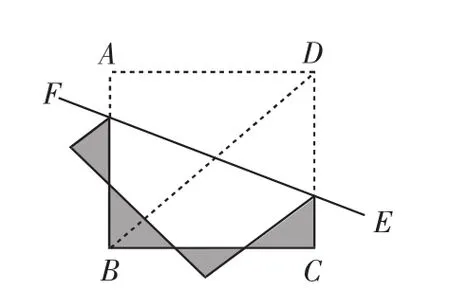
图4

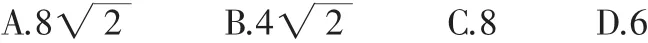
解题思路：图中阴影部分由四个三角形组成，其周长由两部分组成，一部分是直线EF下方的正方形边长的一部分，另一部分是直线EF上方的正方形边长折叠后的部分.这两部分的和正好是正方形的周长.

答案：C

点评：折叠前后的图形是全等图形.把分散的集中、零碎的凑整，用整体的方法思考问题.

总之，通常情况下，考查折叠知识都是利用矩形的折叠，求相关线段的长度，利用到勾股定理、方程等知识.解决折叠问题，关键是抓住以下几点：（1）抓住折叠本质：①折起部分与重合部分是全等的；②点与点重合产生垂直平分线，线与线重合产生角平分线.（2）结合三角形全等、勾股定理，设出恰当的未知数，运用勾股定理解决.