数学学科中如何灵活运用各种数学思想方法解题

☉江苏省赣榆县实验中学 高 稳

数学学科中如何灵活运用各种数学思想方法解题

☉江苏省赣榆县实验中学 高 稳

数学作为对客观事物的一种认识，与其他科学认识一样，其认识的发生和发展过程遵循实践——认识——再实践的认识路线.但是，数学对象（量）的特殊性和抽象性，又产生与其他科学不同的、特有的认识方法和理论形式.由此产生数学认识论的特有问题.数学知识由经验知识形态上升为理论形态后，数学家又把它应用于实践，解决实践中的问题，在应用中检验理论自身的真理性，并且加以完善和发展.

在解决数学问题时，要能够灵活运用各种数学思想方法，并且在学习和探究过程中，要善于归纳总结，并且还要有所创新.著名的数学家，莫斯科大学教授C.A.雅洁卡娅曾在一次向数学奥林匹克参赛者发表《什么叫解题》的演讲时提出：“解题就是把要解题转化为已经解过的题.”数学的解题过程，就是从未知向已知、从复杂到简单的化归转换过程.

一、转化思想

我们在解题中的困难，一般来说，都是或由于这个问题比较复杂，或由于这个问题不太熟悉.当你遇到较复杂或者你从未见过的一些题目时，一定别害怕，仔细分析，往往能把问题转化成另一种你所熟知的问题，变换其叙述的方式，或改变思考的角度，或把它转化成另一种你所熟悉的问题，从而使问题获得解决，这种思考方法，我们称之为转化思想.

分析：先解方程组求x、y（用含m的代数式表示），再根据－1＜x－y≤2建立关于m的不等式，求其解集.

点拨：解不等式（组）的依据是不等式的性质1、2，另外，要注意不等式与不等式组的转化.

二、数形结合思想

就是通过“数”与“形”之间的对应、转化来解决数学问题的思想.所谓“数”，就是指数或式，所谓“形”，就是指图形或图像.“数”与“形”之间互相依存，对应：“数”是“形”的抽象和概括，“形”是“数”的几何表现.同时，在一定的条件下，它们又可以互相转化：“数”借助于图形的性质，可以使许多抽象的概念和数量关系直接化、形象化、简单化，而“形”的问题经过数量化处理，并借助于计算，可以使较深的问题归结为较容易处理的数量关系来研究.

例2 实数a、b在数轴上对应点的位置如图1所示，则一定有（ ）.

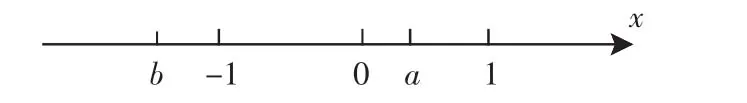
图1

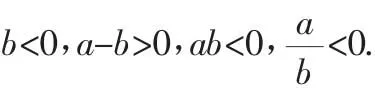
答案：D.

点拨：正确地从数轴上获取实数a、b的大小范围是解题的关键.

三、类比思想

分析：可先求出不等式组的解集，再由x=1是不等式的解，利用不等式组的解的定义，列出关于a的不等式组求解.还可以根据不等式组解的意义，类比方程解的意义，直接将x=1代入不等式组中，直接求解关于a的不等式组.

因为x=1是原不等式组的解，即不等式组有解，所以－6a－3＜x≤－2a+5.

点拨：通过类比不仅可以发现新旧知识的不同点和相同点，还有助于利用已有知识去认识并加深理解新知识.

四、数学建模思想

近几年来中考中常出现与“日常生活”有关的决策及最佳答案选择性试题，解决此类问题的关键是在理解题意的基础上，建立与其相应的“数学模型”——不等式（组）的相关知识，确定问题的答案.

例4 某航空公司规定：旅客可随身带一定重量的行李，如果超过规定的重量，那么需要购买行李票，行李票费用y（元）是行李重量x（kg）的一次函数，其图像如图2所示.

图2

（1）求y与x之间的函数关系式.

（2）求旅客最多可免费携带行李的重量.

（3）某旅游团的旅客所买的行李票的费用在4至15元之间，求旅客所带行李重量的范围.

分析：先观察函数图像经过哪些特殊的点，然后设出y与x之间的函数关系式y=kx+b，联立方程组求出k、b的值.

解：（1）观察函数图像可知，直线经过（40，6）和（60，10）两点.

解得k=0.2，b=－2，所以y与x之间的函数关系式为y=0.2x－2.

（2）由 y=0，得 x=10.

所以旅客最多可免费携带行李10kg.

所以旅客所带行李的重量范围是30～85kg.

点拨：“三个一次”之间有着密切的联系，由一次函数图像上的点列方程组可得到一次函数关系式，通过构建不等式组又可以求出所带行李重量的范围.总之，通过建立函数、方程、不等式（组）等数学模型解决实际问题是非常重要的，在今后的学习中一定要掌握其要领.