如何提高学生有理数的运算能力

☉江苏省盐城市盐都区实验学校 刘连冬

如何提高学生有理数的运算能力

☉江苏省盐城市盐都区实验学校 刘连冬

提高有理数的运算能力是学好数学的基础.提高有理数的运算能力，就是要求能准确、简捷地进行运算.正确理解概念，掌握运算法则，明确相关概念，运用转化的思想方法，准确、合理、熟悉地运用运算法则和运算律是提高运算能力的关键.

一、掌握法则是提高运算能力的关键

要学好有理数的运算，首先要抓好运算符号.这是区别于小学运算的关键.如，有理数加法法则：同号两数相加，取相同的符号，并把绝对值相加；绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；一个数同零相加，仍得这个数.在运用这个法则进行运算时，首先要看清符号，其次运用好法则.

正确的掌握运算法则，要抓住加法和乘法两种关键的运算，注意把减法和除法向它们进行转化（即：减去一个数，等于加上它的相反数；除以一个数，等于乘以这个数的倒数），如果不考虑转化的条件，往往会导致错误.

二、小数和分数混合运算中要进行适当的转化

在小数和分数混合运算中，往往需要把小数化成分数或把分数化成小数，成为同一种形式，运算起来才比较方便.在解题前要有一个观察、比较的过程，怎样做更简单、易行就采用哪种方法做，不要勉强固定于某一种形式.需要化成哪种形式，需要针对题目中的数的特点来决定.

三、巧用运算律是提高运算能力的重要途径

在有理数的运算过程中，往往会运用到结合律、分配律.如果在运算中能巧用运算律也是提高运算能力的一个重要途径.对于运算律的使用，不仅要学会正向使用，也要学会逆向使用.比如分配律：a（b+c）=ab+ac，由左向右为正向使用，由右向左是逆向使用.

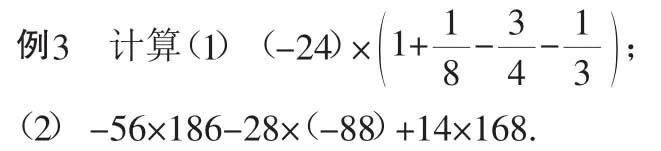
通过观察，第（1）题括号内的分数，它的分母是8、4、3，分别是24的约数，那么就可以直接利用分配律.第（2）题如果直接运算，运算量就比较大，通过观察发现，28和56有关系，14和56也有关系，也就是说28×2=56，14×4=56，将原式化为－56×186+56×44+56×42，再利用乘法分配律进一步化为－56（186－44－42），最后得到结果－5600.这样解题就快得多了.所以，认真观察题目的结构，注意各个因数之间的关系，有积极使用运算律的意识，就可以使运算变得非常巧妙.

四、注意运算的顺序

在许多运算中，往往会发现在复杂运算中会出现大括号、中括号、小括号，有加法、减法、乘法、除法，在这样比较复杂的四则运算中，除了要注意正确运用运算法则和运算律外，还要注意运算的顺序.即先做第三级运算乘方，再做第二级运算乘、除，再做第一级运算加、减，在有括号的式子当中，先做括号里边的运算，一般按照从小括号、中括号、大括号的顺序进行.在同级运算中，按照从左到右的顺序依次进行.在具体的运用中要结合运算法则和运算律进行灵活的运用.

五、注意挖掘隐含条件

当遇到有一定综合性问题时，就需要引导学生注意挖掘题目提供给我们的隐含条件，创造可解的条件来求解.

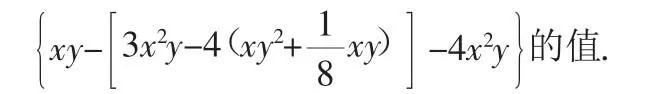
求一个代数式的值，就要知道代数式中字母的值，本题中并没有直接给出出x、y的值，通过审题，发现|x+2|与（y-1）2都是一个非负数，并且|x+2|与（y-1）2互为相反数，由互为相反数的定义可以得到，|x+2|+（y-1）2=0，然后利用非负数的性质，得到x=-2，y=1.这样就创造了代入求值的条件.

综上所述，在进行有理数的运算中，只要注意正确运用法则进行计算，抓住运算律，注意运算的顺序，在整式运算中注意去括号法则的正确运用，在处理综合问题的时候注意挖掘隐含条件，就能使学生的运算能力得到提高，为今后的学习打下扎实的基础.