如何解决几何动点型问题
☉江苏省盱眙县第二中学 庄亿农
如何解决几何动点型问题
☉江苏省盱眙县第二中学 庄亿农
动点型问题就是在三角形、矩形、梯形等一些几何图形上,设计一个或几个动点,并对这些点在运动变化的过程中相伴随着的等量关系、变量关系、图形的特殊状态、图形间的特殊关系进行研究考查.常见的动点型问题有单动点型和多动点型两类.当一个问题是求有关图形的变量之间关系时,通常建立函数模型或不等式模型求解;当求图形之间的特殊位置关系和一些特殊的值时,通常建立方程模型去求解.

图1
一、单动点型
例1 已知,如图1,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系,A,B,C三点的坐标分别为A(8,0),B(8,10),C(0,4),点D为线段BC的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为t秒.
(1)求直线BC的解析式.
(2)若动点P在线段OA上移动,当t为何值时,四边形OPDC的面积是梯形COAB面积的?
(3)动点P从点O出发,沿折线OABD的路线移动过程中,设△OPD的面积为S,请直接写出S与t的函数关系式,并指出自变量t的取值范围.

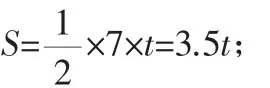
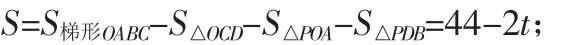
当动点P在线段BD上运动时,即18≤t<23时(可以用勾股定理求出BD=5),△OPD的面积S=S△OPC-S△OCD=-1.6t+36.8.

点评:这是一道以直角坐标系为载体,通过一个动点在直角梯形边上的运动,构成面积与图形的形状问题,主要考查了矩形的性质、勾股定理等有关知识.
二、双动点型
例2 如图2,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.
(1)求梯形ABCD的面积.
(2)当PQ∥AB时,P点离开D点的时间等于多少秒?
(3)当P,Q,C三点构成直角三角形时,P点离开D点多少时间?
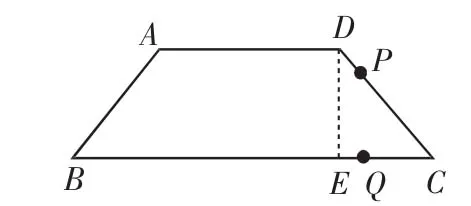
图2

图3

(3)当P,Q,C三点构成直角三角形时,有两种情况:
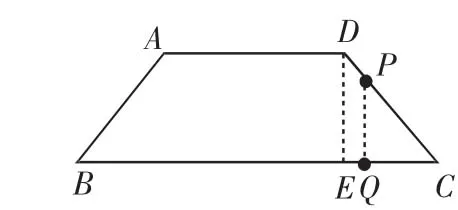
图4
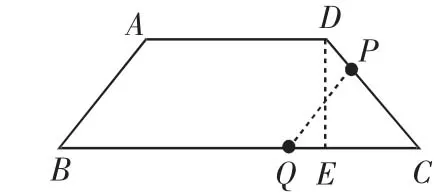
图5

点评:解有两个动点的运动型问题,先弄清楚两个动点各自运动的出发点、路线、终点以及运动的速度和时间,然后在假设两个动点在某处不动的情况下,对图形进行分析与探究,利用所学数学知识求解.

