运用数学思想巧做因式分解问题

☉江苏省建湖县实验初级中学教育集团 朱 霞

运用数学思想巧做因式分解问题

☉江苏省建湖县实验初级中学教育集团 朱 霞

学习数学不仅是学习知识和提高能力，更是让学生真正理解数学知识与技能、思想和方法，用数学思想指导知识的应用和能力的提升.掌握数学思想，就能很好地解决因式分解，快捷地解题计算.

一、类比思想，触类旁通

如果把整数120进行因数分解就是4×5×6，与之相类似的是a2－b2就是（（a+b）和（a－b）的相乘的结果.因此，多项式a2－b2就可以分解为（a+b）（a－b），由此可知（a+b）和（a－b）皆为a2－b2的因式.如此进行类比，不仅很容易就让学生理解因式分解的意义，而且为因式分解的方法提供了思路，真正是由此及彼，类比晓理.

例1 不用计算器快速算出20122-20112的值.

分析：这是比较大的数字，如果直接平方计算也能算出，但很复杂；如果细看，发现这是完全平方公式的数学应用.a2-b2=（a+b）（a-b），且2012-2011=1很特殊.

分析：这个也是比较大的数字，如果一个一个计算用计算器也很麻烦，但是如果根据学习的因式分解就可以方便快捷的做出来，把99999看做一个公因式提取出来，且剩下的因式相加正好是个整数.

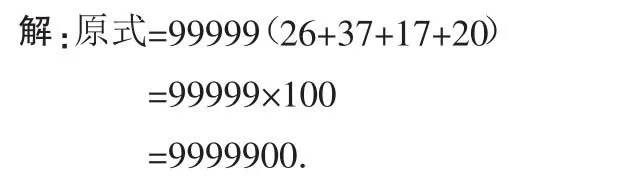
点评：学会了类比思想来分解因式，不仅能很好的理解和掌握知识，而且能提高做题速度和能力，能够让学生触类旁通，培养学生的创新思维.从而很好地完成学生对因式分解概念的迁移，能够准确分辨出因数分解与因式分解的异同，触类旁通，举一反三，真正理解因式分解的概念.

二、分类思想，有序别类

例3 因式分解8ax－4ay+2bx－by.

分析：可以把8ax、-4ay，2bx与－by各分一组或者把8ax、2bx，－4ay、－by各分为一组.

例4 对多项式9m2－6m－4n2+1进行因式分解.

分析：可以把9m2、－6m与1这三个分成一组，把－4n2单列为一组，运用完全平方公式和平方差公式.

点评：运用这类思想一定要有全局意识，分组别类因式分解一定要有前瞻性，要有一双火眼金睛，准确快速的把多项式的各个项进行分类，然后进行合理地分组，从而让分解过程更为简捷，达到因式分解的目的.

三、转化思想，化繁为简

例5 对9x2+6x-3进行因式分解.

分析：一般的方法是提取公因式3，但是提取后不能进一步分解，如果根据9x2+6x是完全平方式的前两项，再加一个1，把-3变成1-4就可以变成完全平方，再进行平方差分解就可以进一步分解.这就是转化思想的魅力体现.

分析：根据多项的特点，可以先用分类思想进行分类，然后根据分类特点构建平方公式进行转化，把3转化成4-1.

点评：解决数学因式分解的习题应该具有转化思想，在保证整体不变的情况下，对多项式进行有效变形转化，把整个多项式转化为我们非常熟悉的容易操作的形式.因式分解，能够很好地解决一般方法很难解决的试题，能够快速地算题解题.

四、整体思想，局部换元

例7 因式分解（a2+a）2-14（a2+a）+24.

分析：先把a2+a看做一个整体，用换元法置换.设a2+a=m，然后变成新的简单多项式，再置换原式.

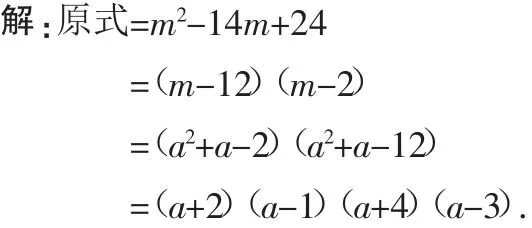
点评：这是最简单的运用整体思想局部换元，一看便知把a2+a当做一个整体.还有一些整体现象不明显时，还应进一步转化再进行整体思想局部换元.

例8 把（a2-2a）2-2a（2-a）+1分解因式.

分析：这个多项式中，没有很明显的局部整体，需要进一步转化，然后在整体换元.此题要先将-2a（2-a）化为2（a2-2a），然后将（a2-2a）作为一个整体，运用完全平方公式分解.

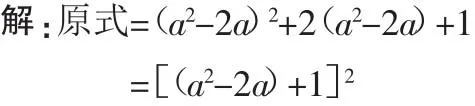
谋

例9 把4x（x-y）2-12xy（y-x）分解因式.

分析：先把-12xy（y-x）化为12xy（x-y），再把公因式4x（x-y）看作一个整体，运用提公因式法分解.

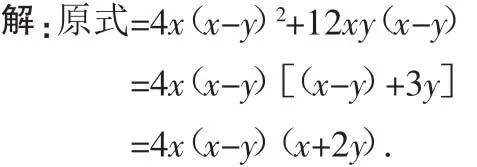
点评：上述例题的解决，是整体思想的运用，让看似难解的问题变得容易，让看似烦琐的试题变得简洁.做因式分解这类试题应具备这种宏观和整体思想，要能从宏观审视，再从细节入手，整体把握，局部优化.尤其对于结构较为复杂难辨的多项式进行分解，如果把某些局部看做整体处理，多项式的结构就会更加简洁明朗，问题由繁变简，很容易进行因式分解，这就是整体思想.

总之，数学学习是掌握知识，迁移能力，更应该感受数学思想.学会运用数学思想巧做因式分解，能够很好地培养发散性思维、灵活思维；在快速准确做题的过程中，培养思维的深刻性、抽象性；在已学知识的基础上，对知识进行归纳总结，不断优化思维品质，培养思维的严谨性、批判性.