一类走走停停行程问题的解答

☉浙江省宁波大学理学院数学系 赵玉春 陈 旻

一类走走停停行程问题的解答

☉浙江省宁波大学理学院数学系 赵玉春 陈 旻

本文讲述了走走停停行程问题中，每行进固定的距离两人就休息相同的时间而产生的追及问题的解法，并把它推广为两人休息时间点不同的一类题的解法.

行程问题 走走停停问题带余除法

一、引言

行程问题是研究物体运动的，它研究的是物体的速度、时间、行程三者之间的关系.行程问题是反映物体匀速运动的应用题.行程问题涉及的变化较多，有的涉及一个物体的运动，有的涉及两个物体的运动，有的涉及三个物体的运动.涉及两个物体运动的，又有“相向运动”（相遇问题）、“同向运动”（追及问题）和“相背运动”（相离问题）三种情况.但归纳起来，不管是“一个物体的运动”还是“两个物体的运动”，不管是“相向运动”、“同向运动”，还是“相背运动”，它们的特点是一样的，具体地说，就是它们反映出来的数量关系是相同的，都可以归纳为三个基本公式：速度×时间＝路程；路程÷时间＝速度；路程÷速度＝时间.而走走停停是一类行程问题的总括，这类行程问题一般是两人在绕着某一环形跑道（包括三角形、四边形等）运动，每人走一定的时间就休息一定的时间或者在环形跑道上的固定点休息（耽搁）一定的时间，而由此产生的追及问题.追及的地点可以相同，也可以不同，但方向一般是相同的.由于速度不同，所以就发生了快的追上慢的问题.对于行程问题，已有不少人进行了研究，但专一研究走走停停问题的人却不是很多.因此我们对两人在某一环形跑道上的固定点休息一定的时间的这类走走停停行程问题进行了研究，并以公式的形式详细给了出来.

二、例题

关于两人在某一环形跑道上的固定点休息一定的时间的走走停停行程问题，我们把它分成了两类：休息时间相同；休息时间不同.对于每一种情况，我们先给出公式的形式，再以具体的例子加以详细介绍.

1.休息时间相同

设甲、乙两人分别从A、B两地同时同向出发，A、B两地相距n0S0，甲、乙两人的速度分别为V甲、V乙（V甲＞V乙），且每行S0就停下来休息t0时间.求甲第一次追上乙需要多久.

分析：这里分三种情况讨论，讨论顺序如下：

①在乙休息结束的时候追上，此时甲比乙多休息时间为（n0－1）t0.

②在乙休息过程中且没有结束时追上，此时甲比乙多休息时间在（n0－1）t0～n0t0.

③在行进过程中追上，此时甲比乙多休息时间为n0t0.

下面来看r与t0之间的关系：

例1 环形跑道周长是800米，甲、乙二人按顺时针方向沿环形跑道同时同地起跑，甲每分钟跑100米，乙每分钟跑80米，甲、乙两人每跑200米均要停下来休息一分钟，那么甲首次追上乙需要多少分钟？

解：这就相当于乙在甲前方800处，两人同时向前跑.于是就有S0=200米，n0=4，t0=1分钟，V甲=100米/分，V乙=80米/分.

2.休息时间不同

解：首先，考虑是不是在乙休息结束的时候追上，

下面来看r与t乙之间的关系.

若0＜r＜t乙，则说明是在乙休息过程中且没有休息结束时追上的.

若r=0，则说明是在乙刚好要休息时追上的.

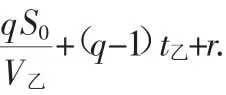
若r＞t乙，则说明是在行进中追上的.设此时乙所行走的路程为S，

例2 甲、乙两只蜗牛沿着一个边长为12厘米的正方形ABCD爬行，甲蜗牛每秒行3厘米，每次转弯的时候要停2秒，乙蜗牛每秒行2厘米，而每次转弯要停1秒，现在甲位于A点，乙位于D点，同时顺时针方向爬行.请问甲蜗牛第一次追上乙蜗牛所用的时间.（A、B、C、D逆时针排列）

解：这里S0=12厘米，n0=1，V甲=3厘米/秒，t甲=2秒，V乙=2厘米/秒，t乙=1秒.

三、小结

这类问题一直是困扰学生的难题.对于这一类型的题目，我们该如何下手呢？我们先以公式化的形式给出了具体的模型，然后再以具体的例题给以详细的讲解和说明，相信读者已经明白，解题关键是抓住题目中所蕴涵的等量关系，再根据最基本的关系式（路程=速度×时间；路程÷时间=速度；路程÷速度=时间）以及时间差的等量关系，从而使问题简单化.

1.黄佳琴.中小学数学竞赛中的行程问题［J］.科技信息，2010（129+145）.

2.孙国柱.谈行程问题的类型及其解法［J］.赤峰教育学院学报，2000（03）.

3.陈世洪.合理转化条件巧解行程问题［J］.良师，2004（Z2）.

4.韩东民.解行程问题易出现的错解［J］.良师，2004（Z2）.

5.董仁福.一道有趣的行程问题［J］.中学生数学，2005（10）.

6.颜伏刚.两种方法巧解行程问题［J］.语数外学习（初中版八年级），2007（01）.

7.王维荣.列方程解行程问题例析［J］.数理化学习（初中版），2006（12）.

8.廖帝学.解析多解行程问题［J］.时代数学学习（七年级），2004（Z1）.