梯形问题中如何添加辅助线

☉湖北省襄阳市第二十八中学 米伶俐

用简单已知的图形去探索较复杂未知的图形，是我们学习平面几何的重要和基本的方法.大多数梯形问题都需要添加辅助线.总的来说，梯形问题就是通过添加辅助线，把梯形转化为平行四边形和三角形，然后把问题放在平行四边形和三角形中来解决.下面简单介绍一下梯形常见辅助线添加的方法.

一、平移梯形的腰

1.平移一腰，把两腰和上底、下底的差放在一个三角形中.

例1 如图1，在梯形ABCD中，AD∥BC，AD=1，BC=4，∠C=70°，∠B=40°.

则AB的长为.

分析：过点A作AE∥DC，交BC于点E，得平行四边形AECD和△ABE，这样，上下底之差和同一底上的两个角就集中在一个三角形内，从而求解.

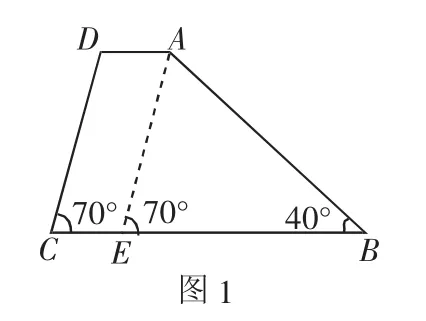
解：过点A作AE∥DC，交BC于点E，得平行四边形AECD和△ABE.

因为AE∥DC，所以∠AEB=∠C=70°.又因为∠B=40°，所以∠BAE=70°.所以△BAE为等腰三角形.

所以AB=BE=BC-CE=BC-AD=4-1=3.

2.同时平移两腰，构建新的特殊三角形.

例2 如图2，在梯形ABCD中，AD∥BC，E、F分别为AD、BC的中点，若∠B+∠C=90°，AD=7，BC=15，求EF的长.

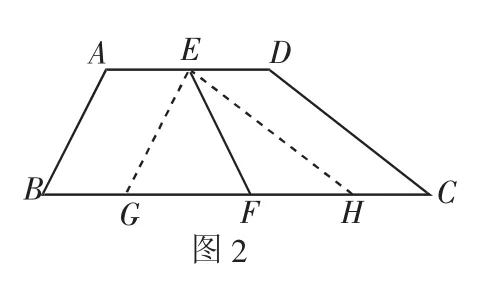
解析：已知条件中有同一底上的两个角∠B+∠C=90°，充分利用这一条件，把它放在一个三角形中，构成直角三角形，而EF恰为直角三角形的中线，可以利用直角三角形斜边上中线等于斜边长度的一半，求出EF的长.

解：过E作EG∥AB，EH∥DC，分别交BC于G、H，得平行四边形ABGE和平行四边形DCHE.

因为∠B+∠C=90°，所以∠EGH+∠EHG=90°.

所以△EGH为直角三角形.因为E、F分别为AD、BC的中点，所以GF=FH，即F为Rt△EGH斜边上的中点.因为GH=BC-AD=15-7=8，所以

小结：只要已知梯形中两腰、两底的长，同一底上的两个角大小等条件，加上平移一腰或两腰后构成的三角形是等腰、等边或者直角三角形这些条件，就可以把梯形问题转化为三角形问题.

二、平移对角线

过梯形的上底的一个端点作一对角线的平行线，与另一底的延长线相交，得平行四边形和三角形，再利用平行四边形和三角形的有关性质解题.

例3 如图3，在梯形ABCD中，AD∥BC，AC⊥BD于O，AC=6，BD=8，求梯形ABCD的高.

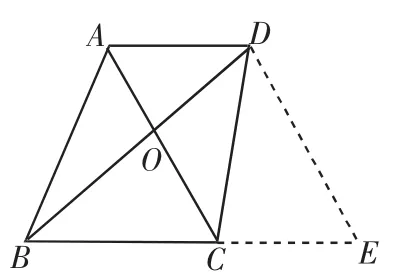
图3

解：设梯形ABCD的高为h，过D点作DE∥AC，交BC的延长线于E，得平行四边形ADEC，所以DE=AC=6.因为AC⊥BD，DE∥AC，所以∠BDE=90°.在Rt△BDE中，BD=8，DE=6，所以BE=10.因为即8×6=10h，所以h=4.8，即梯形ABCD的高为4.8.

小结：在梯形问题中，只要有两条对角线的大小和位置关系的条件，就用平移一条对角线的办法，把两条对角线、上下底之和放在一个三角形中，就会出现等腰三角形、等边三角形、直角三角形、等腰直角三角形等特殊三角形，就可以利用特殊三角形的性质来解决此类问题.

三、过梯形一腰中点构造全等三角形

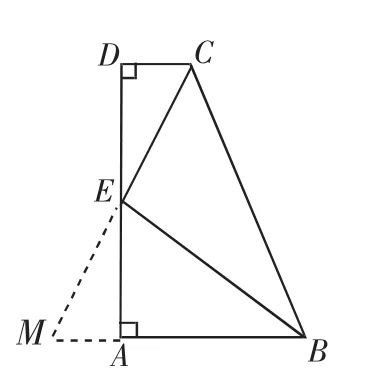
图4

找出一腰中点，连接顶点和这个中点并延长，与底边延长线相交，构造全等三角形.

例4 如图4，在梯形ABCD中，AB∥DC，∠A=90°，AB=2，BC=3，CD=1，E是AD的中点，求证：CE⊥BE.

证明：延长CE交BA的延长线于点M.

因为E是AD的中点，所以AE=DE.

又因为∠BAE=∠CDE=∠MAE=90°，∠MEA=∠CED，

所以△MAE≌△CDE.

所以ME=CE，AM=DC.

所以BM=AB+AM=2+1=3.又因为BC=3，

所以△BCM为等腰三角形.又因为ME=CE，所以BE⊥CM，即CE⊥BE.

小结：在梯形中，只要有腰上的中点，采用过中点构造全等三角形，从而把上下底之和与另一条腰集中在一个三角形中，而这个三角形又是一个特殊三角形，问题就简单了.

四、作梯形的高

过梯形较短的底的两端点向另一底所在直线作垂线，把梯形分割成两个直角三角形和一个矩形.

例5 在梯形ABCD中，DC∥AB，AD=BC，若AD=5，CD=2，AB=8，求梯形ABCD的面积.

解：通过作高DE、CF，把这个梯形分割成两个全等的直角三角形和一个矩形，从而求出AE=3，利用勾股定理可以得出DE=4，也就是梯形的高.这道题就迎刃而解了.本题解法省略.

另外，我们还可以采用延长梯形的两腰，构建两个三角形的方法解决一些实际问题.总之，通过添加梯形的辅助线，我们就能化繁为简，轻松解决很多梯形问题.