反比例函数的“特殊性质”及应用

☉江苏省泗洪县 潘茜银

一、典型例题分析

分析：图中△MON是以图像上一点和过这点作x轴的垂线所得的垂足及坐标原点围成，只需根据三角形面积公式就可以求出k的值.

可得|k|=4.

所以k=±4（k=4不合题意，舍去）.

即k=－4.

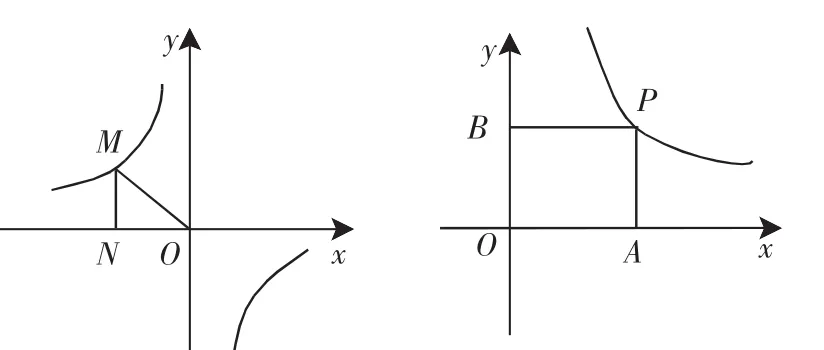
图1图2

解析：本题只是把图1中的三角形变为矩形，易知：

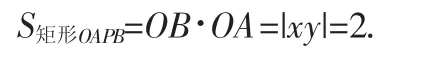
二、综合例题分析

例3 （浙江省湖州市）已知：在矩形AOBC中，OB＝4，OA＝3，分别以OB、OA所在直线为x轴和y轴，建立如图3所示的平面直角坐标系，F是边BC上的一个动点（不与B、C重合），过F点的反比例函数的图像与AC边交于点E.如果记S＝S△OEF－S△ECF，求当k为何值时，S有最大值，最大值为多少？

解法一：如图3，设E（x1，y1），F（x2，y2），△AOE和△FOB的面积为S1、S2.

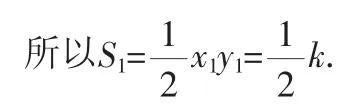
所以S1＝S2，即△AOE和△FOB的面积相等.

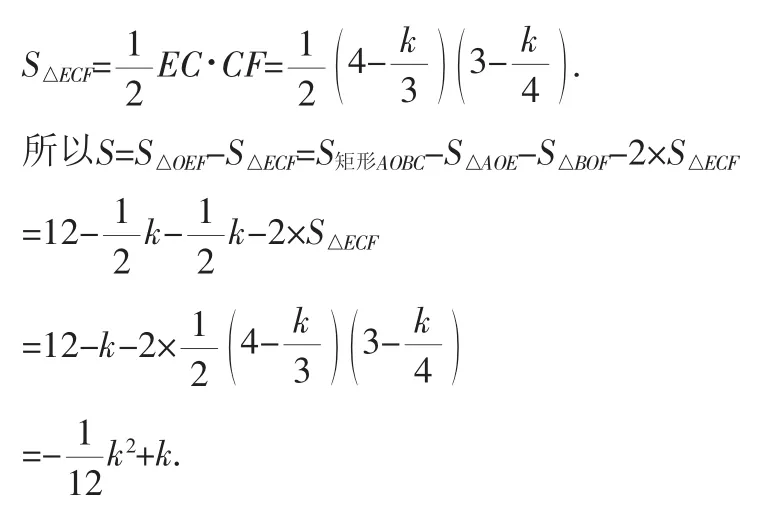
故S为关于k的二次函数，当k=6时，S有最大值为3.

图3 图4

本题也可以利用矩形的对称性及反比例函数中的面积相等的三角形进行转换，将不规则图形的面积转化为易求的规则图形面积，使学生的思维得以升华.

解法二：如图4，过E点作EM⊥x轴交与M点，作FN⊥EM交与N点.

由题意易得，四边形AOME、四边形ENFC、四边形NMBF都为矩形.

因此，S为关于k的二次函数，当k=6时，S有最大值为3.