加速度计/磁强计无陀螺捷联惯导姿态解算研究

渠 晋， 宋艳君， 臧 洁， 程洪炳

(空军工程大学工程学院自动控制工程系，西安 710038)

0 引言

无陀螺捷联惯导系统(Gyro-Free Strap-Down Inertial Navigation Systems，GFSINS)与普通捷联惯导系统相比具有低成本、低功耗、可靠性高、寿命时间长等优点，但由于在GFSINS中，载体的角速度是通过加速度计的比力方程解算得到，而目前加速度计测量误差较大，造成姿态角计算值的误差积累速度较快［1］。近年来，多传感器数据融合技术发展迅速，在各个领域都得到了广泛的应用，本文利用了GFSINS和三轴磁强计构成组合导航系统，以磁强计的测量值结合国际地磁场模型修正GFSINS的姿态角误差，抑制误差的积累，提高了姿态角的解算精度。

1 GFSINS姿态角解算

角速度计输出方程［2］为

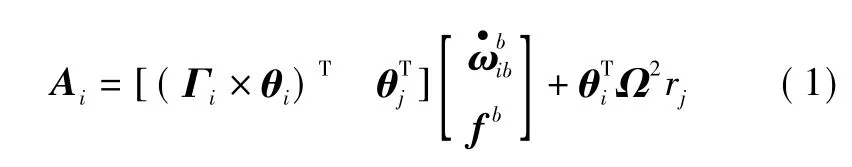
其中:i为惯性系;b为载体系;ri为加速度计安装位置矢量;θi为敏感方向矢量;fb为投影到载体系的比力;为载体角速度为载体角加速度;Ω为载体角速度的反对称矩阵［2－3］。

因此得到固连在载体上的N个加速度计输出的矩阵形式为

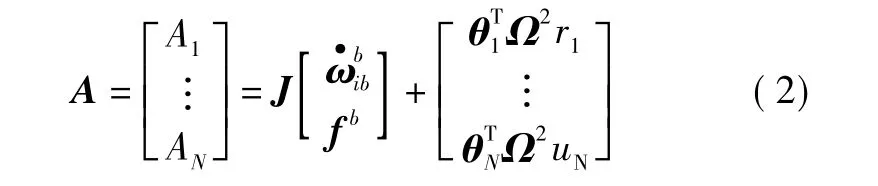
令Q为J的左逆矩阵，则有

由式(3)可计算得到载体相对惯性空间的角速度在载体系3个轴的分量，进而可以确定载体姿态角。

2 加速度计配置方案

目前常用的配置方案有六加速度计和九加速度计，相比于六加速度计，九加速度计配置方案系统可靠性更高，而且可以利用冗余信息提高角速度解算精度。本文采用如图1所示的九加速度计配置方案［4］。

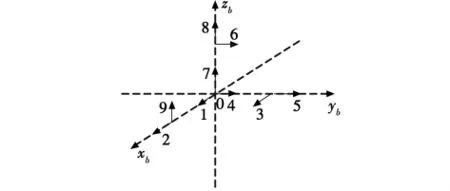
图1 加速度计配置方案Fig.1 Configuration of the accelerometer

原点在载体质心处，yb轴沿载体纵轴并指向载体弹头，xb轴沿尾翼并与yb轴垂直，zb轴与xb，yb轴构成右手坐标系，加速度计安装位置如图1所示，箭头所指方向为加速度计的敏感方向。

加速度计的位置矢量r和敏感方向矢量θ为

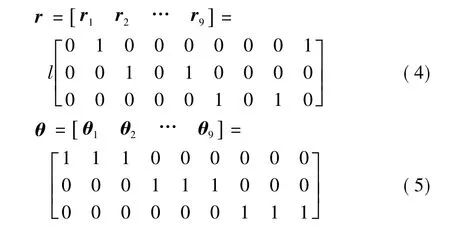
式中，l为非原心处加速度计与原心之间的距离。由公式(2)得加速度计的输出方程为

对照组采取常规治疗，根据实际病情予以对症干预，使用钙离子拮抗剂、β受体阻滞剂、硝酸酯类药物等，阿司匹林口服剂量为100 mg/次，1次/d，曲美他嗪20 mg/次，3次/d，单硝酸异山梨酯注射液剂量为40 mg/次，1次/d，静脉注射，将其置于生理盐水中使用，阿托伐他汀20 mg/次，1次/d，治疗时间为两周。

其中:ωx，ωy，ωz为载体角速度在载体系各轴上的分量;在载体系各轴上的分量;ωxωy，ωxωz，ωyωz为冗余信息。由式(6)解得

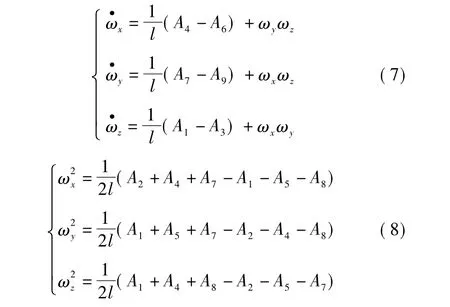
载体角速度的计算值选取式(8)开方得到的数值，并利用式(7)确定开方后的符号，即(以x方向为例)

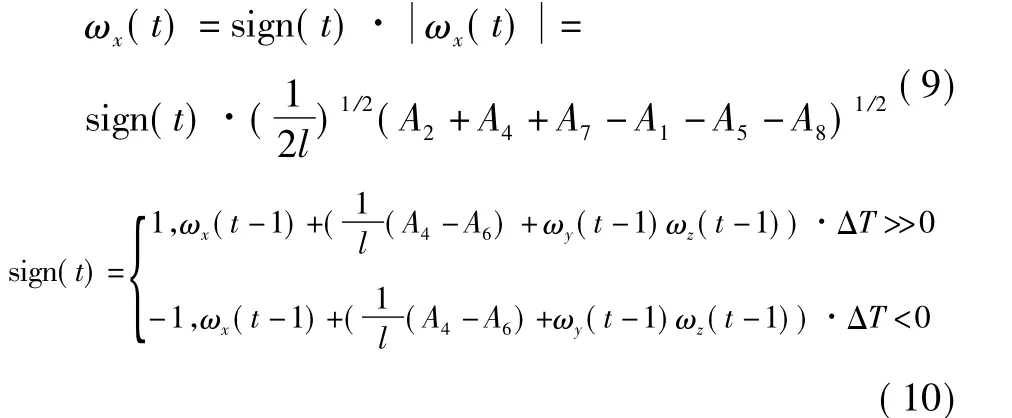
由式(9)得到了角速度，经过积分即可获得姿态角(以俯仰角φ为例)

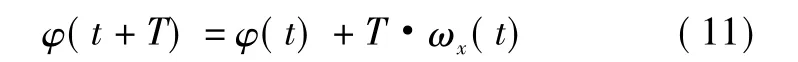
式中，T为计算周期。

由于加速度计存在测量误差，通过积分得到姿态角的误差随时间快速积累，不利于姿态角的精确解算。

3 加速度计/磁强计的滤波方程

无陀螺惯导系统姿态角的数值积分中存在累积误差等因素，这使得计算得到的姿态角误差不断积累。磁强计具有抗摇动与抗震性，在现代导航系统中常结合加速度计来提供辅助的航向信息，其提供的航向精度高且稳定，因而广泛地应用于无人机、航空、航天自主导航领域。本文在系统中增加了三轴磁强计，通过测量地磁场在载体系3个轴向的分量，修正姿态角。本文采用了国际地磁场模型［6］，假设地球是一个半径为RE的标准球体。采用当地地理坐标系来描述磁场强度，则可得到沿坐标系3个方向的磁场分量为［6－7］

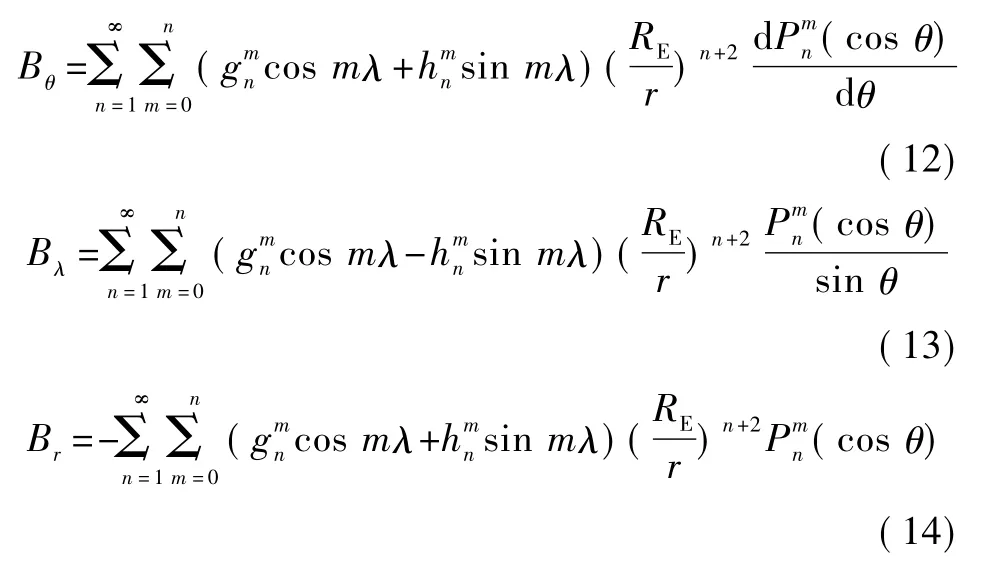
式中:r为地心距;RE为地球平均半径;λ为经度;θ为余纬;为n次m阶缔合勒让德函数;为基本磁场的高斯系数。

根据国际地磁场模型，可以得出当地地磁场强度。将此磁场强度和三轴磁强计测量值的差值作为观测值，就建立起了磁场强度的差值和四元数误差的关系，对误差四元数进行反馈校正，从而实现动态条件下的姿态确定。

系统姿态误差方程［8－9］为

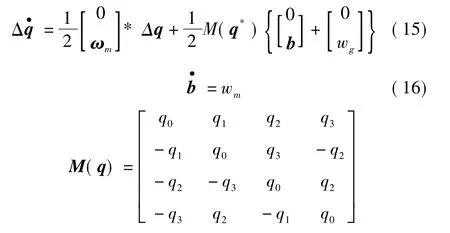
式中:ωm是载体坐标系相对于地理坐标系的转动角速度;q是测量的姿态四元数;b是加速度计的零偏误差;wg是加速度计的测量噪声;wm是加速度计的零偏误差。

取状态变量X=［Δq b］T，则系统状态方程为

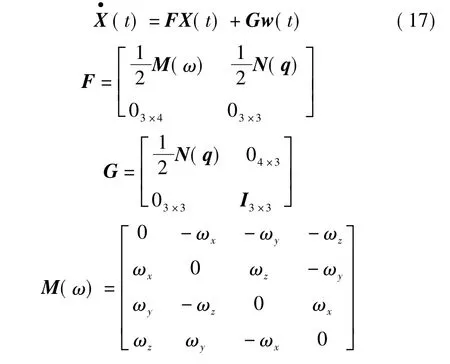
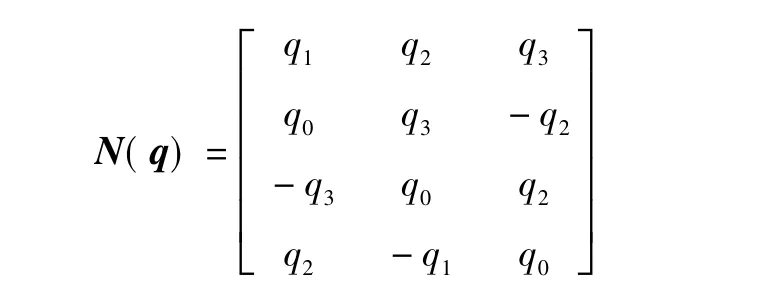
式中:Δq=［Δq0Δq1Δq2Δq3］T;b=［bxbybz］T;w(t)=［wgwm］T。

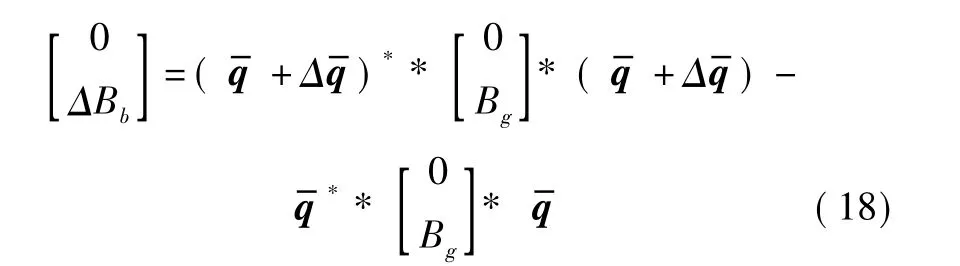
对式(18)进行展开可得系统观测方程

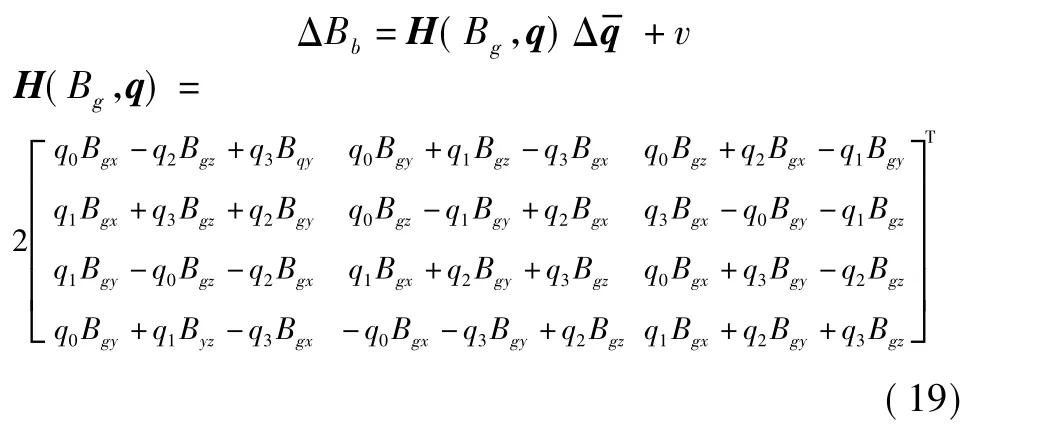
由式(17)、式(19)通过Kalman滤波得到误差四元数的估计值，则真实的四元数为误差四元数与测量的四元数 q 的和［4］，即

根据载体四元数即可计算得到载体姿态角。

4 仿真结果

利用某型导弹的弹道数据，分别在有磁强计辅助和无磁强计辅助的情况下进行仿真实验，配置方案的参数设计为:加速度计的精度为10－6g;磁强计的精度为 ±0.5°;加速度计安装位置 l为 0.1 m，仿真步长为1 s，仿真时间为350 s。初始位置设计为北纬40°、东经120°、海拔高度500 m;导弹初始速度为500 m/s，初始俯仰角45°，航向角30°。仿真结果如图2～图5所示。

从仿真结果可以看出，无磁强计辅助GFSINS的姿态角度误差在很短的时间内就急剧发散，而磁强计辅助无陀螺系统的解算结果相对比较稳定。对有无磁强计辅助解算出的姿态角误差进行统计分析发现，在仿真时间段内，无磁强计辅助GFSINS的俯仰角解算误差均值为0.0932，方差为0.0115，横滚角解算误差均值为 －0.0966，方差为0.0116;磁强计辅助 GFSINS 的俯仰角解算误差为0.0011，方差为0.0021，横滚角解算误差为0.0089，方差为0.0041。这表明磁强计辅助GFSINS可以明显提升姿态解算精度。

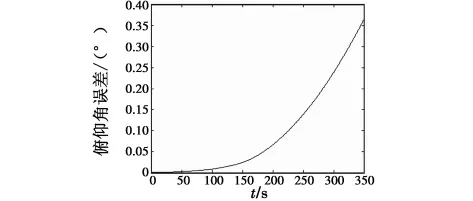
图2 无磁强计辅助GFSINS的俯仰角误差Fig.2 Pitch error of GFSINS without magnetometer aiding

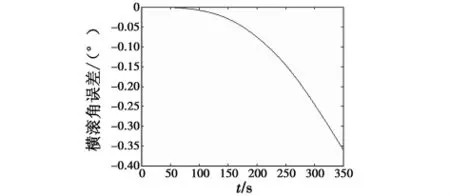
图3 无磁强计辅助GFSINS的横滚角误差Fig.3 Roll error of GFSINS without magnetometer aiding

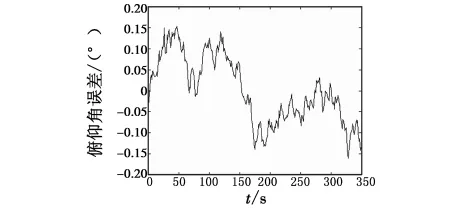
图4 磁强计辅助GFSINS的俯仰角误差Fig.4 Pitch error of GFSINS with magnetometer aiding

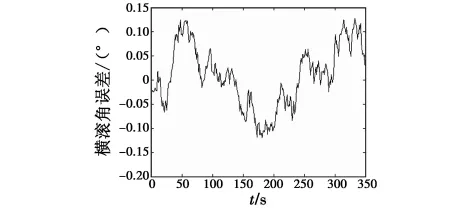
图5 磁强计辅助GFSINS的横滚角误差Fig.5 Roll error of GFSINS with magnetometer aiding

5 结论

在GFSINS中，构造了一种改进的九加速度计配置方案，该配置能直接得到载体的角加速度项和角速度乘积项。由于加速度计测量误差的存在，角速度误差随时间快速积累，所得的姿态角误差值也出现强烈的离散现象。将磁强计用于辅助GFSINS姿态解算中，用得到的地磁场载体系轴向分量和当地国际地磁场模型3个轴向地磁场分量的差值修正姿态误差角，有效避免了加速度计的测量误差引起的积分误差积累，提高了GFSINS姿态解算的精度。

［1］ 史震，于秀萍.无陀螺捷联式惯性导航系统［M］.哈尔滨:哈尔滨工程大学出版社，2007.

［2］ TAN C W，PARK S，MOSTOV K，et al.Dsign of gyroscope-free navigation systems［C］//2001 IEEE Intelligent Transportation Systems Conference，August 2001:25-29.

［3］ EGZIABHER D G.A gyro-free quaternion-based attitude determination system suitable for implementation using low cost sensors［C］//2000 IEE Position Location and Navigation Symposium，2000:185-192.

［4］ 赵国荣，陈穆清.一种用于九加速度计GFSINS的姿态角速度辅助算法［J］.系统仿真学报，2007，19(14):3350-3353.

［5］ HUANG Lin，JING Wuxing.Attitude-independent geomagnetic navigation using onboard complete three-axis magnetometer calibration［C］//2008 IEEE Aerospace Conference，2008:1-7.

［6］ 杨晓东，王炜.地磁导航原理［M］.北京:国防工业出版社，2009.

［7］ 董昆，周军，葛致磊.基于地磁场的新型导航方法研究［J］.火力与指挥控制，2009，34(3):153-155.

［8］ 杨功流，李士心，姜朝宇.地磁辅助惯性导航系统的数据融合算法［J］.中国惯性技术学报，2007，5(1):46-49.

［9］ 穆华，任治新，胡小平，等.船用惯性/地磁导航系统信息融合策略与性能［J］.中国惯性技术学报，2007，15(3):322-326.

［10］ 田菁，吴美平，胡小平.三轴磁强计姿态确定［J］.国防科技大学学报，2001(5):17-21.

［11］ 韦娟，宁方立.误差四元数及其在航天器姿态控制中的应用［J］.飞行力学，2006，24(2):60-62.

［12］ 秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1998.