利用导数求函数的极值(最值)的几个特例
☉江苏省连云港高级中学 高 原
函数的导数,作为一种工具,被引入到我们的新教材中.它的一个重要的作用就是求函数的极值(最值),但是在利用它求极值(最值)时,往往有很多的误区,现总结如下.
特例1 设x0是函数y=f(x) 的极值点,则下列说法正确的是( ).
A.必有f′(x0)=0B.f′(x0)不存在
C.f′(x0)=0或f′(x0)不存在D.f′(x0)存在但可能不为0
答案:C
解析:函数f(x)=x3,f ′(x)=3x2,f ′(0)=3×02=0,但x∈(-∞,0)时,f′(x)>0;x∈(0,+∞)时,f′(x)>0,故尽管有f′(0)=0,但0不是函数的极值点.
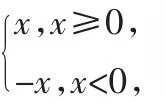
评注:x0是函数的极值点是f′(x0)=0的既不充分也不必要的条件,即x0是函数的极值点时,有f ′(x0)=0或f ′(x0)不存在;当f ′(x0)=0时,x0也不一定是函数的极值点.
特例2 设函数f(x)=(x3-1)2+1,下列结论正确的是( ).
A.x=1是函数的极小值点,x=0是极大值点
B.x=1及x=0均是函数的极大值点
C.x=1及x=0均是函数的极小值点
D.x=1是函数的极小值点,函数无极大值点
答案:D
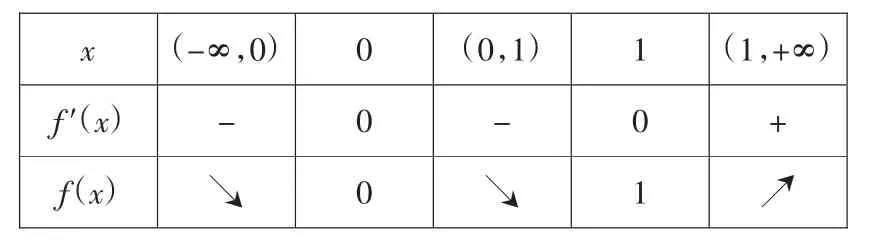
解析:令f′(x)=6(x3-1)x2=0,解得x1=0,x2=1.列出表格如下:
即当x∈(-∞,0)时,f′(x)<0,x∈(0,1)时,f′(x)<0;x∈(1,+∞)时,f′(x)>0,所以函数在x=1处取得极小值,无最大值.
评注:我们在利用函数的导数求函数的最值时,一定要认真观察函数在各段上导数的符号,从而准确判断各段上函数的单调性,确定函数的极值和最值.
特例3 函数f(x)=x(x-1)(x-2)(x-3)…(x-50)在x=0点处的导数为( ).
A.0 B.502C.100 D.50!
答案:D
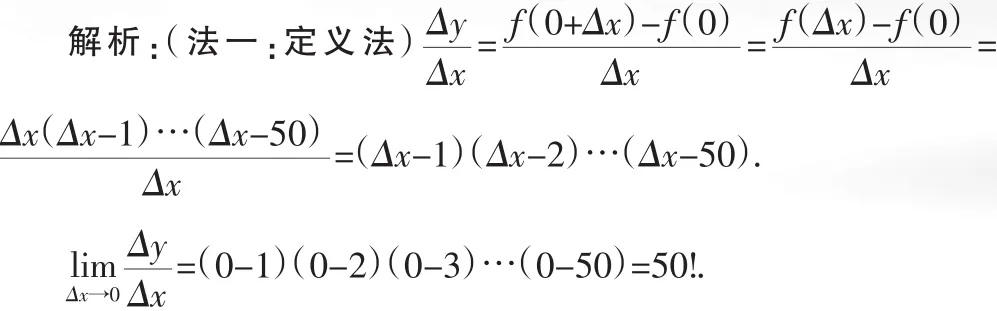
(法二:导数的积运算)f(x)=x·[(x-1)(x-2)…(x-50)].
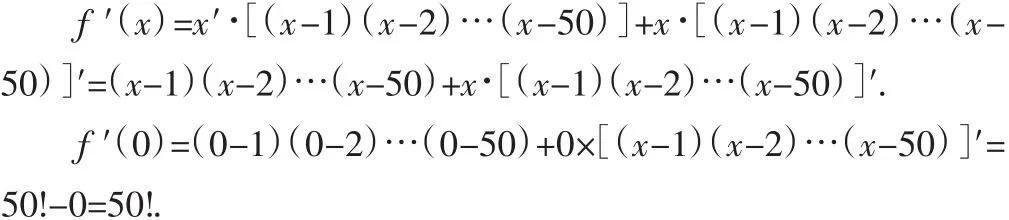
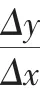
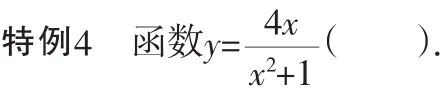
A.有最大值2,无最小值 B.无最大值,有最小值-2
C.最大值2,最小值-2 D.无最值
答案:C

当x=0时,y=0,即-2≤y≤2,函数有最大值2,最小值-2.
误解:列表如下:
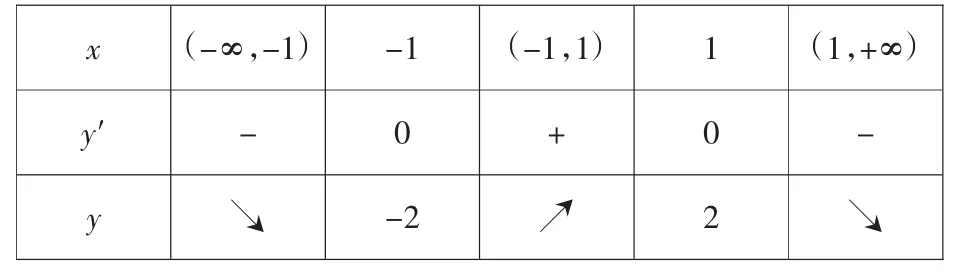
x (-∞,-1) -1 (-1,1) 1 (1,+∞)y′ - 0 + 0 -y↘-2↗2↘
因为函数的定义域为R,则函数的图像大致如图1,

故函数无最值.
评注:要注意当x→+∞,-∞时,函数的极限值,否则很容易认为函数无最值.实际上函数在x→+∞,-∞时的函数值是介于-2到2之间的,所以函数有最大值2,最小值-2.

