运用数形思想 巧解数学问题

☉江苏省盐城高等师范学校 沈 红

数形结合思想能把抽象的知识、数量关系与直观的图形以及位置关系结合起来，通过“由形化数”或“由数化形”，进行“数形转换”，可以将复杂问题简单化，抽象问题具体化，从而起到巧解数学问题的目的.下面，笔者结合自己教学实践经验，谈几点对运用数形结合思想，巧解数学问题的认识和看法，以供读者参考.

一、运用数形结合思想，巧妙解决代数问题

数形结合思想，大致分为两种情况：一是以数解形；二是以形助数.往往是通过精确的数来阐明形的某些属性，也可以通过形的几何直观性，来说明数之间的某种关系，进而不断揭示数学解题方法或策略.在教学中，有些代数问题，从直观去分析，寻求解决问题的突破口或解题途径，不易发现，使同学们不易走出困境.但我们如果构造几何图形，这样就非常容易使同学们发现解题的途径，使问题解决变的柳暗花明.

（1）若同时满足①、②的x值也满足③，求m的取值范围；

（2）若满足③的x值至少满足①和②中的一个，求m的取值范围.

解析：同学们根据已有知识，在下面热烈讨论，他们思考得出：该问题涉及整式、分式不等式和含绝对值不等式的知识，个人认为关键弄清同时满足①、②的x值满足③的充要条件是：③对应的方程的两根分别在区间（-∞，0）和［3，+∞）内.但要进行解决，需要把它们转化成图形，这样使问题不难化解，从中找到突破口，使问题迎刃而解.

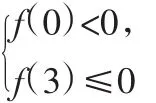
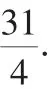
二、运用数形结合思想，巧妙解决三角问题

众所周知，三角函数变换问题蕴含着丰富的几何图形.如果把三角函数的问题融于几何图形之中，把数（量）与图形有机地结合起来，进行讨论、分析、研究，这样就能有效地促进同学们从抽象复杂的三角函数关系，经过几何图形观察，从中直观地发现问题解决的途径，达到事半功倍的效果.

分析：本案例是和差化积问题，通过三角函数公式，进行逐步化简，难度并不大，但我们利用单位圆进行问题转化，使问题解决显得独到好处，同学们在下面很快得出下列解法.

三、运用数形结合思想，巧妙解决几何问题

在教学中，我们要经常把几何问题代数化，去借助解方程（组）、不等式（组）、向量坐标等运算，来引导学生确定图形关系，去探讨解决问题的方法.所以，首先，我们要给学生梳理所学数学知识和数学方法；其次，要引导学生挖掘教材中隐藏的数学思想方法；第三，要把分析问题和解决问题的策略、方式、方法教给学生.同时要让同学们得到一定的训练，感受到其中的学习乐趣.

例3已知正方形ABCD边长为1，P是平面内任一点，求f（P）=PA+PB+PC+PD的最小值.

解析：如图2，建立坐标系，则A（0，0），B（1，0），C（1，1），D（0，1），设P（x，y），则：

由其特征，可用复数法解决该题. 设z1=x+yi，z2=x+（1-y）i，z3=（1-x）+（1-y）i，z4=（1-x）+yi，中，当且仅当x=y=时等号成立.f（P）的最小值为2