2012年高考数学江苏卷解析几何题别解
2012-08-27 02:55:22江西省赣县中学南校区朱红喜
中学数学杂志 2012年17期
☉江西省赣县中学南校区 朱红喜
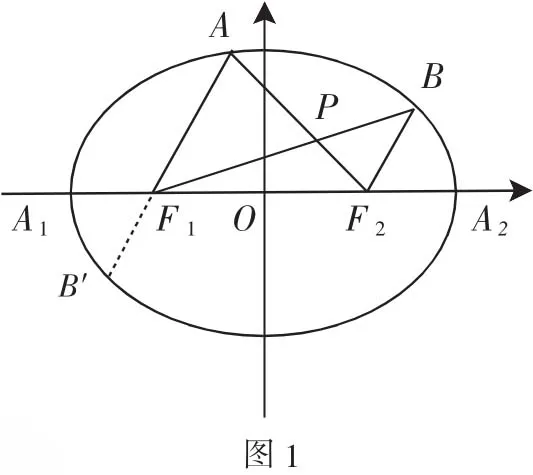
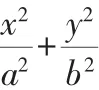
(1)求椭圆的方程;
(2)设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.
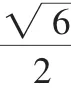
(ii)求证:PF1+PF2是定值.
(2)(i)如图1,设点B关于原点O的对称点为B′,连接F1B′,则四边形BF1B′F2为平行四边形.由AF1平行BF2,得A、F1、B′三点共线.
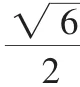
解法1:设A(x1,y1),B′(x2,y2).由椭圆的焦半径公式知
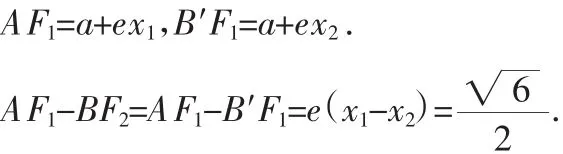
故x1-x2=,也因此知AB′的斜率存在且大于0.
设其斜率为k,则AB′的方程为y=k(x+1).
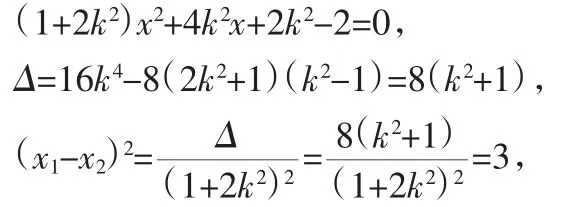
整理得12k4+4k2-5=0,

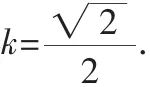
解法2: 设F1为极点,F1F2所在直线为极轴,∠F2F1A=θ,AF1=ρ1,B′F1=ρ2,则由圆锥曲线的统一极坐标方程得
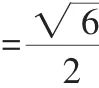
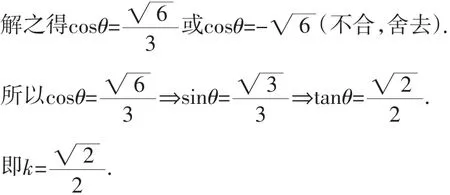
(2)(ii)解法1:由(2)(i)中解法2中的圆锥曲线统一极坐标方程,
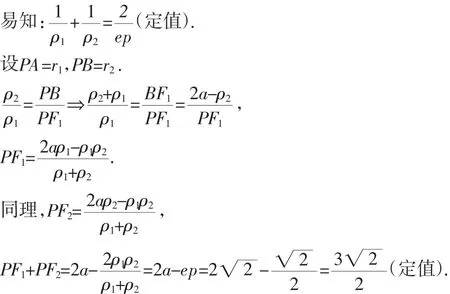
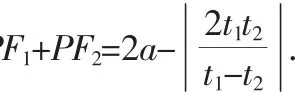
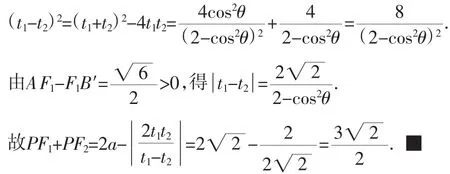
猜你喜欢
中等数学(2021年1期)2021-07-23 01:41:00
河北理科教学研究(2020年1期)2020-07-24 08:14:26
大众投资指南(2019年6期)2019-05-15 10:44:02
中学数学研究(广东)(2018年23期)2018-03-05 07:54:34
高中生·天天向上(2016年8期)2016-11-22 09:22:46
中学生数理化·高三版(2015年7期)2015-07-06 08:32:55
军事文摘·科学少年(2015年2期)2015-01-26 14:43:32
—— 对极轴(下)
天文爱好者(2014年1期)2014-10-11 00:42:20
天文研究与技术(2010年3期)2010-01-25 09:24:22
卫星电视与宽带多媒体(2009年10期)2009-07-03 04:24:10

