含有全称量词、存在量词的不等式成立问题的转化策略
2012-08-27 02:42湖北大学附属中学
中学数学杂志 2012年17期
☉湖北大学附属中学 李 俊
函数的最值以及含参数的函数的单调性与不等式恒成立的结合一直是高考命题的热点,特别是课改教材中引入了全称量词、存在量词等知识点之后,这一热点有持续高热之势.由于全称量词与存在量词的差异,对不等式两侧函数最值的要求也体现出了差异,以下给出有关全称量词、存在量词的不等式问题的转化策略.
(1)∀x1∈[m,n],∀x2∈[a,b],(fx1)≥g(x)2成立,则(fx)min≥g(x)max;
(2)∀x1∈[m,n],∃x2∈[a,b],f(x1)≥g(x2)成立,则f(x)min≥g(x)min;
(3)∃x1∈[m,n],∃x2∈[a,b],f(x1)≥g(x2)成立,则f(x)max≥g(x)min;
(4)∃x1∈[m,n],∀x2∈[a,b],f(x1)≥g(x2)成立,则f(x)max≥g(x)max;
(5)∀x0∈[m,n],f(x0)≥g(x0)成立,则[f(x)-g(x)]min≥0;
(6)∃x0∈[m,n],f(x0)≥g(x0)成立,则[f(x)-g(x)]max≥0.
下面用一个例子来说明以上6种情况的处理.

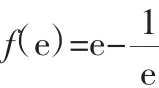
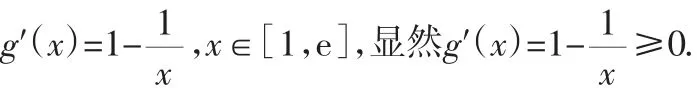
所以g(x)在[1,e]上单调递增.





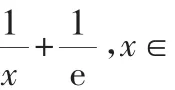


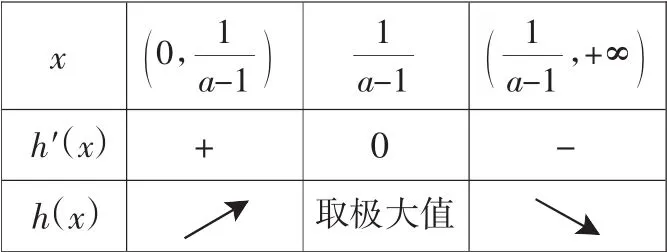



综合①②可知,满足条件的a的范围为[0,1].
猜你喜欢
中国脑血管病杂志(2022年4期)2022-11-10
中国脑血管病杂志(2022年3期)2022-10-03
中国脑血管病杂志(2022年2期)2022-09-01
江苏教育(2021年54期)2021-08-31
中小学校长(2021年7期)2021-08-21
新世纪智能(数学备考)(2020年9期)2021-01-04
小天使·一年级语数英综合(2020年3期)2020-12-16
学生天地(2020年24期)2020-06-09
中国脑血管病杂志(2019年4期)2019-10-29
小学生作文(低年级适用)(2019年10期)2019-10-28

