注重一题多解提升解题能力
☉江苏省南通市通州区石港中学 何永峰
同学们知道,所谓一题多解,就是指从各种不同的角度,运用不同的思维方法去解决同一个问题.由于一题多解所涉及的定理、性质比单一解题的面更广,方法更灵活多变,有时甚至是奇离巧合,曲径通幽,因此,一题多解不仅能锻炼解题的基本技能,而且可以有效地发展逻辑思维能力,全面提高分析问题和解决问题的能力.
解题方法丰富,培养多解能力,积累一题多解的经验,不存在什么秘诀,全凭持之以恒的勤奋探索,及时归纳、小结和加强训练.通过一题多解,可以加深对基本概念、性质、公式和定理的理解,并能从中筛选出最佳解法.
一、牢固掌握“双基”
“双基”即基础知识和基本技能,它是解题的基础,而熟练掌握“双基”,则是获得一题多解的前提条件.
解决问题的多种思路、方法与技巧来源于准确地掌握基础知识和基本技能.要准确理解和运用数学概念,牢固记忆和灵活运用定理、公式等基础知识,还要对题目的特点进行认真地分析,对有关图形进行细致地观察,将涉及到的有关基础知识进行有机的联想.基础知识掌握得不准确,解题过程就会漏洞百出.因此,在平常的学习中,首先要重视基础知识的学习,其次要重视知识链的归纳和完善,掌握解题依据.
对高三数学复习课来说,教师应根据大纲要求、教材的知识点及考纲的基本要点,结合近几年高考试题越来越重视学生的适应应用能力考查等特点,进一步明确教学目标与复习要求.通过对历年高考试题的分析,在复习中不能拘泥于课本习题,搞毫无新意的机械照搬或简单重复,也不能脱离书本,搞题海战术,而应着力于课本习题的潜在功能的挖掘,使学生的复习有更大的收获.在复习课中,应用一题多解的训练,可以牵动多面的知识和技能,对数学思想的渗透、发散思维的培养有较大的作用,是培养解题能力的良好方法.
二、注重观察、联想、转化
解题时注意观察、联想和转化,对开拓解题思路,探索一题多解的途径,提高解题能力,有着十分重要的作用.
观察,是审题、解题过程中重要的一环.通过观察,全面理解和掌握题目的条件和结论.具体来说,它包含如下两个方面:第一,搞清题中的条件和结论,弄懂题中所给概念和词语的含义,并对条件和结论进行分解;第二,对于条件和结论,应尽量使用数学符号来表示,有时还要画出草图,以助思考.通过观察,还要注意理解和掌握题目的特征,挖掘隐藏着的一些条件和启示.
联想,即从题目的特征包括问题的已知条件和结论联想有关知识.联想有:接近联想、类比联想、对比联想等.
转化,即解题的过程实际是连续的转化命题,直到所得结果成为已知为止.当然,是所求的结论更好.
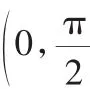
转化:原问题的求解转化为求cos(α+β)的值.
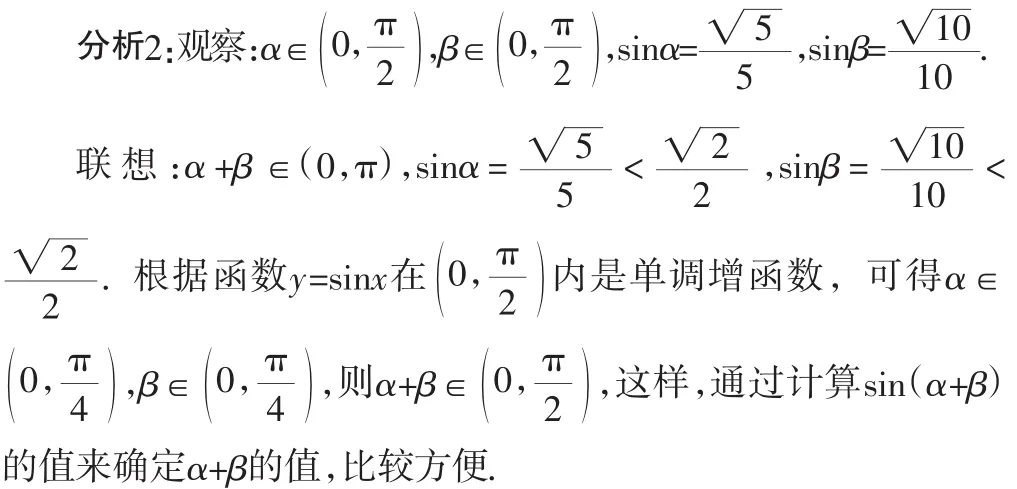
转化:原问题的求解转化为求sin(α+β)的值.
解决一个数学问题,往往是通过各种手段把它转化为已掌握的问题,用已掌握的方法加以解决.要转化就需要联想,联想已学过的有关知识和方法.
三、沟通各章节,要善于思考
从数学各章节之间的横向联系来看,数学各章节知识之间的内在联系,为我们开拓了一题多解的解题思路.只要我们能逐步养成将各部分知识融汇成一体地去分析、探究解题途径的习惯,那么我们的观察力和想象力就会不断提高,多解的思路就会一一涌现.比如在几何图形中通过作高、切线、弦心距等构造得到直角三角形,可以利用锐角三角函数知识,用三角方法来求解.又如对代数题,应尽可能立足于对条件及结论几何性质的分析,养成数形结合的解题习惯.
想法1:单纯从代数解法去考虑,将解析式移项、平方、整理成关于x的二次方程,就会找到利用判别式Δ≥0的解法,这种纯代数解法运算量较大,稍不小心就会前功尽弃.
想法2:用导数法来解,利用复合函数的求导公式,由于文科生对复合函数求导不作要求,他们虽然想到用导数法来解,但是一开始下手就会自己发明公式求错导数.
如果我们数形结合的联系平面几何、解析几何等的有关知识,多角度的去寻求解题途径,能得到简便的方法.
想法3:观察函数解析式的形式,联想解析几何中两点间的距离公式,建立直角坐标系,x轴上一动点P(x,0),使它到点A(0,2),B(1,3)的距离之和为最小.依据“异侧和最小,同侧差最大”去求解,所以只要求出B(1,3)关于x轴的对称点B′(1,-3)函数的最小值为
高中数学各章节之间的潜在联系,我们只要善于思考,就可以做到相互渗透、相互转化.所以平时要注重多角度、多方位思考问题,深入细致的观察,挖掘各章节知识的联系,提高学生分析问题和解决问题的能力.
四、掌握常用的解题方法和解题技巧
证明题常用方法为分析法、综合法、反证法、同一法、数学归纳法,其中数学归纳法作为江苏数学高考附加题、压轴题较多,学生只要掌握它的解题步骤:(1)验证当n=n0(n0是使命题成立的最小正整数)时,命题成立;(2)设n=k时,命题成立,进而证明n=k+1时命题也成立.由(1)(2)得原命题成立.由于附加题、压轴题较难,要拿满分比较困难,只要学生写出它的框架,10分的题目就可以拿到6至7分,也是很可观的.而配方法、待定系数法、换元法、解析法等重要的数学方法也是解题中常用的方法.对这些重要方法我们必须做到理论依据清楚,基本步骤明了,技巧手段娴熟,适用范围明确,并能根据题目的特征,迅速准确的选用合适的方法.
近几年江苏高考题中立体几何题,都考到了证明线面平行,我们知道要证线面平行有两个途径:一个是线线平行去证,一个是面面平行去证.其中用线线平行去证,我们就必须知道有哪些方法,用得较多的是线线平行的传递性,三角形中位线的平行以及平行四边形的对边平行等.而当我们看到比例式,就要马上想到相似三角形,多与三角形的重心的比例联系起来考,而这部分往往是学生薄弱的地方.所以我们要这样不断总结,就能不断提高.
因此,不断总结常用的解题方法,掌握解题技巧,为灵活运用所学知识,寻找多种解法打下了坚实的基础.做题不能只满足做出结果,每做完一题后,都要认真想一想,解题时用了哪些知识、方法和解题技巧,还有哪些解法,哪种方法最简便,解这类题有什么规律,应该注意什么问题,在此基础上若将条件加以改变,还能引出什么样的结论等等.当遇到问题时首先应该想到常规方法,当解题过程中遇到困难时要想到等价转化的思想,化繁为简.
高考场上的竞争就是解题能力的竞争,解题能力的强弱集中体现在解题思维的灵活性和解题方法的多样性上.如今的高考题入口很宽,常常可以用多种方法求解,从各种角度思考.如果思考缺乏灵活性就会因拘泥于某种思路而浪费时间,甚至失分;如果方法单一就会因墨守成规而误入歧途.所以在高三的复习课中要加强学生多渠道求解问题的能力.事实上,课本中许多习题由其蕴含的数学关系的复杂性和表现形式的多样性,为问题的多渠道求解提供了许多信息源.要打破原有的思维认识的禁锢,以教材的基本内容为基础,重新认识已经解决过的问题,以纵横交错的大跨度思维回顾教材知识体系,全方位、灵活寻找解题途径,调动所有的知识点,开创思维的新境界.

